Difference between revisions of "1978 IMO Problems/Problem 2"
(→Solution) |
(Undo revision 213854 by Elektrominds (talk)) (Tag: Undo) |
||
| (36 intermediate revisions by 2 users not shown) | |||
| Line 3: | Line 3: | ||
==Solution== | ==Solution== | ||
| − | Let <math>R</math> be the radius of the sphere. | + | |
| + | [[File:IMO_1978_P2a.png|400px]] | ||
| + | |||
| + | Let <math>R</math> be the radius of the given fixed sphere. | ||
Let point <math>O</math> be the center of the sphere. | Let point <math>O</math> be the center of the sphere. | ||
| Line 11: | Line 14: | ||
Let point <math>E</math> be the point where the line that passes through <math>OP</math> intersects the circle on the side nearest to point <math>A</math> | Let point <math>E</math> be the point where the line that passes through <math>OP</math> intersects the circle on the side nearest to point <math>A</math> | ||
| − | Let <math>\alpha=\ | + | Let <math>\alpha=\angle AOP,\;\beta=\angle BPD,\;\theta=\angle APE</math> |
We start the calculations as follows: | We start the calculations as follows: | ||
| Line 17: | Line 20: | ||
<math>\left| AB \right|= \left| PD \right|</math> | <math>\left| AB \right|= \left| PD \right|</math> | ||
| − | <math>\left| PD \right|^{2}=\left| PA \right|^{2}+\left| PB \right|^{2}</math> [Equation 1] | + | <math>\left| AB \right|^{2}=\left| PA \right|^{2}+\left| PB \right|^{2}</math> |
| + | |||
| + | Therefore, <math>\left| PD \right|^{2}=\left| PA \right|^{2}+\left| PB \right|^{2}</math> [Equation 1] | ||
Using law of cosines: | Using law of cosines: | ||
| − | <math>R^{2}=\left| OP \right|^{2} + \left| PB \right|^{2} - 2 \left| OP \right| \left| PB \right| cos (\ | + | <math>R^{2}=\left| OP \right|^{2} + \left| PB \right|^{2} - 2 \left| OP \right| \left| PB \right| cos (\angle OPB)</math> |
| − | <math>R^{2}=\left| OP \right|^{2} + \left| PB \right|^{2} - 2 \left| OP \right| \left| PB \right| cos (\frac{\pi}{2}-\theta)</math> | + | <math>R^{2}=\left| OP \right|^{2} + \left| PB \right|^{2} - 2 \left| OP \right| \left| PB \right| cos \left( \frac{\pi}{2}-\theta \right)</math> |
<math>R^{2}=\left| OP \right|^{2} + \left| PB \right|^{2} - 2 \left| OP \right| \left| PB \right| sin (\theta)</math> | <math>R^{2}=\left| OP \right|^{2} + \left| PB \right|^{2} - 2 \left| OP \right| \left| PB \right| sin (\theta)</math> | ||
| Line 32: | Line 37: | ||
<math>\left| PA \right|^{2} =R^{2}+\left| OP \right|^{2} - 2 \left| OP \right| R cos(\alpha)</math> | <math>\left| PA \right|^{2} =R^{2}+\left| OP \right|^{2} - 2 \left| OP \right| R cos(\alpha)</math> | ||
| + | |||
| + | Since <math>R cos(\alpha) = \left| PA \right| cos(\theta) + \left| OP\right|</math>, then | ||
<math>\left| PA \right|^{2} =R^{2}+\left| OP \right|^{2} - 2 \left| OP \right| \left[ \left| PA \right| cos(\theta) + \left| OP\right| \right]</math> | <math>\left| PA \right|^{2} =R^{2}+\left| OP \right|^{2} - 2 \left| OP \right| \left[ \left| PA \right| cos(\theta) + \left| OP\right| \right]</math> | ||
| Line 43: | Line 50: | ||
Now we apply the law of cosines again: | Now we apply the law of cosines again: | ||
| − | <math>\left| OD \right|^{2}=\left| OP \right|^{2}+\left| PD \right|^{2}-2\left| OP \right| \left| PD \right|cos(\ | + | <math>\left| OD \right|^{2}=\left| OP \right|^{2}+\left| PD \right|^{2}-2\left| OP \right| \left| PD \right|cos(\angle OPD)</math> |
| − | <math>\left| OD \right|^{2}=\left| OP \right|^{2}+\left| PD \right|^{2}-2\left| OP \right| \left| PD \right| cos(\ | + | <math>\left| OD \right|^{2}=\left| OP \right|^{2}+\left| PD \right|^{2}-2\left| OP \right| \left| PD \right| cos(\angle OPB+\angle BPD)</math> |
| − | <math>\left| OD \right|^{2}=\left| OP \right|^{2}+\left| PD \right|^{2}-2\left| OP \right| \left| PD \right| cos(\frac{\pi}{2}-\theta+\beta)</math> | + | <math>\left| OD \right|^{2}=\left| OP \right|^{2}+\left| PD \right|^{2}-2\left| OP \right| \left| PD \right| cos \left(\frac{\pi}{2}-\theta+\beta \right)</math> |
<math>\left| OD \right|^{2}=\left| OP \right|^{2}+\left| PD \right|^{2}-2\left| OP \right| \left| PD \right| sin(\theta-\beta)</math> | <math>\left| OD \right|^{2}=\left| OP \right|^{2}+\left| PD \right|^{2}-2\left| OP \right| \left| PD \right| sin(\theta-\beta)</math> | ||
| Line 57: | Line 64: | ||
<math>\left| OD \right|^{2}=\left| OP \right|^{2}+\left| PD \right|^{2}-2\left| OP \right| \left| PD \right| \left[\frac{\left| PB \right|}{\left| PD \right|}sin(\theta)-\frac{\left| PA \right|}{\left| PD \right|}cos(\theta) \right]</math> | <math>\left| OD \right|^{2}=\left| OP \right|^{2}+\left| PD \right|^{2}-2\left| OP \right| \left| PD \right| \left[\frac{\left| PB \right|}{\left| PD \right|}sin(\theta)-\frac{\left| PA \right|}{\left| PD \right|}cos(\theta) \right]</math> | ||
| − | <math>\left| OD \right|^{2}=\left| OP \right|^{2}+\left| PD \right|^{2}-2\left| OP \right| \left| | + | <math>\left| OD \right|^{2}=\left| OP \right|^{2}+\left| PD \right|^{2}-2\left| OP \right| \left[\left| PB \right|sin(\theta)-\left| PA \right|cos(\theta) \right]</math> [Equation 5] |
| + | |||
| + | Substituting [Equation 4] into [Equation 5] we get: | ||
| + | |||
| + | <math>\left| OD \right|^{2}=\left| OP \right|^{2}+2R^{2}-2\left| OP \right|^{2}+2\left| OP \right| \left[ \left| PB \right| sin(\theta) - \left| PA \right| cos(\theta) \right]-2\left| OP \right| \left[\left| PB \right|sin(\theta)-\left| PA \right|cos(\theta) \right]</math> | ||
| + | Notice that all of the terms with <math>\theta</math> cancel and thus we're left with: | ||
| + | <math>\left| OD \right|^{2}=2R^{2}-\left| OP \right|^{2}</math> regardless of <math>\theta</math>. [Equation 6] | ||
| + | Now we need to find <math>\left| PC \right|</math> | ||
| + | Since points <math>O</math>, <math>P</math>, and <math>C</math> are on the plane perpendicular to the plane with points <math>O</math>, <math>P</math>, and <math>A</math>, then these points lie on the big circle of the sphere. Therefore the distance <math>\left| PC \right|</math> can be found using the formula: | ||
| + | <math>R^{2}=\left| OP \right|^{2}+\left| PC \right|^2</math> | ||
| + | |||
| + | Solving for <math>\left| PC \right|^2</math> we get: | ||
| + | |||
| + | <math>\left| PC \right|^2=R^{2}-\left| OP \right|^{2}</math> [Equation 7] | ||
| + | |||
| + | Now we need to get <math>\left| OQ \right|^{2}</math> which will be using the formula: | ||
| + | |||
| + | <math>\left| OQ \right|^{2}=\left| OD \right|^{2}+\left| PC \right|^2</math> [Equation 8] | ||
| + | |||
| + | Substituting [Equation 6] and [Equation 7] into [Equation 8] we get: | ||
| + | |||
| + | <math>\left| OQ \right|^{2}=2R^{2}-\left| OP \right|^{2}+R^{2}-\left| OP \right|^{2}</math> | ||
| + | |||
| + | This results in: | ||
| + | |||
| + | <math>\left| OQ \right|^{2}=3R^{2}-2\left| OP \right|^{2}</math> | ||
| + | |||
| + | which is constant regardless of <math>\theta</math> and constant regardless of where points <math>A</math>, <math>B</math>, and <math>C</math> are located as long as they're still perpendicular to each other. | ||
| + | |||
| + | In space, this is a sphere with radius <math>\left| OQ \right|</math> which is equal to <math>\sqrt{3R^{2}-2\left| OP \right|^{2}}</math> | ||
| + | |||
| + | Therefore, the locus of vertex <math>Q</math> is a sphere of radius <math>\sqrt{3R^{2}-2\left| OP \right|^{2}}</math> with center at <math>O</math>, where <math>R</math> is the radius of the given sphere and <math>\left| OP \right|</math> the distance from the center of the given sphere to point <math>P</math> | ||
| + | |||
| + | ~ Tomas Diaz. orders@tomasdiaz.com | ||
{{alternate solutions}} | {{alternate solutions}} | ||
| − | == See Also == {{IMO box|year=1978|num-b=1|num-a=3}} | + | == See Also == |
| + | |||
| + | {{IMO box|year=1978|num-b=1|num-a=3}} | ||
| − | [[Category: | + | [[Category:Geometry Problems]] |
[[Category:Olympiad Geometry Problems]] | [[Category:Olympiad Geometry Problems]] | ||
Latest revision as of 12:00, 13 March 2024
Problem
We consider a fixed point ![]() in the interior of a fixed sphere
in the interior of a fixed sphere![]() We construct three segments
We construct three segments ![]() , perpendicular two by two
, perpendicular two by two![]() with the vertexes
with the vertexes ![]() on the sphere
on the sphere![]() We consider the vertex
We consider the vertex ![]() which is opposite to
which is opposite to ![]() in the parallelepiped (with right angles) with
in the parallelepiped (with right angles) with ![]() as edges
as edges![]() Find the locus of the point
Find the locus of the point ![]() when
when ![]() take all the positions compatible with our problem.
take all the positions compatible with our problem.
Solution
Let ![]() be the radius of the given fixed sphere.
be the radius of the given fixed sphere.
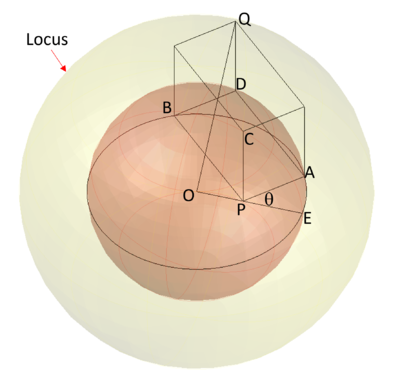
Let point ![]() be the center of the sphere.
be the center of the sphere.
Let point ![]() be the 4th vertex of the face of the parallelepiped that contains points
be the 4th vertex of the face of the parallelepiped that contains points ![]() ,
, ![]() , and
, and ![]() .
.
Let point ![]() be the point where the line that passes through
be the point where the line that passes through ![]() intersects the circle on the side nearest to point
intersects the circle on the side nearest to point ![]()
Let ![]()
We start the calculations as follows:
![]()
![]()
Therefore, ![]() [Equation 1]
[Equation 1]
Using law of cosines:
![]()
![]()
![]()
![]() [Equation 2]
[Equation 2]
Using law of cosines again we also get:
![]()
Since ![]() , then
, then
![]()
![]() [Equation 3]
[Equation 3]
Substituting [Equation 2] and [Equation 3] into [Equation 1] we get:
![]() [Equation 4]
[Equation 4]
Now we apply the law of cosines again:
![]()
![]()
![]()
![]()
![]()
Since, ![]() and
and ![]() then,
then,
![]()
![]() [Equation 5]
[Equation 5]
Substituting [Equation 4] into [Equation 5] we get:
![]()
Notice that all of the terms with ![]() cancel and thus we're left with:
cancel and thus we're left with:
![]() regardless of
regardless of ![]() . [Equation 6]
. [Equation 6]
Now we need to find ![]()
Since points ![]() ,
, ![]() , and
, and ![]() are on the plane perpendicular to the plane with points
are on the plane perpendicular to the plane with points ![]() ,
, ![]() , and
, and ![]() , then these points lie on the big circle of the sphere. Therefore the distance
, then these points lie on the big circle of the sphere. Therefore the distance ![]() can be found using the formula:
can be found using the formula:
![]()
Solving for ![]() we get:
we get:
![]() [Equation 7]
[Equation 7]
Now we need to get ![]() which will be using the formula:
which will be using the formula:
![]() [Equation 8]
[Equation 8]
Substituting [Equation 6] and [Equation 7] into [Equation 8] we get:
![]()
This results in:
![]()
which is constant regardless of ![]() and constant regardless of where points
and constant regardless of where points ![]() ,
, ![]() , and
, and ![]() are located as long as they're still perpendicular to each other.
are located as long as they're still perpendicular to each other.
In space, this is a sphere with radius ![]() which is equal to
which is equal to ![]()
Therefore, the locus of vertex ![]() is a sphere of radius
is a sphere of radius ![]() with center at
with center at ![]() , where
, where ![]() is the radius of the given sphere and
is the radius of the given sphere and ![]() the distance from the center of the given sphere to point
the distance from the center of the given sphere to point ![]()
~ Tomas Diaz. orders@tomasdiaz.com
Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.
See Also
| 1978 IMO (Problems) • Resources | ||
| Preceded by Problem 1 |
1 • 2 • 3 • 4 • 5 • 6 | Followed by Problem 3 |
| All IMO Problems and Solutions | ||