Difference between revisions of "Barycentric coordinates"
(→Points on bisectors) |
(→Small Pascal's theorem) |
||
| (8 intermediate revisions by 2 users not shown) | |||
| Line 12: | Line 12: | ||
<i><b>Notation</b></i> | <i><b>Notation</b></i> | ||
| − | Let the triangle <math>\triangle ABC</math> be a given triangle, <math>a, b, c</math> be the lengths of <math>BC, AC, AB, \angle A = \alpha, \angle B = \beta, \angle C = \gamma.</math> | + | Let the triangle <math>\triangle ABC</math> be a given triangle, <math>a, b, c,</math> be the lengths of <math>BC, AC, AB, \angle A = \alpha, \angle B = \beta, \angle C = \gamma.</math> |
We use the following Conway symbols: | We use the following Conway symbols: | ||
| Line 320: | Line 320: | ||
<cmath>A= (1:0:0), B= (0:1:0), C= (0:0:1), I=(a:b:c),</cmath> | <cmath>A= (1:0:0), B= (0:1:0), C= (0:0:1), I=(a:b:c),</cmath> | ||
<cmath>A'= (0:b:c), B'= (a:0:c), C'= (a:b:0), M = (1:1:0).</cmath> | <cmath>A'= (0:b:c), B'= (a:0:c), C'= (a:b:0), M = (1:1:0).</cmath> | ||
| − | + | Line <math>AA'</math> is <math>cy=bz,</math> line <math>BB'</math> is <math>cx=az,</math> line <math>CC'</math> is <math>bx=ay.</math> | |
| − | < | ||
| − | < | ||
| − | < | ||
| − | < | ||
| − | + | Circle <math>\Omega</math> is <math>xyc^2 + xzb^2 + yza^2 = 0.</math> | |
| − | + | <cmath> D = \Omega \cap AA', D= \left( - \frac {a^2}{b+c}:b:c \right), E = \Omega \cap BB', E = \left(a: - \frac {b^2}{a+c}:c \right),</cmath> | |
| + | <cmath>F = \Omega \cap CC', F = \left(a:b: - \frac {c^2}{a+b} \right), K = BE \cap A'C', K = (a : 2b : c)</cmath> | ||
| − | Line <math> | + | Line <math>DF</math> is <math>x \frac {b+c}{a} +y + z\frac {a+b}{c} = 0. </math> |
| − | |||
| − | Point <math> | + | Point <math>L = BE \cap DF, L = (a : a+2b+c : c).</math> |
| + | Line <math>FM</math> is <math>x = y + z \frac {b^2 - a^2}{c^2}.</math> | ||
| + | |||
| + | Point <math>G = AD \cap FM, G = \left( b+ \frac {b^2-a^2}{c} :b: c \right).</math> | ||
| + | |||
| + | Point <math>H = BE \cap FM, H = \left( a: a - \frac {b^2-a^2}{c} : c \right).</math> | ||
| + | [[File:Bisector division A.png|400px|right]] | ||
Some simple formulas: | Some simple formulas: | ||
<cmath>\frac {FM}{GM} = \frac {b+c-a}{a+b-c}; \frac {FM}{FG} = \frac {b+c-a}{2b};</cmath> | <cmath>\frac {FM}{GM} = \frac {b+c-a}{a+b-c}; \frac {FM}{FG} = \frac {b+c-a}{2b};</cmath> | ||
| Line 339: | Line 341: | ||
<cmath>\frac {EH}{B'E} = \frac {a(a+c)}{b^2}; \frac {IH}{B'E} = \frac {|a-b|(a+c)}{b^2};</cmath> | <cmath>\frac {EH}{B'E} = \frac {a(a+c)}{b^2}; \frac {IH}{B'E} = \frac {|a-b|(a+c)}{b^2};</cmath> | ||
<cmath>\frac {B'I}{IE} = 1 - \frac {b}{a+c}; \frac {IB}{2} = IL = BL.</cmath> | <cmath>\frac {B'I}{IE} = 1 - \frac {b}{a+c}; \frac {IB}{2} = IL = BL.</cmath> | ||
| − | Circumcenter <math>O \in FM | + | Circumcenter <math>O \in FM , O = \left( a^2(b^2+c^2 -a^2) : b^2(a^2 + c^2 – b^2) : c^2(a^2 + b^2 - c^2) \right).</math> |
| − | Tangent <math>BN | + | Tangent <math>BN</math> is <math>c^2 x + a^2 z = 0.</math> |
| − | Line <math>NI || AC | + | Line <math>NI || AC</math> is <math>\left( \frac {b}{a+c} = \frac{y}{x+z} \right).</math> |
| − | <cmath>N = BN \cap IN | + | <cmath>N = BN \cap IN, N = (a^2 : b(a - c) : -c^2).</cmath> |
<cmath>BN = IN = \frac {abc}{|a-c|(a+b+c)}.</cmath> | <cmath>BN = IN = \frac {abc}{|a-c|(a+b+c)}.</cmath> | ||
<cmath>\frac{HO}{BO} = \frac {|a-c|}{b}; \frac{GO}{BO} = \frac {|b-c|}{a}.</cmath> | <cmath>\frac{HO}{BO} = \frac {|a-c|}{b}; \frac{GO}{BO} = \frac {|b-c|}{a}.</cmath> | ||
| Line 352: | Line 354: | ||
<cmath>\frac {IC'}{FC'} = \frac {a+b-c}{c}; \frac {IA'}{DA'} = \frac {b+c-a}{a};</cmath> | <cmath>\frac {IC'}{FC'} = \frac {a+b-c}{c}; \frac {IA'}{DA'} = \frac {b+c-a}{a};</cmath> | ||
<cmath>\frac {ND}{NF} = \frac {a(a+b-c)}{c(b+c-a)}.</cmath> | <cmath>\frac {ND}{NF} = \frac {a(a+b-c)}{c(b+c-a)}.</cmath> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==Small Pascal's theorem== | ||
| + | [[File:PascalS Lemoine.png|390px|right]] | ||
| + | [[File:Pascal S Lemoine E.png|390px|right]] | ||
| + | |||
| + | Let <math>\triangle ABC</math> and point <math>P</math> be given. Let <math>\Omega</math> be the circumcircle of <math>\triangle ABC,</math> | ||
| + | <cmath>A' = AP \cap \Omega, B' = BP \cap \Omega, C' = CP \cap \Omega.</cmath> | ||
| + | Let the tangent line to <math>\Omega</math> at point <math>A</math> cross line <math> B'C'</math> at point <math>D.</math> Similarly denote points <math>E</math> and <math>F.</math> | ||
| + | |||
| + | Prove that the points <math>D, E</math> and <math>F</math> are collinear. | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | 1. Simplest case, <math>P</math> is the Lemoine point, <math>P = L = (a^2 : b^2 : c^2).</math> | ||
| + | |||
| + | The equation of <math>\Omega</math> is <math> xyc^2 + xzb^2 + yza^2 = 0.</math> | ||
| + | |||
| + | Line <math>AP</math> is <math>k = 0, l y_P + m z_P = 0 \implies y c^2 - z b^2 = 0 \implies </math> | ||
| + | <cmath>A' = \left(-\frac{a^2}{2} : b^2 : c^2 \right), B' = \left(a^2 : -\frac{b^2}{2} : c^2 \right), C' = \left(a^2 : b^2 : -\frac{c^2}{2} \right).</cmath> | ||
| + | The line <math>B'C'</math> is <math>\frac{x}{2a^2} - \frac{y}{b^2} - \frac{z}{c^2} = 0 \implies D = \left( 0 : b^2 : - c^2 \right).</math> | ||
| + | |||
| + | Similarly, <math>E = ( a^2 : 0 : - c^2), F = (a^2 : - b^2 : 0).</math> | ||
| + | |||
| + | The line <math>DEF</math> is <math>\frac {x}{a^2} + \frac {y}{b^2} + \frac {z}{c^2} = 0.</math> | ||
| + | |||
| + | 2. Simple case, <math>P</math> is one of the external Lemoine point, <math>P = L' = (a^2 : - b^2 : c^2).</math> | ||
| + | |||
| + | This point is the crosspoint of the tangent lines to <math>\Omega</math> in points <math>A</math> and <math>C,</math> so | ||
| + | <cmath>A' = A, C' = C, B' = \left (a^2 : -\frac{b^2}{2} : c^2 \right ).</cmath> | ||
| + | The line <math>B'C'</math> is <math>b^2 x + 2y a^2 = 0 \implies D = \left( 2a^2 : -b^2 : c^2 \right).</math> | ||
| + | |||
| + | Similarly, <math>E = ( a^2 : 0 : - c^2), F = (a^2 : - b^2 : 2c^2).</math> | ||
| + | |||
| + | The line <math>DEF</math> is <math>\frac {x}{a^2} + \frac {3y}{b^2} + \frac {z}{c^2} = 0.</math> | ||
| + | |||
| + | Similarly, if <math>P = (-a^2 : b^2 : c^2),</math> then the line <math>DEF</math> is <math>\frac {3x}{a^2} + \frac {y}{b^2} + \frac {z}{c^2} = 0.</math> | ||
| + | |||
| + | If <math>P = (a^2 : b^2 : -c^2),</math> then the line <math>DEF</math> is <math>\frac {x}{a^2} + \frac {y}{b^2} + \frac {3z}{c^2} = 0.</math> | ||
| + | |||
| + | These three lines intersect in pairs at points <math>D, E,</math> and <math>F</math> of the line of case 1. | ||
| + | |||
| + | 3. Common case. Denote the coordinates of the point <math>P = (x_P : y_P : z_P).</math> The equation of <math>\Omega</math> is <math> xyc^2 + xzb^2 + yza^2 = 0.</math> | ||
| + | |||
| + | Line <math>AP</math> is <math>l z_P + m y_P = 0 \implies A' = \left( \frac{-y_P \cdot z_P a^2}{y_P c^2 + z_P b^2} : y_P :z_P \right ).</math> | ||
| + | |||
| + | Similarly, <math>B' = \left (x_P : \frac{-x_P \cdot z_P b^2}{x_P c^2 + z_P a^2} : z_P \right ), C' = \left (x_P : y_P : \frac{-x_P \cdot y_P c^2}{x_P b^2 + y_P a^2} \right ).</math> | ||
| + | |||
| + | The tangent line <math>l_A</math> to <math>\Omega</math> at <math>A</math> is <math>yC^2 +zb^2=0.</math> | ||
| + | |||
| + | The line <math>B'C'</math> is <math>\frac{y_P \cdot z_P a^2}{x_P} x - (x_P \cdot c^2 + z_P a^2)y - (x_P b^2 +y_Pa^2)z = 0.</math> | ||
| + | |||
| + | <math>D = l_A \cap B'C' = \left( x_P (y_P c^2 - z_P b^2) : -y_P \cdot z_P b^2 : y_P \cdot z_P c^2 \right).</math> | ||
| + | |||
| + | Similarly, <math>E = l_B \cap A'C' = \left( x_P z_P a^2 : -y_P (x_P c^2 - z_P a^2) : -x_P \cdot z_P c^2 \right).</math> | ||
| + | <cmath>F = l_C \cap A'B' = \left( x_P y_P a^2 : -x_P y_P b^2 : z_P (y_P a^2 - x_P b^2) \right).</cmath> | ||
| + | The line <math>DEF</math> is <cmath> \frac {x}{x_P} (-\frac {a^2}{x_P} + \frac {b^2}{y_P} + \frac {c^2}{z_P}) + \frac {y}{y_P} (\frac {a^2}{x_P} - \frac {b^2}{y_P} + \frac {c^2}{z_P}) +\frac {z}{z_P} (\frac {a^2}{x_P} + \frac {b^2}{y_P} - \frac {c^2}{z_P}) = 0.</cmath> | ||
'''vladimir.shelomovskii@gmail.com, vvsss''' | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
Revision as of 14:12, 6 July 2024
This can be used in mass points. http://mathworld.wolfram.com/BarycentricCoordinates.html This article is a stub. Help us out by expanding it.
Barycentric coordinates are triples of numbers ![]() corresponding to masses placed at the vertices of a reference triangle
corresponding to masses placed at the vertices of a reference triangle ![]() . These masses then determine a point
. These masses then determine a point ![]() , which is the geometric centroid of the three masses and is identified with coordinates
, which is the geometric centroid of the three masses and is identified with coordinates ![]() . The vertices of the triangle are given by
. The vertices of the triangle are given by ![]() ,
, ![]() , and
, and ![]() . Barycentric coordinates were discovered by Möbius in 1827 (Coxeter 1969, p. 217; Fauvel et al. 1993).
. Barycentric coordinates were discovered by Möbius in 1827 (Coxeter 1969, p. 217; Fauvel et al. 1993).
The Central NC Math Group published a lecture concerning this topic at https://www.youtube.com/watch?v=KQim7-wrwL0 if you would like to view it.
Contents
Useful formulas
Notation
Let the triangle ![]() be a given triangle,
be a given triangle, ![]() be the lengths of
be the lengths of ![]()
We use the following Conway symbols:
![]() is semiperimeter,
is semiperimeter, ![]() is twice the area of
is twice the area of ![]()
![]() where
where ![]() is the inradius,
is the inradius, ![]() is the circumradius,
is the circumradius,
![]() is the cosine of the Brocard angle,
is the cosine of the Brocard angle,
![]()
Main
For any point in the plane ![]() there are barycentric coordinates(BC):
there are barycentric coordinates(BC): ![]()
![]()
![]() The normalized (absolute) barycentric coordinates NBC satisfy the condition
The normalized (absolute) barycentric coordinates NBC satisfy the condition ![]() they are uniquely determined:
they are uniquely determined:
![]()
![]() Triangle vertices
Triangle vertices ![]()
The barycentric coordinates of a point do not change under an affine transformation.
Lines
The straight line in barycentric coordinates (BC) is given by the equation ![]()
The lines given in the BC by the equations ![]() and
and ![]() intersect at the point
intersect at the point
![]()
These lines are parallel iff ![]()
The sideline ![]() contains the points
contains the points ![]() its equation is
its equation is ![]()
The line ![]() has equation
has equation ![]() it intersects the sideline
it intersects the sideline ![]() at the point
at the point ![]()
Iff ![]() then
then ![]()
Let NBC of points ![]() and
and ![]() be
be ![]()
Then the square of distance ![]()
![]() The equation of bisector of
The equation of bisector of ![]() is:
is:
![]() Nagel line :
Nagel line : ![]()
Circles
Any circle is given by an equation of the form ![]()
Circumcircle contains the points ![]() the equation of this circle:
the equation of this circle: ![]()
The incircle contains the tangent points of the incircle with the sides:
![]()
The equation of the incircle is
![]() where
where ![]()
The radical axis of two circles given by equations of this form is:
![]() Conjugate
Conjugate
The point ![]() is isotomically conjugate with respect to
is isotomically conjugate with respect to ![]() with the point
with the point ![]()
The point ![]() is isogonally conjugate with respect to
is isogonally conjugate with respect to ![]() with the point
with the point ![]()
The point ![]() is isocircular conjugate with respect to
is isocircular conjugate with respect to ![]() with the point
with the point ![]()
Triangle centers
The median ![]() centroid is
centroid is ![]()
The simmedian point ![]() is isogonally conjugate with respect to
is isogonally conjugate with respect to ![]() with the point
with the point ![]()
The bisector ![]() the incenter is
the incenter is ![]()
The excenters are ![]()
The circumcenter ![]() lies at the intersection of the bisectors
lies at the intersection of the bisectors ![]() and
and ![]() its BC coordinates
its BC coordinates ![]()
The orthocenter ![]() is isogonally conjugate with respect to
is isogonally conjugate with respect to ![]() with the point
with the point ![]()
Let Nagel point ![]() lies at line
lies at line ![]()
The Gergonne point is the isotomic conjugate of the Nagel point, so ![]()
vladimir.shelomovskii@gmail.com, vvsss
Product of isogonal segments
Let triangle ![]() the circumcircle
the circumcircle ![]() and isogonals
and isogonals ![]() and
and ![]() of the
of the ![]() be given.
Let point
be given.
Let point ![]() and
and ![]() be the isogonal conjugate of a point
be the isogonal conjugate of a point ![]() and
and ![]() with respect to
with respect to ![]() Prove that
Prove that ![]()
Proof
We fixed ![]() and the point
and the point ![]() So isogonal
So isogonal ![]() is fixed.
is fixed.
Denote ![]()
We need to prove that ![]() do not depends from
do not depends from ![]()
Line ![]() has the equation
has the equation ![]()
To find the point ![]() we solve the equation:
we solve the equation: ![]()
![]() We use the formula for isogonal cobnjugate point and get
We use the formula for isogonal cobnjugate point and get
![]() and then
and then ![]()
To find the point ![]() we solve the equation:
we solve the equation: ![]()
![]() We calculate distances (using NBC) and get:
We calculate distances (using NBC) and get:
![]()
![]() where
where ![]() has sufficiently big formula.
has sufficiently big formula.
Therefore ![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Ratio of isogonal segments
Let triangle ![]() and point
and point ![]() be given.
Denote
be given.
Denote ![]() the isogonal conjugate of a point
the isogonal conjugate of a point ![]() with respect to
with respect to ![]()
![]() Prove that
Prove that ![]()
Proof
We use the formula for isogonal conjugate point and get ![]()
![]()
![]()
![]()
![]()
![]()
vladimir.shelomovskii@gmail.com, vvsss
Point on incircle
Let triangle ![]() be given. Denote the incircle
be given. Denote the incircle ![]() the incenter
the incenter ![]() , the Spieker center
, the Spieker center ![]()
Let ![]() be the point corresponding to the condition
be the point corresponding to the condition ![]() is symmetric
is symmetric ![]() with respect midpoint
with respect midpoint ![]()
Symilarly denote ![]()
Prove that point ![]() lies on
lies on ![]()
Proof
![]()
![]() We calculate distances (using NBC) and solve the system of equations:
We calculate distances (using NBC) and solve the system of equations:
![]()
We know one solution of this system (point D), so we get linear equation and get:
![]()
![]()
![]() Similarly
Similarly ![]() Therefore
Therefore ![]() We calculate the length of the segment
We calculate the length of the segment ![]() and get
and get ![]()
The author learned about the existence of such a point from Leonid Shatunov in August 2023.
vladimir.shelomovskii@gmail.com, vvsss
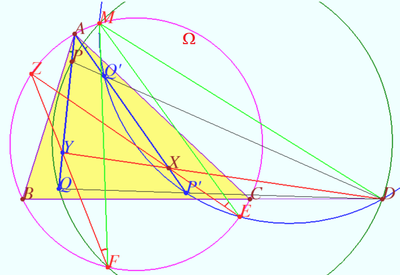
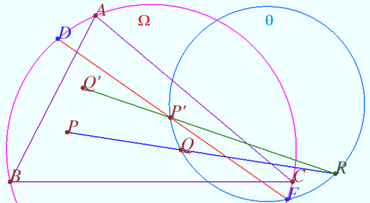
Crossing point
Let triangle ![]() and points
and points ![]() and
and ![]() be given. Let point
be given. Let point ![]() be the isogonal conjugate of a point
be the isogonal conjugate of a point ![]() with respect to a triangle
with respect to a triangle ![]() Let
Let ![]() be an arbitrary point at
be an arbitrary point at ![]()
![]() Prove that
Prove that ![]() lies on
lies on ![]()
This configuration can be used as a straight-line mechanism since it allows to create a mechanism that converts the rotational motion of a point Z to perfect straight-line motion of the X point or vice versa. Of course, we need to use the prismatic joint at the points ![]() and
and ![]()
Proof
We use the barycentric coordinates: ![]()
![]() We get the equations for some lines:
We get the equations for some lines:
Line ![]() is
is ![]()
line ![]() is
is ![]()
line ![]() is
is ![]()
line ![]() is
is ![]()
line ![]() is
is ![]()
We get the equations for some points:
point ![]() is
is ![]()
point ![]() is
is ![]()
point ![]() is
is ![]()
Any circle is given by an equation of the form ![]() We find the coefficients for the circles (these formulas are big), but can be used for calculations of the crossing points:
We find the coefficients for the circles (these formulas are big), but can be used for calculations of the crossing points:
![]()
![]() We get the equations for some lines
We get the equations for some lines ![]() and
and ![]() :
:
![]()
![]() We get the equation for the point
We get the equation for the point ![]()
![]() Let point
Let point ![]() be the isogonal conjugate of a point
be the isogonal conjugate of a point ![]() with respect to a triangle
with respect to a triangle ![]()
![]() The sum of coordinates is equal zero, so
The sum of coordinates is equal zero, so ![]() is in infinity, therefore the point
is in infinity, therefore the point ![]() lies on
lies on ![]()
vladimir.shelomovskii@gmail.com, vvsss
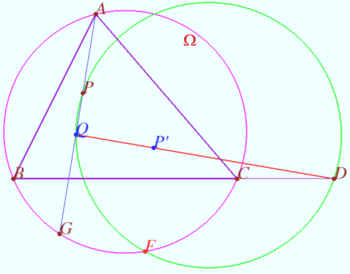
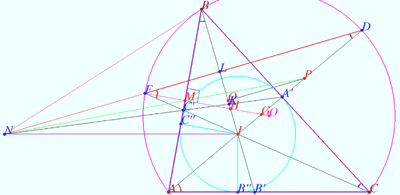
Fixed point on circumcircle
Let triangle ![]() point
point ![]() on circumcircle
on circumcircle ![]() and point
and point ![]() be given.
Point
be given.
Point ![]() lies on
lies on ![]() point
point ![]() be the isogonal conjugate of a point
be the isogonal conjugate of a point ![]() with respect to a triangle
with respect to a triangle ![]()
Prove that ![]() is fixed point and not depends from position of
is fixed point and not depends from position of ![]()
Proof
Denote the coordinates of the points ![]()
![]()
![]()
![]() The line
The line ![]() is
is ![]()
The line ![]() is
is ![]()
![]() We find the circle
We find the circle ![]() and get the point
and get the point
![\[F =\left( \frac {a^2}{\frac {c^2}{z_D \cdot z_G} - \frac{b^2}{y_D \cdot y_G}} : y_G \cdot y_D : - z_G \cdot z_D \right).\]](http://latex.artofproblemsolving.com/a/5/d/a5d259e35346d42f2d09081f526a415652f99cbe.png)
![]() depends only from points
depends only from points ![]() and
and ![]()
vladimir.shelomovskii@gmail.com, vvsss
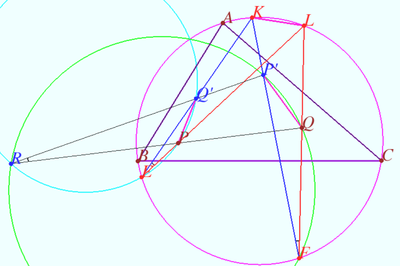
Two pare isogonal points
Let triangle ![]() and points
and points ![]() and
and ![]() (points do not lie on sidelines) be given.
(points do not lie on sidelines) be given.
Let point ![]() and
and ![]() be the isogonal conjugate of a point
be the isogonal conjugate of a point ![]() and
and ![]() with respect to a triangle
with respect to a triangle ![]()
Denote ![]()
Prove that ![]() and
and ![]() lies on
lies on ![]()
Proof
The line ![]() is
is
![]() The line
The line ![]() is
is
![]()
![]()
![]()
![]()
![]() Denote
Denote ![]() is the isogonal conjugate of a point
is the isogonal conjugate of a point ![]() with respect to
with respect to ![]()
![]()
![]() If we use NBC, we get
If we use NBC, we get ![]()
![\[L = EP \cap FQ = \left( \frac {1}{\frac {b^2} {x_Q y_P} - \frac {b^2} {x_P y_Q}+ \frac {c^2} {x_Q z_P}- \frac {c^2} {x_Q z_P}} : \frac {1}{\frac {a^2} {x_Q y_P} - \frac {a^2} {x_P y_Q}+ \frac {c^2} {z_Q y_P}- \frac {c^2} {y_Q z_P}} : \frac {1}{\frac {a^2} {x_Q z_P} - \frac {a^2} {x_P z_Q}+ \frac {b^2} {y_Q z_P}- \frac {b^2} {y_P z_Q}} \right).\]](http://latex.artofproblemsolving.com/b/a/f/baf8817822cfb7f7378ad045edd3c3ee8c5658a3.png)
![]() If we use NBC, we get
If we use NBC, we get ![]()
vladimir.shelomovskii@gmail.com, vvsss
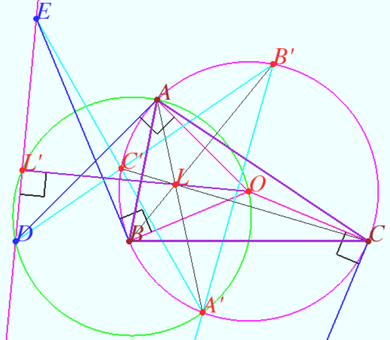
Collinearity for two pares of isogonal points
Let triangle ![]() and points
and points ![]() and
and ![]() be given. Let point
be given. Let point ![]() and
and ![]() be the isogonal conjugate of the points
be the isogonal conjugate of the points ![]() and
and ![]() with respect to a triangle
with respect to a triangle ![]()
Denote ![]() is the point isogonal conjugate to line
is the point isogonal conjugate to line ![]() with respect
with respect ![]() Isogonal_bijection_lines_and_points
Isogonal_bijection_lines_and_points
Prove that points ![]() and
and ![]() are collinear.
are collinear.
Proof
![]() After the simple calculations one can get:
After the simple calculations one can get:
![]()
![]()
![]() We use the normalized barycentric coordinates NBC and get line
We use the normalized barycentric coordinates NBC and get line ![]() in the form of:
in the form of:
![]()
![]()
![]() We check the condition of collinearity for points
We check the condition of collinearity for points ![]() and
and ![]() and finishing the proof.
and finishing the proof. ![]()
vladimir.shelomovskii@gmail.com, vvsss
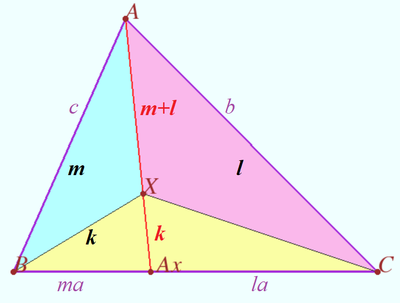
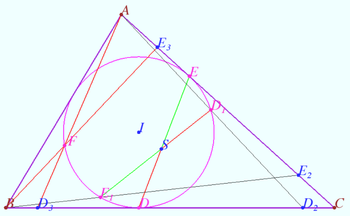
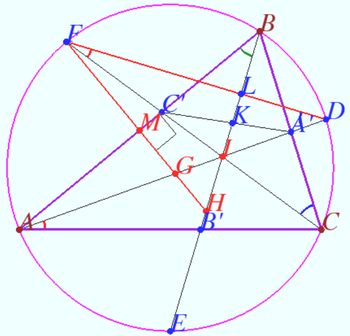
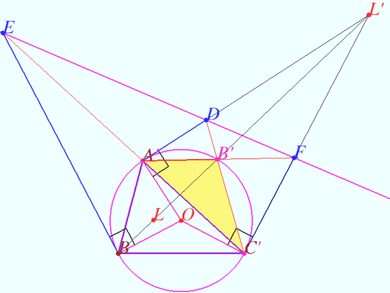
Points on bisectors
Let a triangle ![]() be given.
be given.
Let segments ![]() and
and ![]() be the bisectors of
be the bisectors of ![]()
The lines ![]() and
and ![]() meet circumcircle
meet circumcircle ![]() ) at points
) at points ![]() respectively.
respectively. ![]() is the midpoint
is the midpoint ![]() Denote
Denote ![]()
We will find barycentric coordinates of the points and length of the segments.
![]()
![]() Line
Line ![]() is
is ![]() line
line ![]() is
is ![]() line
line ![]() is
is ![]()
Circle ![]() is
is ![]()
![]()
![]()
Line ![]() is
is ![]()
Point ![]()
Line ![]() is
is ![]()
Point ![]()
Point ![]()
Some simple formulas:
![]()
![]()
![]()
![]() Circumcenter
Circumcenter ![]()
Tangent ![]() is
is ![]()
Line ![]() is
is ![]()
![]()
![]()
![]()
![]() is the midpoint
is the midpoint ![]()
![]()
![]()
![]()
![]()
vladimir.shelomovskii@gmail.com, vvsss
Small Pascal's theorem
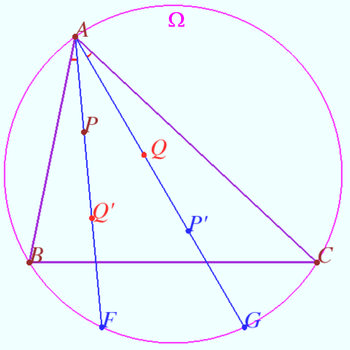
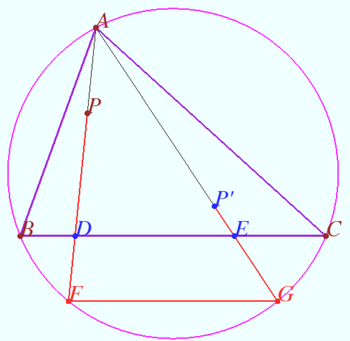
Let ![]() and point
and point ![]() be given. Let
be given. Let ![]() be the circumcircle of
be the circumcircle of ![]()
![]() Let the tangent line to
Let the tangent line to ![]() at point
at point ![]() cross line
cross line ![]() at point
at point ![]() Similarly denote points
Similarly denote points ![]() and
and ![]()
Prove that the points ![]() and
and ![]() are collinear.
are collinear.
Proof
1. Simplest case, ![]() is the Lemoine point,
is the Lemoine point, ![]()
The equation of ![]() is
is ![]()
Line ![]() is
is ![]()
![]() The line
The line ![]() is
is ![]()
Similarly, ![]()
The line ![]() is
is ![]()
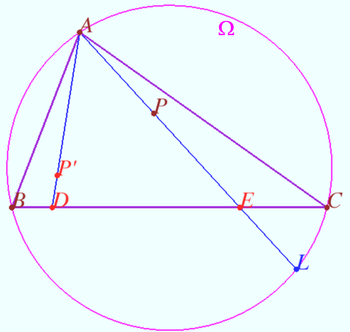
2. Simple case, ![]() is one of the external Lemoine point,
is one of the external Lemoine point, ![]()
This point is the crosspoint of the tangent lines to ![]() in points
in points ![]() and
and ![]() so
so
![]() The line
The line ![]() is
is ![]()
Similarly, ![]()
The line ![]() is
is ![]()
Similarly, if ![]() then the line
then the line ![]() is
is ![]()
If ![]() then the line
then the line ![]() is
is ![]()
These three lines intersect in pairs at points ![]() and
and ![]() of the line of case 1.
of the line of case 1.
3. Common case. Denote the coordinates of the point ![]() The equation of
The equation of ![]() is
is ![]()
Line ![]() is
is ![]()
Similarly, ![]()
The tangent line ![]() to
to ![]() at
at ![]() is
is ![]()
The line ![]() is
is ![]()
![]()
Similarly, ![]()
![]() The line
The line ![]() is
is ![]()
vladimir.shelomovskii@gmail.com, vvsss