Difference between revisions of "1997 PMWC Problems"
(deleted *enters* and added *spaces*) |
(tex/fmt) |
||
| Line 1: | Line 1: | ||
== Problem I1 == | == Problem I1 == | ||
| − | Evaluate 29 27 | + | Evaluate <math>29 \dfrac{27}{28} \times 27 \frac{14}{15}</math> |
[[1997 PMWC Problems/Problem I1|Solution]] | [[1997 PMWC Problems/Problem I1|Solution]] | ||
| Line 63: | Line 63: | ||
== Problem I11 == | == Problem I11 == | ||
| − | A rectangle ABCD is made up of five small congruent rectangles as shown in the given figure. Find the perimeter, in cm, of ABCD if its area is <math>6750 cm^2</math>. | + | A rectangle <math>ABCD</math> is made up of five small congruent rectangles as shown in the given figure. Find the perimeter, in cm, of <math>ABCD</math> if its area is <math>6750 \text{cm}^2</math>. |
[[Image:ABCD.gif]] | [[Image:ABCD.gif]] | ||
| Line 81: | Line 81: | ||
== Problem I13 == | == Problem I13 == | ||
| − | A truck moved from A to B at a speed of 50 km/h and returns from B to A at 70 km/h. It traveled 3 rounds within 18 hours. What is the distance between A and B? | + | A truck moved from A to B at a speed of <math>50</math> km/h and returns from B to A at <math>70</math> km/h. It traveled <math>3</math> rounds within 18 hours. What is the distance between A and B? |
[[1997 PMWC Problems/Problem I13|Solution]] | [[1997 PMWC Problems/Problem I13|Solution]] | ||
== Problem I14 == | == Problem I14 == | ||
| − | If we make five two-digit numbers using the digits 0, 1, 2,...9 exactly once, and the product of the five numbers is maximized, find the greatest number among them. | + | If we make five two-digit numbers using the digits <math>0, 1, 2,...9</math> exactly once, and the product of the five numbers is maximized, find the greatest number among them. |
[[1997 PMWC Problems/Problem I14|Solution]] | [[1997 PMWC Problems/Problem I14|Solution]] | ||
| Line 104: | Line 104: | ||
Evaluate | Evaluate | ||
| − | < | + | <cmath>\begin{eqnarray*} |
| − | + | && 1 \left(\dfrac{1}{1}+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+\dfrac{1}{8}+\dfrac{1}{9}+\dfrac{1}{10}\right) \ | |
| − | + | &+& 3\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+\dfrac{1}{8}+\dfrac{1}{9}+\dfrac{1}{10}\right)\ | |
| − | + | &+&5\left(\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+\dfrac{1}{8}+\dfrac{1}{9}+\dfrac{1}{10}\right)\ | |
| − | + | &+&7\left(\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+\dfrac{1}{8}+\dfrac{1}{9}+\dfrac{1}{10}\right)\ | |
| − | + | &+&9\left(\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+\dfrac{1}{8}+\dfrac{1}{9}+\dfrac{1}{10}\right)+11\left(\dfrac{1}{6}+\dfrac{1}{7}+\dfrac{1}{8}+\dfrac{1}{9}+\dfrac{1}{10}\right)\ | |
| − | + | &+&13\left(\dfrac{1}{7}+\dfrac{1}{8}+\dfrac{1}{9}+\dfrac{1}{10}\right)+15\left(\dfrac{1}{8}+\dfrac{1}{9}+\dfrac{1}{10}\right)\ | |
| − | + | &+&17\left(\dfrac{1}{9}+\dfrac{1}{10}\right)+19\left(\dfrac{1}{10}\right)</cmath> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
[[1997 PMWC Problems/Problem T2|Solution]] | [[1997 PMWC Problems/Problem T2|Solution]] | ||
== Problem T3 == | == Problem T3 == | ||
| − | To type all the integers from 1 to 1997 using a typewriter on a piece of paper, how many | + | To type all the integers from <tt>1</tt> to <tt>1997</tt> using a typewriter on a piece of paper, how many does the key '<tt>9</tt>' needed to be pressed? |
| − | |||
[[1997 PMWC Problems/Problem T3|Solution]] | [[1997 PMWC Problems/Problem T3|Solution]] | ||
Revision as of 22:30, 9 January 2008
Contents
[hide]- 1 Problem I1
- 2 Problem I2
- 3 Problem I3
- 4 Problem I4
- 5 Problem I5
- 6 Problem I6
- 7 Problem I7
- 8 Problem I8
- 9 Problem I9
- 10 Problem I10
- 11 Problem I11
- 12 Problem I12
- 13 Problem I13
- 14 Problem I14
- 15 Problem I15
- 16 Problem T1
- 17 Problem T2
- 18 Problem T3
- 19 Problem T4
- 20 Problem T5
- 21 Problem T6
- 22 Problem T7
- 23 Problem T8
- 24 Problem T9
- 25 Problem T10
Problem I1
Evaluate ![]()
Problem I2
Problem I3
Peter is ill. He has to take medicine A every 8 hours, medicine B every 5 hours and medicine C every 10 hours. If he took all three medicines at 7 a.m. on Tuesday, when will he take them altogether again?
Problem I4
Problem I5
Problem I6
John and Mary went to a book shop and bought some exercise books. They had <dollar/>100 each. John could buy 7 large and 4 small ones. Mary could buy 5 large and 6 small ones and had <dollar/>5 left. How much was a small exercise book?
Problem I7
40% of girls and 50% of boys in a class got an 'A'. If there are only 12 students in the class who got 'A's and the ratio of boys and girls in the class is 45, how many students are there in the class?
Problem I8
![]()
Problem I9
A chemist mixed an acid of 48% concentration with the same acid of 80% concentration, and then added 2 litres of distilled water to the mixed acid. As a result, he got 10 litres of the acid of 40% concentration. How many millilitre of the acid of 48% concentration that the chemist had used? (1 litre = 1000 millilitres)
Problem I10
Mary took 24 chickens to the market. In the morning she
sold the chickens at ![]() 7 each and she only sold out less than
half of them. In the afternoon she discounted the price of
each chicken but the price was still an integral number in
dollar. In the afternoon she could sell all the chickens, and
she got totally
7 each and she only sold out less than
half of them. In the afternoon she discounted the price of
each chicken but the price was still an integral number in
dollar. In the afternoon she could sell all the chickens, and
she got totally ![]() 132 for the whole day. How many
chickens were sold in the morning?
132 for the whole day. How many
chickens were sold in the morning?
Problem I11
A rectangle ![]() is made up of five small congruent rectangles as shown in the given figure. Find the perimeter, in cm, of
is made up of five small congruent rectangles as shown in the given figure. Find the perimeter, in cm, of ![]() if its area is
if its area is ![]() .
.
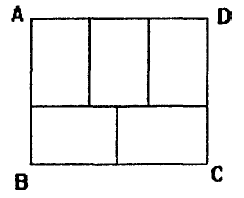
Problem I12
In a die, 1 and 6,2 and 5,3 and 4 appear on opposite faces. When 2 dice are thrown, product of numbers appearing on the top and bottom faces of the 2 dice are formed as follows:
number on top face of 1st die x number on top face of 2nd die number on top face of 1st die x number on bottom face of 2nd die number on bottom face of 1st die x number on top face of 2nd die number on bottom face of 1st die x number on bottom face of 2nd die
What is the sum of these 4 products ?
Problem I13
A truck moved from A to B at a speed of ![]() km/h and returns from B to A at
km/h and returns from B to A at ![]() km/h. It traveled
km/h. It traveled ![]() rounds within 18 hours. What is the distance between A and B?
rounds within 18 hours. What is the distance between A and B?
Problem I14
If we make five two-digit numbers using the digits ![]() exactly once, and the product of the five numbers is maximized, find the greatest number among them.
exactly once, and the product of the five numbers is maximized, find the greatest number among them.
Problem I15
How many paths from A to B consist of exactly six line
segments (vertical, horizontal or inclined)?
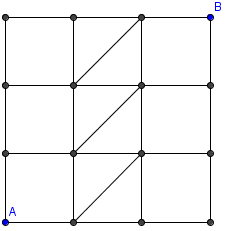
Problem T1
Problem T2
Evaluate
\begin{eqnarray*}
&& 1 \left(\dfrac{1}{1}+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+\dfrac{1}{8}+\dfrac{1}{9}+\dfrac{1}{10}\right) \\
&+& 3\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+\dfrac{1}{8}+\dfrac{1}{9}+\dfrac{1}{10}\right)\\
&+&5\left(\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+\dfrac{1}{8}+\dfrac{1}{9}+\dfrac{1}{10}\right)\\
&+&7\left(\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+\dfrac{1}{8}+\dfrac{1}{9}+\dfrac{1}{10}\right)\\
&+&9\left(\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+\dfrac{1}{8}+\dfrac{1}{9}+\dfrac{1}{10}\right)+11\left(\dfrac{1}{6}+\dfrac{1}{7}+\dfrac{1}{8}+\dfrac{1}{9}+\dfrac{1}{10}\right)\\
&+&13\left(\dfrac{1}{7}+\dfrac{1}{8}+\dfrac{1}{9}+\dfrac{1}{10}\right)+15\left(\dfrac{1}{8}+\dfrac{1}{9}+\dfrac{1}{10}\right)\\
&+&17\left(\dfrac{1}{9}+\dfrac{1}{10}\right)+19\left(\dfrac{1}{10}\right) (Error compiling LaTeX. Unknown error_msg)
Problem T3
To type all the integers from 1 to 1997 using a typewriter on a piece of paper, how many does the key '9' needed to be pressed?









