Difference between revisions of "2016 AIME II Problems/Problem 14"

Latest revision as of 18:39, 25 November 2024

Problem

Equilateral $\triangle ABC$ has side length $600$ . Points $P$ and $Q$ lie outside the plane of $\triangle ABC$ and are on opposite sides of the plane. Furthermore, $PA=PB=PC$ , and $QA=QB=QC$ , and the planes of $\triangle PAB$ and $\triangle QAB$ form a $120^{\circ}$ dihedral angle (the angle between the two planes). There is a point $O$ whose distance from each of $A,B,C,P,$ and $Q$ is $d$ . Find $d$ .

Solution 1

The inradius of $\triangle ABC$ is $100\sqrt 3$ and the circumradius is $200 \sqrt 3$ . Now, consider the line perpendicular to plane $ABC$ through the circumcenter of $\triangle ABC$ . Note that $P,Q,O$ must lie on that line to be equidistant from each of the triangle's vertices. Also, note that since $P, Q, O$ are collinear, and $OP=OQ$ , we must have $O$ is the midpoint of $PQ$ . Now, Let $K$ be the circumcenter of $\triangle ABC$ , and $L$ be the foot of the altitude from $A$ to $BC$ . We must have $\tan(\angle KLP+ \angle QLK)= \tan(120^{\circ})$ . Setting $KP=x$ and $KQ=y$ , assuming WLOG $x>y$ , we must have $\tan(120^{\circ})=-\sqrt{3}=\dfrac{\dfrac{x+y}{100 \sqrt{3}}}{\dfrac{30000-xy}{30000}}$ . Therefore, we must have $100(x+y)=xy-30000$ . Also, we must have $\left(\dfrac{x+y}{2}\right)^{2}=\left(\dfrac{x-y}{2}\right)^{2}+120000$ by the Pythagorean theorem, so we have $xy=120000$ , so substituting into the other equation we have $90000=100(x+y)$ , or $x+y=900$ . Since we want $\dfrac{x+y}{2}$ , the desired answer is $\boxed{450}$ .

Solution 2 (Short & Simple)

Draw a good diagram. Draw $CH$ as an altitude of the triangle. Scale everything down by a factor of $100\sqrt{3}$ , so that $AB=2\sqrt{3}$ . Finally, call the center of the triangle U. Draw a cross-section of the triangle via line $CH$ , which of course includes $P, Q$ . From there, we can call $OU=h$ . There are two crucial equations we can thus generate. WLOG set $PU<QU$ , then we call $PU=d-h, QU=d+h$ . First equation: using the Pythagorean Theorem on $\triangle UOB$ , $h^2+2^2=d^2$ . Next, using the tangent addition formula on angles $\angle PHU, \angle UHQ$ we see that after simplifying $-d^2+h^2=-4, 2d=3\sqrt{3}$ in the numerator, so $d=\frac{3\sqrt{3}}{2}$ . Multiply back the scalar and you get $\boxed{450}$ . Not that hard, was it?

Solution 3

To make numbers more feasible, we'll scale everything down by a factor of $100$ so that $\overline{AB}=\overline{BC}=\overline{AC}=6$ . We should also note that $P$ and $Q$ must lie on the line that is perpendicular to the plane of $ABC$ and also passes through the circumcenter of $ABC$ (due to $P$ and $Q$ being equidistant from $A$ , $B$ , $C$ ), let $D$ be the altitude from $C$ to $AB$ . We can draw a vertical cross-section of the figure then: $[asy]pair C, D, I, P, Q, O; D=(0,0); C=(5.196152,0); P=(1.732051,7.37228); I=(1.732051,0); Q=(1.732051,-1.62772); O=(1.732051,2.87228); draw(C--Q--D--P--cycle); draw(C--D, dashed); draw(P--Q, dotted); draw(O--C, dotted); label("$C$", C, E); label("$D$", D, W); label("$I$", I, NW); label("$P$", P, N); label("$Q$", Q, S); label("$O$", O, SW); dot(O); dot(I);[/asy]$ We let $\angle PDI=\alpha$ so $\angle QDI=120^{\circ}-\alpha$ , also note that $\overline{PO}=\overline{QO}=\overline{CO}=d$ . Because $I$ is the centroid of $ABC$ , we know that ratio of $\overline{CI}$ to $\overline{DI}$ is $2:1$ . Since we've scaled the figure down, the length of $CD$ is $3\sqrt{3}$ , from this it's easy to know that $\overline{CI}=2\sqrt{3}$ and $\overline{DI}=\sqrt{3}$ . The following two equations arise: $\begin{align} \sqrt{3}\tan{\left(\alpha\right)}+\sqrt{3}\tan{\left(120^{\circ}-\alpha\right)}&=2d \\ \sqrt{3}\tan{\left(\alpha\right)} - d &= \sqrt{d^{2}-12} \end{align}$ Using trig identities for the tangent, we find that $\begin{align*} \sqrt{3}\tan{\left(120^{\circ}-\alpha\right)}&=\sqrt{3}\left(\frac{\tan{\left(120^{\circ}\right)}+\tan{\left(\text{-}\alpha\right)}}{1-\tan{\left(120^{\circ}\right)}\tan{\left(\text{-}\alpha\right)}}\right) \\ &= \sqrt{3}\left(\frac{\text{-}\sqrt{3}+\tan{\left(\text{-}\alpha\right)}}{1+\sqrt{3}\tan{\left(\text{-}\alpha\right)}}\right) \\ &= \sqrt{3}\left(\frac{\text{-}\sqrt{3}-\tan{\left(\alpha\right)}}{1-\sqrt{3}\tan{\left(\alpha\right)}}\right) \\ &= \frac{\sqrt{3}\tan{\left(\alpha\right)}+3}{\sqrt{3}\tan{\left(\alpha\right)}-1}.\end{align*}$ Okay, now we can plug this into $\left(1\right)$ to get: $\begin{align}\sqrt{3}\tan{\left(\alpha\right)}+\frac{\sqrt{3}\tan{\left(\alpha\right)}+3}{\sqrt{3}\tan{\left(\alpha\right)}-1}&=2d \\ \sqrt{3}\tan{\left(\alpha\right)} - d &= \sqrt{d^{2}-12} \end{align}$ Notice that $\alpha$ only appears in the above system of equations in the form of $\sqrt{3}\tan{\left(\alpha\right)}$ , we can set $\sqrt{3}\tan{\left(\alpha\right)}=a$ for convenience since we really only care about $d$ . Now we have $\begin{align}a+\frac{a+3}{a-1}&=2d \\ a - d &= \sqrt{d^{2}-12} \end{align}$ Looking at $\left(2\right)$ , it's tempting to square it to get rid of the square-root so now we have: $\begin{align*}a^{2}-2ad+d^{2}&=d^{2}-12 \\ a - 2ad &= \text{-}12 \end{align*}$ See the sneaky $2d$ in the above equation? That we means we can substitute it for $a+\frac{a+3}{a-1}$ : $\begin{align*}a^{2}-2ad+d^{2}&=d^{2}-12 \\ a^{2} - a\left(a+\frac{a+3}{a-1}\right) &= \text{-}12 \\ a^{2}-a^{2}-\frac{a^{2}+3a}{a-1} &=\text{-}12 \\ -\frac{a^{2}+3a}{a-1}&=\text{-}12 \\ \text{-}a^{2}-3a&=\text{-}12a+12 \\ 0 &= a^{2}-9a+12 \end{align*}$ Use the quadratic formula, we find that $a=\frac{9\pm\sqrt{9^{2}-4\left(1\right)\left(12\right)}}{2\left(1\right)}=\frac{9\pm\sqrt{33}}{2}$ - the two solutions were expected because $a$ can be $\angle PDI$ or $\angle QDI$ . We can plug this into $\left(1\right)$ : $\begin{align*}a+\frac{a+3}{a-1}&=2d \\ \frac{9\pm\sqrt{33}}{2}+\frac{\frac{9\pm\sqrt{33}}{2}+3}{\frac{9\pm\sqrt{33}}{2}-1}=2d \\ \frac{9\pm\sqrt{33}}{2}+\frac{15\pm\sqrt{33}}{7\pm\sqrt{33}} &= 2d\end{align*}$ I'll use $a=\frac{9+\sqrt{33}}{2}$ because both values should give the same answer for $d$ . $\begin{align*} \frac{9+\sqrt{33}}{2}+\frac{15+\sqrt{33}}{7+\sqrt{33}} &= 2d \\ \frac{\left(9+\sqrt{33}\right)\left(7+\sqrt{33}\right)+\left(2\right)\left(15+\sqrt{33}\right)}{\left(2\right)\left(7+\sqrt{33}\right)} &= 2d \\ \frac{63+33+16\sqrt{33}+30+2\sqrt{33}}{14+2\sqrt{33}} &= 2d \\ \frac{126+18\sqrt{33}}{14+2\sqrt{33}} &= 2d \\ 9 &= 2d \\ \frac{9}{2} &= d\end{align*}$ Wait! Before you get excited, remember that we scaled the entire figure by $100$ ?? That means that the answer is $d=100\times\frac{9}{2}=\boxed{450}$ . -fatant

Solution 4

We use the diagram from solution 3. From basic angle chasing, $180=\angle{QOC}+\angle{CO}P=2\angle{OCP}+2\angle{OCQ}=2\angle{QCP}$ so triangle QCP is a right triangle. This means that triangles $CQI$ and $CPI$ are similar. If we let $\angle{IDQ}=x$ and $\angle{PDI}=y$ , then we know $x+y=120$ and $\frac{PG}{GC}=\frac{GC}{GQ}\Rightarrow\frac{100\sqrt{3}\tan{y}}{200\sqrt{3}}=\frac{200\sqrt{3}}{100\sqrt{3}\tan{x}}\Rightarrow\tan{x}\tan{y}=4$ We also know that $PQ=2d=100\sqrt{3}(\tan{x}+\tan{y})$ $d=50\sqrt{3}(\tan{x}+\tan{y})$ $\frac{d}{1-\tan{x}\tan{y}}=50\sqrt{3}\cdot\frac{\tan{x}+\tan{y}}{1-\tan{x}\tan{y}}$ $\frac{d}{-3}=50\sqrt{3}\tan{(x+y)}$ $d=-150\sqrt{3}\tan{120}=-150\sqrt{3}(-\sqrt{3})=\boxed{450}$

-EZmath2006

Solution 5

We use the diagram from solution 3.

Let $BP = a$ and $BQ = b$ . Then, by Stewart's on $BPQ$ , we find $2x^3 + 2x^3 = a^2x + b^2x \implies a^2 + b^2 = 4x^2.$

The altitude from $P$ to $ABC$ is $\sqrt{a^2 - (200\sqrt{3})^2}$ so $PQ = 2x = \sqrt{a^2 - (200\sqrt{3})^2} + \sqrt{b^2 - (200\sqrt{3})^2}.$

Furthermore, the altitude from $P$ to $AB$ is $\sqrt{a^2 - 300^2}$ , so, by LoC and the dihedral condition, $a^2 - 300^2 + b^2 - 300^2 + \sqrt{a^2 - 300^2}\sqrt{b^2-300^2} = 4x^2.$

Squaring the equation for $PQ$ and substituting $a^2 + b^2 = 4x^2$ yields $2\sqrt{a^2 - (200\sqrt{3})^2}\sqrt{b^2 - (200\sqrt{3})^2} = 6\cdot 200^2.$

Substituting $a^2 + b^2 = 4x^2$ into the other equation, $\sqrt{a^2 - 300^2}\sqrt{b^2-300^2} = 2\cdot 300^2.$

Squaring both of these gives $a^2b^2-3\cdot 200^2(a^2 + b^2) + 9\cdot 200^4 = 9\cdot 200^4$ $a^2b^2 - 300^2(a^2+b^2) + 300^4 = 4\cdot 300^4.$

Substituting $a^2 + b^2 = 4x^2$ and solving for $x$ gives $\boxed{450}$ , as desired.

-mathtiger6

Solution 6 (Geometry)

Let $AB = a, M$ be midpoint $BC, I$ be the center of equilateral $\triangle ABC,$ $IM = b = \frac {a}{2\sqrt{3}}, O$ be the center of sphere $ABCPQ.$ Then $AI = 2b, AO = BO = PO =QO = d.$ $QA=QB=QC,PA=PB=PC \implies$ $POIQ\perp ABC, \angle PMQ = 120^\circ.$ (See upper diagram).

We construct the circle PQMD, use the formulas for intersecting chords and get $DI = 5b, FI = EO = \frac{3b}{2}$ $\implies FM = \frac{5b}{2}.$ (See lower diagram).

We apply the Law of Sine to $\triangle PMQ$ and get $2EM \sin 120^\circ =PQ$ $\implies r \sqrt{3} = 2d$ $\implies 3r^2 = 4d^2.$ We apply the Pythagorean Law on $\triangle AOI$ and $\triangle EFM$ and get $d^2 = 4b^2 + OI^2, r^2 = \frac {25b^2}{4} + EF^2 \implies$ $r = 3b\implies d = \frac {3a}{2} = \boxed {450}.$ vladimir.shelomovskii@gmail.com, vvsss

Solution 7

Let $M$ be the midpoint of $\overline{AB}$ and $X$ the center of $\triangle ABC$ . Then $P, O, Q, M, X, C$ all lie in the same vertical plane. We can make the following observations:

The equilateral triangle has side length $600$ , so $MC=300\sqrt{3}$ and $X$ divides $MC$ so that $MX=100\sqrt{3}$ and $XC=200\sqrt{3}$ ;
$O$ is the midpoint of $PQ$ since $O$ is equidistant from $A, B, C, P, Q$ – it is also the circumcenter of $\triangle PCQ$ ;
$\angle PMQ=120^{\circ}$ , the dihedral angle.

To make calculations easier, we will denote $100\sqrt{3}=m$ , so that $MX=m$ and $XC=2m$ .

$[asy] unitsize(20); pair P = (0, 12); pair Q = (0, -3); pair O = (P+Q)/2; pair M = (-3, 0); pair X = (0, 0); pair C = (6, 0); draw(P--O--Q); draw(M--X--C); draw(P--M--Q, blue); draw(Q--C--P); draw(circle((0, 4.5), 7.5)); label("$P$", P, N); label("$Q$", Q, S); label("$O$", O, E); dot(O); label("$M$", M, W); label("$X$", X, NE); label("$C$", C, E); label("$m$", (M+X)/2, N); label("$2m$", (X+C)/2, N); [/asy]$

Denote $PX=p$ and $QX=q$ , where the tangent addition formula on $\triangle PMQ$ yields $\frac{\tan\measuredangle PMX+\tan\measuredangle QMX}{1-\tan\measuredangle PMX\tan\measuredangle QMX}=\tan(120^{\circ})=-\sqrt{3}.$ Using $\tan\measuredangle PMX=\frac{p}{m}$ and $\tan\measuredangle QMX=\frac{q}{m}$ , we have $\frac{\frac{p}{m}+\frac{q}{m}}{1-\frac{p}{m}\cdot\frac{q}{m}}=-\sqrt{3}.$ After multiplying both numerator and denominator by $m^{2}$ we have $\frac{(p+q)m}{m^{2}-pq}=-\sqrt{3}.$ But note that $pq=(2m)(2m)=4m^{2}$ by power of a point at $X$ , where we deduce by symmetry that $MM^{\prime}=MX=m$ on the diagram below: $[asy] unitsize(20); pair P = (0, 12); pair Q = (0, -3); pair O = (P+Q)/2; pair M = (-3, 0); pair Mprime = (-6, 0); pair X = (0, 0); pair C = (6, 0); draw(P--O--Q); draw(Mprime--M--X--C); draw(P--M--Q, blue); draw(Q--C--P); draw(circle((0, 4.5), 7.5)); label("$P$", P, N); label("$Q$", Q, S); label("$O$", O, E); dot(O); label("$M$", M, S); label("$M^{\prime}$", Mprime, W); label("$X$", X, SE); label("$C$", C, E); label("$m$", (Mprime+M)/2, N); label("$m$", (M+X)/2, N); label("$2m$", (X+C)/2, N); [/asy]$

Thus $\begin{align*} \frac{(p+q)m}{m^{2}-4m^{2}}=-\sqrt{3} \\ \frac{p+q}{-3m}=-\sqrt{3} \\ p+q=\left(-\sqrt{3}\right)\left(-3m\right) \\ p+q=3\sqrt{3}\cdot m.\end{align*}$ Earlier we assigned the variable $m$ to the length $100\sqrt{3}$ which implies $PQ=\left(3\sqrt{3}\right)\left(100\sqrt{3}\right)=900$ . Thus the distance $d$ is equal to $\frac{PQ}{2}=\boxed{450}$ .

Solution 8 (Law of Cosines)

Let $Z$ be the center of $\triangle ABC$ . Let $A’$ be the midpoint of $BC$ . Let $ZA’ = c = 100\sqrt{3}$ and $ZA = 2c = 200\sqrt{3}$ . Let $PZ = a$ and $QZ = b$ . We will be working in the plane that contains the points: $A$ , $P$ , $A’$ , $Q$ , $O$ , and $Z$ .

Since $P$ , $O$ , and $Q$ are collinear and $PO = QO = AO$ , $\triangle PAQ$ is a right triangle with $\angle PAQ = 90^{\circ}$ . Since $AZ \perp PQ$ , $(PZ)(QZ) = (AZ)^2 = ab = (2c)^2 = 120000$ .

$PA’ = \sqrt{a^2 + c^2}$ , $QA’ = \sqrt{b^2 + c^2}$ , $PQ = a + b$ , and $\angle PAQ = 120^{\circ}$ . By Law of Cosines $(a + b)^2 = a^2 + b^2 + 2c^2 + \sqrt{a^2b^2 + a^2c^2 + b^2c^2 + c^4}$ . Substituting $4c^2$ for $ab$ and simplifying, we get $6c = \sqrt{17c^2 + a^2 + b^2}$ . Squaring and simplifying, we get $a^2 + b^2 = 19c^2 = 570000$ . Adding $2ab = 8c^2$ to both sides we get $PQ = a + b = 900$ . Since $O$ is the midpoint of $PQ$ , $d = PO = \boxed{450}$

~numerophile

Solution 9 (Coordinate Bash)

Set $AB = s, M$ as midpoint $BC, I$ as the center of equilateral $\triangle ABC,$ and by $30-60-90$ triangle formulas, we know $IM = b = \frac {s}{2\sqrt{3}}, IA = IB = IC = \frac{s}{\sqrt{3}}$ .

First note that $P$ and $Q$ are on the line perpendicular to plane $ABC$ through the circumcenter of $\triangle ABC$ . Then notice that point $O$ is the midpoint of $PQ$ , so it also lies on this axis. Then, we see that the position of $O$ relative to the triangle fully determines the positions of both $P$ and $Q$ , so setting the coordinates of $O$ as $(0,0,h)$ where the origin is defined the circumcenter and $\triangle ABC$ lies in the $xy$ -plane, we get: $\begin{align*} OA^2 = OB^2 = OC^2 = h^2+\frac{s^2}{3} = OP^2 = OQ^2 \end{align*}$

Thus, the coordinates of $P$ and $Q$ are $(0,0,h\pm\sqrt{h^2+\frac{s^2}{3}})$ . Now we make use of the angle condition. WLOG set the coordinates of $M$ as $(\frac{s}{2\sqrt{3}},0,0)$ . We know the angle between $PM$ and $QM$ is $120^{\circ}$ , so after solving for the vectors, taking their dot product, equating it to $PM \cdot QM \cdot\cos{120^{\circ}}$ , and $\textit{finally}$ solving for $h$ in terms of $s$ , we get $h^2 = \frac{11}{48}s^2 \\ \implies OA^2 = h^2 + \frac{s^2}{3} = \frac{27}{48}s^2 \\ \implies OA = \frac{3}{4}s = \boxed{450}$

(If someone feels like it, please feel free to fill in the rest of the details!)

~ninjaforce

Video Solution by MOP 2024

https://youtu.be/hyhIlsAR2hs

~r00tsOfUnity

@@ Line 1: / Line 1: @@
+==Problem==
 Equilateral <math>\triangle ABC</math> has side length <math>600</math>. Points <math>P</math> and <math>Q</math> lie outside the plane of <math>\triangle ABC</math> and are on opposite sides of the plane. Furthermore, <math>PA=PB=PC</math>, and <math>QA=QB=QC</math>, and the planes of <math>\triangle PAB</math> and <math>\triangle QAB</math> form a <math>120^{\circ}</math> dihedral angle (the angle between the two planes). There is a point <math>O</math> whose distance from each of <math>A,B,C,P,</math> and <math>Q</math> is <math>d</math>. Find <math>d</math>.
-==Solution==
+==Solution 1==
-The inradius of <math>\triangle ABC</math> is <math>100\sqrt 3</math> and the circumradius is <math>200 \sqrt 3</math>. Now, consider the line perpendicular to plane <math>ABC</math> through the circumcenter of <math>\triangle ABC</math>. Note that <math>P,Q,O</math> must lie on that line to be equidistant from each of the triangle's vertices. Also, note that since <math>P, Q, O</math> are collinear, and <math>OP=OQ</math>, we must have <math>O</math> is the midpoint of <math>PQ</math>.  Now, Let <math>K</math> be the circumcenter of <math>\triangle ABC</math>, and <math>L</math> be the foot of the altitude from <math>A</math> to <math>BC</math>. We must have <math>\tan(\angle KLP+ \angle QLK)= \tan(120^{\circ})</math>. Setting <math>KP=x</math> and <math>KQ=y</math>, assuming WLOG <math>x>y</math>, we must have <math>(\tan(120^{\circ})=-\sqrt{3}=\dfrac{\dfrac{x+y}{100\sqrt{3}}}{\dfrac{30000-xy}{30000}</math>. Therefore, we must have <math>100(x+y)=xy-30000</math>. Also, we must have <math>(\dfrac{x+y}{2})^{2}=(\dfrac{x-y}{2})^{2}+120000</math> by the Pythagorean theorem, so we have <math>xy=120000</math>, so substituting into the other equation we have <math>90000=100(x+y)</math>, or <math>x+y=900</math>. Since we want <math>\dfrac{x+y}{2}</math>, the desired answer is <math>\boxed{450}</math>.
+The inradius of <math>\triangle ABC</math> is <math>100\sqrt 3</math> and the circumradius is <math>200 \sqrt 3</math>. Now, consider the line perpendicular to plane <math>ABC</math> through the circumcenter of <math>\triangle ABC</math>. Note that <math>P,Q,O</math> must lie on that line to be equidistant from each of the triangle's vertices. Also, note that since <math>P, Q, O</math> are collinear, and <math>OP=OQ</math>, we must have <math>O</math> is the midpoint of <math>PQ</math>.  Now, Let <math>K</math> be the circumcenter of <math>\triangle ABC</math>, and <math>L</math> be the foot of the altitude from <math>A</math> to <math>BC</math>. We must have <math>\tan(\angle KLP+ \angle QLK)= \tan(120^{\circ})</math>. Setting <math>KP=x</math> and <math>KQ=y</math>, assuming WLOG <math>x>y</math>, we must have <math>\tan(120^{\circ})=-\sqrt{3}=\dfrac{\dfrac{x+y}{100 \sqrt{3}}}{\dfrac{30000-xy}{30000}}</math>. Therefore, we must have <math>100(x+y)=xy-30000</math>. Also, we must have <math>\left(\dfrac{x+y}{2}\right)^{2}=\left(\dfrac{x-y}{2}\right)^{2}+120000</math> by the Pythagorean theorem, so we have <math>xy=120000</math>, so substituting into the other equation we have <math>90000=100(x+y)</math>, or <math>x+y=900</math>. Since we want <math>\dfrac{x+y}{2}</math>, the desired answer is <math>\boxed{450}</math>.
+==Solution 2 (Short & Simple)==
+Draw a good diagram. Draw <math>CH</math> as an altitude of the triangle. Scale everything down by a factor of <math>100\sqrt{3}</math>, so that <math>AB=2\sqrt{3}</math>. Finally, call the center of the triangle U. Draw a cross-section of the triangle via line <math>CH</math>, which of course includes <math>P, Q</math>. From there, we can call <math>OU=h</math>. There are two crucial equations we can thus generate. WLOG set <math>PU<QU</math>, then we call <math>PU=d-h, QU=d+h</math>. First equation: using the Pythagorean Theorem on <math>\triangle UOB</math>, <math>h^2+2^2=d^2</math>. Next, using the tangent addition formula on angles <math>\angle PHU, \angle UHQ</math> we see that after simplifying <math>-d^2+h^2=-4, 2d=3\sqrt{3}</math> in the numerator, so <math>d=\frac{3\sqrt{3}}{2}</math>. Multiply back the scalar and you get <math>\boxed{450}</math>. Not that hard, was it?
+==Solution 3==
+To make numbers more feasible, we'll scale everything down by a factor of <math>100</math> so that <math>\overline{AB}=\overline{BC}=\overline{AC}=6</math>. We should also note that <math>P</math> and <math>Q</math> must lie on the line that is perpendicular to the plane of <math>ABC</math> and also passes through the circumcenter of <math>ABC</math> (due to <math>P</math> and <math>Q</math> being equidistant from <math>A</math>, <math>B</math>, <math>C</math>), let <math>D</math> be the altitude from <math>C</math> to <math>AB</math>. We can draw a vertical cross-section of the figure then: <asy>pair C, D, I, P, Q, O; D=(0,0); C=(5.196152,0); P=(1.732051,7.37228); I=(1.732051,0); Q=(1.732051,-1.62772); O=(1.732051,2.87228); draw(C--Q--D--P--cycle); draw(C--D, dashed); draw(P--Q, dotted); draw(O--C, dotted); label("$C$", C, E); label("$D$", D, W); label("$I$", I, NW); label("$P$", P, N);  label("$Q$", Q, S);  label("$O$", O, SW); dot(O); dot(I);</asy> We let <math>\angle PDI=\alpha</math> so <math>\angle QDI=120^{\circ}-\alpha</math>, also note that <math>\overline{PO}=\overline{QO}=\overline{CO}=d</math>. Because <math>I</math> is the centroid of <math>ABC</math>, we know that ratio of <math>\overline{CI}</math> to <math>\overline{DI}</math> is <math>2:1</math>. Since we've scaled the figure down, the length of <math>CD</math> is <math>3\sqrt{3}</math>, from this it's easy to know that <math>\overline{CI}=2\sqrt{3}</math> and <math>\overline{DI}=\sqrt{3}</math>. The following two equations arise: <cmath>\begin{align} \sqrt{3}\tan{\left(\alpha\right)}+\sqrt{3}\tan{\left(120^{\circ}-\alpha\right)}&=2d \\ \sqrt{3}\tan{\left(\alpha\right)} - d &= \sqrt{d^{2}-12} \end{align}</cmath> Using trig identities for the tangent, we find that <cmath>\begin{align*} \sqrt{3}\tan{\left(120^{\circ}-\alpha\right)}&=\sqrt{3}\left(\frac{\tan{\left(120^{\circ}\right)}+\tan{\left(\text{-}\alpha\right)}}{1-\tan{\left(120^{\circ}\right)}\tan{\left(\text{-}\alpha\right)}}\right) \\ &= \sqrt{3}\left(\frac{\text{-}\sqrt{3}+\tan{\left(\text{-}\alpha\right)}}{1+\sqrt{3}\tan{\left(\text{-}\alpha\right)}}\right) \\ &= \sqrt{3}\left(\frac{\text{-}\sqrt{3}-\tan{\left(\alpha\right)}}{1-\sqrt{3}\tan{\left(\alpha\right)}}\right) \\ &= \frac{\sqrt{3}\tan{\left(\alpha\right)}+3}{\sqrt{3}\tan{\left(\alpha\right)}-1}.\end{align*}</cmath> Okay, now we can plug this into <math>\left(1\right)</math> to get: <cmath>\begin{align}\sqrt{3}\tan{\left(\alpha\right)}+\frac{\sqrt{3}\tan{\left(\alpha\right)}+3}{\sqrt{3}\tan{\left(\alpha\right)}-1}&=2d \\ \sqrt{3}\tan{\left(\alpha\right)} - d &= \sqrt{d^{2}-12} \end{align}</cmath> Notice that <math>\alpha</math> only appears in the above system of equations in the form of <math>\sqrt{3}\tan{\left(\alpha\right)}</math>, we can set <math>\sqrt{3}\tan{\left(\alpha\right)}=a</math> for convenience since we really only care about <math>d</math>. Now we have <cmath>\begin{align}a+\frac{a+3}{a-1}&=2d \\ a - d &= \sqrt{d^{2}-12} \end{align}</cmath> Looking at <math>\left(2\right)</math>, it's tempting to square it to get rid of the square-root so now we have: <cmath>\begin{align*}a^{2}-2ad+d^{2}&=d^{2}-12 \\ a - 2ad &= \text{-}12 \end{align*}</cmath> See the sneaky <math>2d</math> in the above equation? That we means we can substitute it for <math>a+\frac{a+3}{a-1}</math>: <cmath>\begin{align*}a^{2}-2ad+d^{2}&=d^{2}-12 \\ a^{2} - a\left(a+\frac{a+3}{a-1}\right) &= \text{-}12 \\ a^{2}-a^{2}-\frac{a^{2}+3a}{a-1} &=\text{-}12 \\ -\frac{a^{2}+3a}{a-1}&=\text{-}12 \\ \text{-}a^{2}-3a&=\text{-}12a+12 \\ 0 &= a^{2}-9a+12 \end{align*}</cmath> Use the quadratic formula, we find that <math>a=\frac{9\pm\sqrt{9^{2}-4\left(1\right)\left(12\right)}}{2\left(1\right)}=\frac{9\pm\sqrt{33}}{2}</math> - the two solutions were expected because <math>a</math> can be <math>\angle PDI</math> or <math>\angle QDI</math>. We can plug this into <math>\left(1\right)</math>: <cmath>\begin{align*}a+\frac{a+3}{a-1}&=2d \\ \frac{9\pm\sqrt{33}}{2}+\frac{\frac{9\pm\sqrt{33}}{2}+3}{\frac{9\pm\sqrt{33}}{2}-1}=2d \\ \frac{9\pm\sqrt{33}}{2}+\frac{15\pm\sqrt{33}}{7\pm\sqrt{33}} &= 2d\end{align*}</cmath> I'll use <math>a=\frac{9+\sqrt{33}}{2}</math> because both values should give the same answer for <math>d</math>. <cmath>\begin{align*} \frac{9+\sqrt{33}}{2}+\frac{15+\sqrt{33}}{7+\sqrt{33}} &= 2d \\ \frac{\left(9+\sqrt{33}\right)\left(7+\sqrt{33}\right)+\left(2\right)\left(15+\sqrt{33}\right)}{\left(2\right)\left(7+\sqrt{33}\right)} &= 2d \\ \frac{63+33+16\sqrt{33}+30+2\sqrt{33}}{14+2\sqrt{33}} &= 2d \\ \frac{126+18\sqrt{33}}{14+2\sqrt{33}} &= 2d \\ 9 &= 2d \\ \frac{9}{2} &= d\end{align*}</cmath> Wait! Before you get excited, remember that we scaled the entire figure by <math>100</math>?? That means that the answer is <math>d=100\times\frac{9}{2}=\boxed{450}</math>.
+-fatant
+==Solution 4==
+We use the diagram from solution 3. From basic angle chasing,
+<cmath>180=\angle{QOC}+\angle{CO}P=2\angle{OCP}+2\angle{OCQ}=2\angle{QCP}</cmath>
+so triangle QCP is a right triangle. This means that triangles <math>CQI</math> and <math>CPI</math> are similar. If we let <math>\angle{IDQ}=x</math> and <math>\angle{PDI}=y</math>, then we know <math>x+y=120</math> and <cmath>\frac{PG}{GC}=\frac{GC}{GQ}\Rightarrow\frac{100\sqrt{3}\tan{y}}{200\sqrt{3}}=\frac{200\sqrt{3}}{100\sqrt{3}\tan{x}}\Rightarrow\tan{x}\tan{y}=4</cmath> We also know that <cmath>PQ=2d=100\sqrt{3}(\tan{x}+\tan{y})</cmath> <cmath>d=50\sqrt{3}(\tan{x}+\tan{y})</cmath> <cmath>\frac{d}{1-\tan{x}\tan{y}}=50\sqrt{3}\cdot\frac{\tan{x}+\tan{y}}{1-\tan{x}\tan{y}}</cmath> <cmath>\frac{d}{-3}=50\sqrt{3}\tan{(x+y)}</cmath> <cmath>d=-150\sqrt{3}\tan{120}=-150\sqrt{3}(-\sqrt{3})=\boxed{450}</cmath>
+-EZmath2006
+==Solution 5==
+We use the diagram from solution 3.
+Let <math>BP = a</math> and <math>BQ = b</math>. Then, by Stewart's on <math>BPQ</math>, we find
+<cmath>2x^3 + 2x^3 = a^2x + b^2x \implies a^2 + b^2 = 4x^2.</cmath>
+The altitude from <math>P</math> to <math>ABC</math> is <math>\sqrt{a^2 - (200\sqrt{3})^2}</math> so
+<cmath>PQ = 2x = \sqrt{a^2 - (200\sqrt{3})^2} + \sqrt{b^2 - (200\sqrt{3})^2}.</cmath>
+Furthermore, the altitude from <math>P</math> to <math>AB</math> is <math>\sqrt{a^2 - 300^2}</math>, so, by LoC and the dihedral condition,
+<cmath>a^2 - 300^2 + b^2 - 300^2 + \sqrt{a^2 - 300^2}\sqrt{b^2-300^2} = 4x^2.</cmath>
+Squaring the equation for <math>PQ</math> and substituting <math>a^2 + b^2  = 4x^2</math> yields
+<cmath>2\sqrt{a^2 - (200\sqrt{3})^2}\sqrt{b^2 - (200\sqrt{3})^2} = 6\cdot 200^2.</cmath>
+Substituting <math>a^2 + b^2 = 4x^2</math> into the other equation,
+<cmath>\sqrt{a^2 - 300^2}\sqrt{b^2-300^2} = 2\cdot 300^2.</cmath>
+Squaring both of these gives
+<cmath>a^2b^2-3\cdot 200^2(a^2 + b^2) + 9\cdot 200^4 = 9\cdot 200^4</cmath>
+<cmath>a^2b^2 - 300^2(a^2+b^2) + 300^4 = 4\cdot 300^4.</cmath>
+Substituting <math>a^2 + b^2 = 4x^2</math> and solving for <math>x</math> gives <math>\boxed{450}</math>, as desired.
+-mathtiger6
+==Solution 6 (Geometry)==
+[[File:2016 AIME II 14.png|400px|right]]
+[[File:2016 AIME II 14a.png|400px|right]]
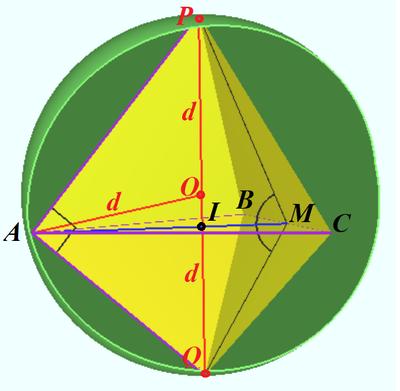
+Let <math>AB = a, M</math> be midpoint <math>BC, I</math> be the center of equilateral <math>\triangle ABC,</math>
+<math>IM = b = \frac {a}{2\sqrt{3}}, O</math> be the center of sphere <math>ABCPQ.</math>
+Then <cmath>AI = 2b, AO = BO = PO =QO = d.</cmath>
+<cmath>QA=QB=QC,PA=PB=PC \implies</cmath>
+<cmath>POIQ\perp ABC, \angle PMQ = 120^\circ.</cmath>
+(See upper diagram).
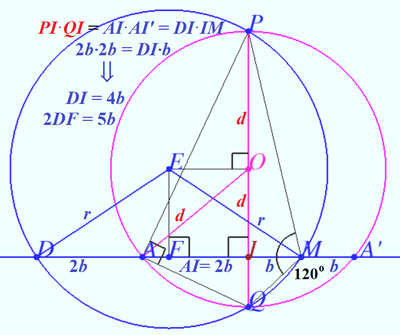
+We construct the circle PQMD, use the formulas for  intersecting chords and get
+<cmath>DI = 5b, FI = EO = \frac{3b}{2}</cmath>
+<cmath>\implies FM = \frac{5b}{2}.</cmath>
+(See lower diagram).
+We apply the Law of Sine to <math>\triangle PMQ</math> and get
+<cmath>2EM \sin 120^\circ =PQ</cmath>
+<cmath>\implies r \sqrt{3} = 2d</cmath>
+<cmath>\implies 3r^2 = 4d^2.</cmath>
+We apply the Pythagorean Law on <math>\triangle AOI</math> and <math>\triangle EFM</math> and get
+<cmath>d^2 = 4b^2 + OI^2, r^2 = \frac {25b^2}{4} + EF^2 \implies</cmath>
+<cmath>r = 3b\implies d = \frac {3a}{2} = \boxed {450}.</cmath>
+'''vladimir.shelomovskii@gmail.com, vvsss'''
+==Solution 7==
+Let <math>M</math> be the midpoint of <math>\overline{AB}</math> and <math>X</math> the center of <math>\triangle ABC</math>. Then <cmath>P, O, Q, M, X, C</cmath> all lie in the same vertical plane. We can make the following observations:
+* The equilateral triangle has side length <math>600</math>, so <math>MC=300\sqrt{3}</math> and <math>X</math> divides <math>MC</math> so that <math>MX=100\sqrt{3}</math> and <math>XC=200\sqrt{3}</math>;
+* <math>O</math> is the midpoint of <math>PQ</math> since <math>O</math> is equidistant from <math>A, B, C, P, Q</math> – it is also the circumcenter of <math>\triangle PCQ</math>;
+* <math>\angle PMQ=120^{\circ}</math>, the dihedral angle.
+To make calculations easier, we will denote <math>100\sqrt{3}=m</math>, so that <math>MX=m</math> and <math>XC=2m</math>.
+<asy>
+unitsize(20);
+pair P = (0, 12);
+pair Q = (0, -3);
+pair O = (P+Q)/2;
+pair M = (-3, 0);
+pair X = (0, 0);
+pair C = (6, 0);
+draw(P--O--Q);
+draw(M--X--C);
+draw(P--M--Q, blue);
+draw(Q--C--P);
+draw(circle((0, 4.5), 7.5));
+label("$P$", P, N);
+label("$Q$", Q, S);
+label("$O$", O, E);
+dot(O);
+label("$M$", M, W);
+label("$X$", X, NE);
+label("$C$", C, E);
+label("$m$", (M+X)/2, N);
+label("$2m$", (X+C)/2, N);
+</asy>
+Denote <math>PX=p</math> and <math>QX=q</math>, where the tangent addition formula on <math>\triangle PMQ</math> yields <cmath>\frac{\tan\measuredangle PMX+\tan\measuredangle QMX}{1-\tan\measuredangle PMX\tan\measuredangle QMX}=\tan(120^{\circ})=-\sqrt{3}.</cmath> Using <math>\tan\measuredangle PMX=\frac{p}{m}</math> and <math>\tan\measuredangle QMX=\frac{q}{m}</math>, we have <cmath>\frac{\frac{p}{m}+\frac{q}{m}}{1-\frac{p}{m}\cdot\frac{q}{m}}=-\sqrt{3}.</cmath> After multiplying both numerator and denominator by <math>m^{2}</math> we have <cmath>\frac{(p+q)m}{m^{2}-pq}=-\sqrt{3}.</cmath> But note that <math>pq=(2m)(2m)=4m^{2}</math> by power of a point at <math>X</math>, where we deduce by symmetry that <math>MM^{\prime}=MX=m</math> on the diagram below: <asy>
+unitsize(20);
+pair P = (0, 12);
+pair Q = (0, -3);
+pair O = (P+Q)/2;
+pair M = (-3, 0);
+pair Mprime = (-6, 0);
+pair X = (0, 0);
+pair C = (6, 0);
+draw(P--O--Q);
+draw(Mprime--M--X--C);
+draw(P--M--Q, blue);
+draw(Q--C--P);
+draw(circle((0, 4.5), 7.5));
+label("$P$", P, N);
+label("$Q$", Q, S);
+label("$O$", O, E);
+dot(O);
+label("$M$", M, S);
+label("$M^{\prime}$", Mprime, W);
+label("$X$", X, SE);
+label("$C$", C, E);
+label("$m$", (Mprime+M)/2, N);
+label("$m$", (M+X)/2, N);
+label("$2m$", (X+C)/2, N);
+</asy>
+Thus <cmath>\begin{align*} \frac{(p+q)m}{m^{2}-4m^{2}}=-\sqrt{3} \\ \frac{p+q}{-3m}=-\sqrt{3} \\ p+q=\left(-\sqrt{3}\right)\left(-3m\right) \\ p+q=3\sqrt{3}\cdot m.\end{align*}</cmath> Earlier we assigned the variable <math>m</math> to the length <math>100\sqrt{3}</math> which implies <math>PQ=\left(3\sqrt{3}\right)\left(100\sqrt{3}\right)=900</math>. Thus the distance <math>d</math> is equal to <math>\frac{PQ}{2}=\boxed{450}</math>.
+==Solution 8 (Law of Cosines)==
+Let <math>Z</math> be the center of <math>\triangle ABC</math>. Let <math>A’</math> be the midpoint of <math>BC</math>. Let <math>ZA’ = c = 100\sqrt{3}</math> and <math>ZA = 2c = 200\sqrt{3}</math>. Let <math>PZ = a</math> and <math>QZ = b</math>. We will be working in the plane that contains the points: <math>A</math>, <math>P</math>, <math>A’</math>, <math>Q</math>, <math>O</math>, and <math>Z</math>.
+Since <math>P</math>, <math>O</math>, and <math>Q</math> are collinear and <math>PO = QO = AO</math>, <math>\triangle PAQ</math> is a right triangle with <math>\angle PAQ = 90^{\circ}</math>. Since <math>AZ \perp PQ</math>, <math>(PZ)(QZ) = (AZ)^2 = ab = (2c)^2 = 120000</math>.
+<math>PA’ = \sqrt{a^2 + c^2}</math>, <math>QA’ = \sqrt{b^2 + c^2}</math>, <math>PQ = a + b</math>, and <math>\angle PAQ = 120^{\circ}</math>. By Law of Cosines <cmath>(a + b)^2 = a^2 + b^2 + 2c^2 + \sqrt{a^2b^2 + a^2c^2 + b^2c^2 + c^4}</cmath>. Substituting <math>4c^2</math> for <math>ab</math> and simplifying, we get <cmath>6c = \sqrt{17c^2 + a^2 + b^2}</cmath>. Squaring and simplifying, we get <cmath>a^2 + b^2 = 19c^2 = 570000</cmath>. Adding <math>2ab = 8c^2</math> to both sides we get <math>PQ = a + b = 900</math>. Since <math>O</math> is the midpoint of <math>PQ</math>, <math>d = PO = \boxed{450}</math>
+~numerophile
+==Solution 9 (Coordinate Bash)==
+Set <math>AB = s, M</math> as midpoint <math>BC, I</math> as the center of equilateral <math>\triangle ABC,</math> and by <math>30-60-90</math> triangle formulas, we know <math>IM = b = \frac {s}{2\sqrt{3}}, IA = IB = IC = \frac{s}{\sqrt{3}}</math>.
+First note that <math>P</math> and <math>Q</math> are on the line perpendicular to plane <math>ABC</math> through the circumcenter of <math>\triangle ABC</math>. Then notice that point <math>O</math> is the midpoint of <math>PQ</math>, so it also lies on this axis. Then, we see that the position of <math>O</math> relative to the triangle fully determines the positions of both <math>P</math> and <math>Q</math>, so setting the coordinates of <math>O</math> as <math>(0,0,h)</math> where the origin is defined the circumcenter and <math>\triangle ABC</math> lies in the <math>xy</math>-plane, we get: <cmath>\begin{align*} OA^2 = OB^2 = OC^2 = h^2+\frac{s^2}{3} = OP^2 = OQ^2 \end{align*}</cmath>
+Thus, the coordinates of <math>P</math> and <math>Q</math> are <math>(0,0,h\pm\sqrt{h^2+\frac{s^2}{3}})</math>. Now we make use of the angle condition. WLOG set the coordinates of <math>M</math> as <math>(\frac{s}{2\sqrt{3}},0,0)</math>. We know the angle between <math>PM</math> and <math>QM</math> is <math>120^{\circ}</math>, so after solving for the vectors, taking their dot product, equating it to <math>PM \cdot QM \cdot\cos{120^{\circ}}</math>, and <math>\textit{finally}</math> solving for <math>h</math> in terms of <math>s</math>, we get <cmath>\[
+h^2 = \frac{11}{48}s^2 \\
+\implies OA^2 = h^2 + \frac{s^2}{3} = \frac{27}{48}s^2 \\
+\implies OA = \frac{3}{4}s = \boxed{450}
+\]</cmath>
+(If someone feels like it, please feel free to fill in the rest of the details!)
+~ninjaforce
+==Video Solution by MOP 2024==
+https://youtu.be/hyhIlsAR2hs
+~r00tsOfUnity
+== See also ==
+{{AIME box|year=2016|n=II|num-b=13|num-a=15}}
+{{MAA Notice}}
+[[Category:Intermediate Geometry Problems]]
+[[Category:3D Geometry Problems]]

2016 AIME II (Problems • Answer Key • Resources)
Preceded by Problem 13	Followed by Problem 15
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search