Difference between revisions of "Trigonometric identities"

Revision as of 21:22, 11 March 2009

Trigonometric identities are used to manipulate trigonometry equations in certain ways. Here is a list of them:

Basic Definitions

The six basic trigonometric functions can be defined using a right triangle:

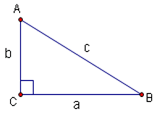
The six trig functions are sine, cosine, tangent, cosecant, secant, and cotangent. They are abbreviated by using the first three letters of their name (except for cosecant which uses $\csc$ ). They are defined as follows:

$\sin A = \frac ac$
$\csc A = \frac ca$
$\cos A = \frac bc$
$\sec A = \frac cb$
$\tan A = \frac ab$
$\cot A = \frac ba$

Even-Odd Identities

$\sin (-\theta) = -\sin (\theta)$

$\cos (-\theta) = \cos (\theta)$

$\tan (-\theta) = -\tan (\theta)$

$\csc (-\theta) = -\csc (\theta)$

$\sec (-\theta) = \sec (\theta)$

$\cot (-\theta) = -\cot (\theta)$

Reciprocal Relations

From the last section, it is easy to see that the following hold:

$\sin A = \frac 1{\csc A}$
$\cos A = \frac 1{\sec A}$
$\tan A = \frac 1{\cot A}$

Another useful identity that isn't a reciprocal relation is that $\tan A =\frac{\sin A}{\cos A}$ .

Note that $\sin^{-1} A \neq \csc A$ ; the former refers to the inverse trigonometric functions.

Pythagorean Identities

Using the Pythagorean Theorem on our triangle above, we know that $a^2 + b^2 = c^2$ . If we divide by $c^2$ we get $\left(\frac ac\right)^2 + \left(\frac bc\right)^2 = 1$ , which is just $\sin^2 A + \cos^2 A =1$ . Dividing by $a^2$ or $b^2$ instead produces two other similar identities. The Pythagorean Identities are listed below:

$\sin^2x + \cos^2x = 1$
$1 + \cot^2x = \csc^2x$
$\tan^2x + 1 = \sec^2x$

(Note that the second two are easily derived by dividing the first by $\cos^2x$ and $\sin^2x$ )

Angle Addition/Subtraction Identities

Once we have formulas for angle addition, angle subtraction is rather easy to derive. For example, we just look at $\sin(\alpha+(-\beta))$ and we can derive the sine angle subtraction formula using the sine angle addition formula.

$\sin(\alpha \pm \beta) = \sin \alpha\cos \beta \pm\sin \beta \cos \alpha$
$\cos(\alpha \pm \beta) = \cos \alpha \cos \beta \mp \sin \alpha \sin \beta$
$\tan(\alpha \pm \beta) = \frac{\tan \alpha \pm \tan \beta}{1\mp\tan \alpha \tan \beta}$

We can prove $\cos(\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta$ easily by using $\sin(\alpha + \beta) = \sin \alpha\cos \beta +\sin \beta \cos \alpha$ and $\sin(x)=\cos(90-x)$ .

$\cos (\alpha + \beta)$

$= \sin((90 -\alpha) - \beta)$ $= \sin (90- \alpha) \cos (\beta) - \sin ( \beta) \cos (90- \alpha)$

$=\cos \alpha \cos \beta - \sin \beta \sin \alpha$

Double Angle Identities

Double angle identities are easily derived from the angle addition formulas by just letting $\alpha = \beta$ . Doing so yields:

$\begin{eqnarray*} \sin 2\alpha &=& 2\sin \alpha \cos \alpha\\ \cos 2\alpha &=& \cos^2 \alpha - \sin^2 \alpha\\ &=& 2\cos^2 \alpha - 1\\ &=& 1-2\sin^2 \alpha\\ \tan 2\alpha &=& \frac{2\tan \alpha}{1-\tan^2\alpha}$ (Error compiling LaTeX. Unknown error_msg)

Half Angle Identities

Using the double angle identities, we can now derive half angle identities. The double angle formula for cosine tells us $\cos 2\alpha = 2\cos^2 \alpha - 1$ . Solving for $\cos \alpha$ we get $\cos \alpha =\pm \sqrt{\frac{1 + \cos 2\alpha}2}$ where we look at the quadrant of $\alpha$ to decide if it's positive or negative. Likewise, we can use the fact that $\cos 2\alpha = 1 - 2\sin^2 \alpha$ to find a half angle identity for sine. Then, to find a half angle identity for tangent, we just use the fact that $\tan \frac x2 =\frac{\sin \frac x2}{\cos \frac x2}$ and plug in the half angle identities for sine and cosine.

To summarize:

$\sin \frac{\theta}2 = \pm \sqrt{\frac{1-\cos \theta}2}$
$\cos \frac{\theta}2 = \pm \sqrt{\frac{1+\cos \theta}2}$
$\tan \frac{\theta}2 = \pm \sqrt{\frac{1-\cos \theta}{1+\cos \theta}}$

Prosthaphaeresis Identities

(Otherwise known as sum-to-product identities)

$\sin \theta \pm \sin \gamma = 2 \sin \frac{\theta\pm \gamma}2 \cos \frac{\theta\mp \gamma}2$
$\cos \theta + \cos \gamma = 2 \cos \frac{\theta+\gamma}2 \cos \frac{\theta-\gamma}2$
$\cos \theta - \cos \gamma = -2 \sin \frac{\theta+\gamma}2 \sin \frac{\theta-\gamma}2$

Law of Sines

Main article: Law of Sines

The extended Law of Sines states

$\frac a{\sin A} = \frac b{\sin B} = \frac c{\sin C} = 2R.$

Law of Cosines

Main article: Law of Cosines

The Law of Cosines states

$a^2 = b^2 + c^2 - 2bc\cos A.$

Law of Tangents

Main article: Law of Tangents

The Law of Tangents states that if $A$ and $B$ are angles in a triangle opposite sides $a$ and $b$ respectively, then

$\frac{\tan{\left(\frac{A-B}{2}\right)}}{\tan{\left(\frac{A+B}{2}\right)}}=\frac{a-b}{a+b} .$

Other Identities

$e^{i\theta} = \cos \theta + i\sin \theta$ (This is also written as $\text{cis }\theta$ )
$|1-e^{i\theta}|=2\sin\frac{\theta}{2}$

@@ Line 50: / Line 50: @@
 Once we have formulas for angle addition, angle subtraction is rather easy to derive.  For example, we just look at <math> \sin(\alpha+(-\beta))</math> and we can derive the sine angle subtraction formula using the sine angle addition formula.
-*<math> \sin(\alpha + \beta) = \sin \alpha\cos \beta +\sin \beta \cos \alpha</math> || <math>\sin(\alpha - \beta) = \sin \alpha \cos \beta - \sin \beta \cos \alpha</math>
+*<math> \sin(\alpha \pm \beta) = \sin \alpha\cos \beta \pm\sin \beta \cos \alpha</math>
-*<math> \cos(\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta </math> || <math>\cos(\alpha - \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta</math>
+*<math> \cos(\alpha \pm \beta) = \cos \alpha \cos \beta \mp \sin \alpha \sin \beta </math>
-*<math>\tan(\alpha + \beta) = \frac{\tan \alpha + \tan \beta}{1-\tan \alpha \tan \beta} </math> || <math>\tan(\alpha - \beta) = \frac{\tan \alpha - \tan \beta}{1+\tan \alpha \tan \beta} </math>
+*<math>\tan(\alpha \pm \beta) = \frac{\tan \alpha \pm \tan \beta}{1\mp\tan \alpha \tan \beta} </math>
 We can prove <math> \cos(\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta </math> easily by using <math> \sin(\alpha + \beta) = \sin \alpha\cos \beta +\sin \beta \cos \alpha</math> and <math>\sin(x)=\cos(90-x)</math>.
 <math>\cos (\alpha + \beta)</math>

Page

Toolbox

Search