Difference between revisions of "Mock USAMO by probability1.01 dropped problems"
(→Problem 2) |
Brut3Forc3 (talk | contribs) (→Problem 1) |
||
| Line 1: | Line 1: | ||
== Problem 1 == | == Problem 1 == | ||
| − | + | Let <math>n>1</math> be a fixed positive integer, and let <math>a_1,a_2,\ldots,a_n</math> be distinct positive integers. We define <math>S_k=a_1^k+a_2^k+\cdots+a_n^k</math>. Prove that there are no distinct positive integers <math>p,q,r</math> for which <math>S_p,S_q,S_r</math> is a geometric sequence. | |
[[Mock USAMO by probability1.01 dropped problems/Problem 1|Solution]] | [[Mock USAMO by probability1.01 dropped problems/Problem 1|Solution]] | ||
Revision as of 01:40, 16 May 2009
Problem 1
Let ![]() be a fixed positive integer, and let
be a fixed positive integer, and let ![]() be distinct positive integers. We define
be distinct positive integers. We define ![]() . Prove that there are no distinct positive integers
. Prove that there are no distinct positive integers ![]() for which
for which ![]() is a geometric sequence.
is a geometric sequence.
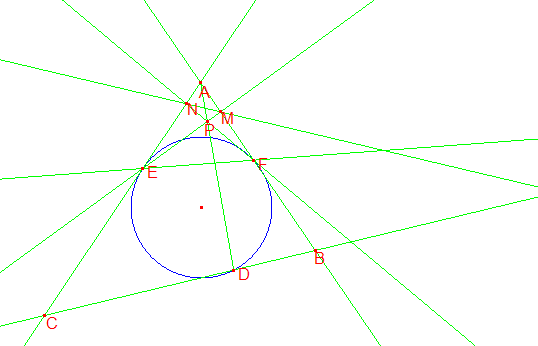
Problem 2
In triangle ![]() ,
, ![]() , let the incircle touch
, let the incircle touch ![]() ,
, ![]() , and
, and ![]() at
at ![]() ,
, ![]() , and
, and ![]() respectively. Let
respectively. Let ![]() be a point on
be a point on ![]() on the opposite
side of
on the opposite
side of ![]() from
from ![]() . If
. If ![]() and
and ![]() meet at
meet at ![]() , and
, and ![]() and
and ![]() meet
at
meet
at ![]() , prove that
, prove that ![]() ,
, ![]() , and
, and ![]() concur.
Reason: The whole incircle business seemed rather artificial. Besides, it wasn’t that difficult.
concur.
Reason: The whole incircle business seemed rather artificial. Besides, it wasn’t that difficult.