Difference between revisions of "1988 AIME Problems/Problem 12"
(→Solution 2) |
m (→Solution 2) |
||
| Line 25: | Line 25: | ||
==Solution 2== | ==Solution 2== | ||
| − | Let | + | Let <math>A,B,C</math> be the weights of the respective vertices. We see that the weights of the feet of the cevians are <math>A+B,B+C,C+A</math>. By [[mass points]], we have that: <cmath>\dfrac{a}{3}=\dfrac{B+C}{A}</cmath> <cmath>\dfrac{b}{3}=\dfrac{C+A}{B}</cmath> <cmath>\dfrac{c}{3}=\dfrac{A+B}{C}</cmath> |
If we add the equations together, we get <math>\frac{a+b+c}{3}=\frac{A^2B+A^2C+B^2A+B^2C+C^2A+C^2B}{ABC}=\frac{43}{3}</math> | If we add the equations together, we get <math>\frac{a+b+c}{3}=\frac{A^2B+A^2C+B^2A+B^2C+C^2A+C^2B}{ABC}=\frac{43}{3}</math> | ||
Revision as of 18:32, 16 March 2017
Contents
[hide]Problem
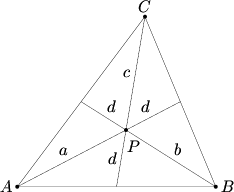
Let ![]() be an interior point of triangle
be an interior point of triangle ![]() and extend lines from the vertices through
and extend lines from the vertices through ![]() to the opposite sides. Let
to the opposite sides. Let ![]() ,
, ![]() ,
, ![]() , and
, and ![]() denote the lengths of the segments indicated in the figure. Find the product
denote the lengths of the segments indicated in the figure. Find the product ![]() if
if ![]() and
and ![]() .
.
Solution 1
Call the cevians AD, BE, and CF. Using area ratios (![]() and
and ![]() have the same base), we have:
have the same base), we have:
![]()
Similarily, ![]() and
and ![]() .
.
Then,
![]()
The identity ![]() is a form of Ceva's Theorem.
is a form of Ceva's Theorem.
Plugging in ![]() , we get
, we get
![]()
![]()
![]()
![]()
Solution 2
Let ![]() be the weights of the respective vertices. We see that the weights of the feet of the cevians are
be the weights of the respective vertices. We see that the weights of the feet of the cevians are ![]() . By mass points, we have that:
. By mass points, we have that: ![]()
![]()
![]()
If we add the equations together, we get ![]()
If we multiply them together, we get ![]()
See also
| 1988 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 11 |
Followed by Problem 13 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.