Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Mock USAMO by probability1.01 dropped problems"

(→‎Problem 2)
(→‎Problem 2)
Line 10: Line 10:
 
at <math>N</math>, prove that <math>MN, EF, and BC</math> concur.
 
at <math>N</math>, prove that <math>MN, EF, and BC</math> concur.
 
''Reason: The whole incircle business seemed rather artificial. Besides, it wasn’t that difficult.''
 
''Reason: The whole incircle business seemed rather artificial. Besides, it wasn’t that difficult.''
 +
 
[[Image:Mock_usamo.png]]
 
[[Image:Mock_usamo.png]]
 +
 
[[Mock USAMO by probability1.01 dropped problems/Problem 2|Solution]]
 
[[Mock USAMO by probability1.01 dropped problems/Problem 2|Solution]]
  

Revision as of 15:45, 2 September 2006

Problem 1

Solution

Problem 2

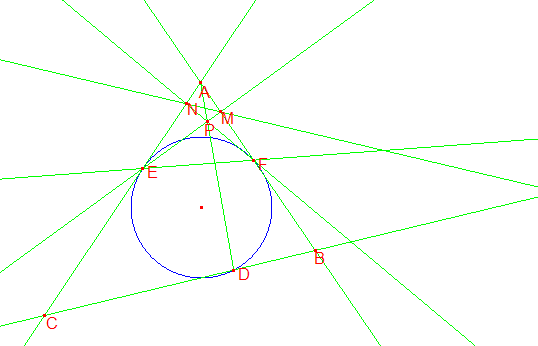
In triangle $ABC$, $AB \not= AC$, let the incircle touch $BC$, $CA$, and $AB$ at $D$, $E$, and $F$ respectively. Let $P$ be a point on $AD$ on the opposite side of $EF$ from $D$. If $EP$ and $AB$ meet at $M$, and $FP$ and $AC$ meet at $N$, prove that $MN, EF, and BC$ concur. Reason: The whole incircle business seemed rather artificial. Besides, it wasn’t that difficult.

Mock usamo.png

Solution

Problem 3

Solution

Problem 4

Solution

Problem 5

Solution

Problem 6

Solution

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Mock_USAMO_by_probability1.01_dropped_problems&oldid=9974"