Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2019 USAMO Problems/Problem 2"

(→‎Solution)
(→‎Solution)
 
(14 intermediate revisions by 3 users not shown)
Line 6: Line 6:
 
Let <math>PE \cap DC = M</math>. Also, let <math>N</math> be the midpoint of <math>AB</math>.
 
Let <math>PE \cap DC = M</math>. Also, let <math>N</math> be the midpoint of <math>AB</math>.
 
Note that only one point <math>P</math> satisfies the given angle condition. With this in mind, construct <math>P'</math> with the following properties:
 
Note that only one point <math>P</math> satisfies the given angle condition. With this in mind, construct <math>P'</math> with the following properties:
−
[list]
+
−
[*] <math>AP' \cdot AB = AD^2</math>
+
(1) <math>AP' \cdot AB = AD^2</math>
−
[*] <math>BP' \cdot AB = CD^2</math>
+
 
−
[/list]
+
(2) <math>BP' \cdot AB = CD^2</math>
−
[b]Claim:[/b]<math>P = P'</math>
+
−
[i]Proof:[/i]
+
Claim: <math>P = P'</math>
 +
 
 +
Proof:
 
The conditions imply the similarities <math>ADP \sim ABD</math> and <math>BCP \sim BAC</math> whence <math>\measuredangle APD = \measuredangle BDA = \measuredangle BCA = \measuredangle CPB</math> as desired. <math>\square</math>
 
The conditions imply the similarities <math>ADP \sim ABD</math> and <math>BCP \sim BAC</math> whence <math>\measuredangle APD = \measuredangle BDA = \measuredangle BCA = \measuredangle CPB</math> as desired. <math>\square</math>
−
[b]Claim:[/b] <math>PE</math> is a symmedian in <math>AEB</math>
+
 
−
[i]Proof:[/i]
+
Claim: <math>PE</math> is a symmedian in <math>AEB</math>
 +
 
 +
Proof:
 
We have  
 
We have  
−
\begin{align*}  
+
<cmath>\begin{align*}  
 
AP \cdot AB = AD^2 \iff AB^2 \cdot AP &= AD^2 \cdot AB \\
 
AP \cdot AB = AD^2 \iff AB^2 \cdot AP &= AD^2 \cdot AB \\
 
\iff \left( \frac{AB}{AD} \right)^2 &= \frac{AB}{AP} \\
 
\iff \left( \frac{AB}{AD} \right)^2 &= \frac{AB}{AP} \\
Line 22: Line 26:
 
\iff \frac{AB^2 - AD^2}{AD^2} &= \frac{BP}{AP} \\
 
\iff \frac{AB^2 - AD^2}{AD^2} &= \frac{BP}{AP} \\
 
\iff \left(\frac{BC}{AD} \right)^2 &= \left(\frac{BE}{AE} \right)^2 = \frac{BP}{AP}  
 
\iff \left(\frac{BC}{AD} \right)^2 &= \left(\frac{BE}{AE} \right)^2 = \frac{BP}{AP}  
−
\end{align*}
+
\end{align*}</cmath>
 
as desired. <math>\square</math>
 
as desired. <math>\square</math>
 +
 
Since <math>P</math> is the isogonal conjugate of <math>N</math>, <math>\measuredangle PEA = \measuredangle MEC = \measuredangle BEN</math>. However <math>\measuredangle MEC = \measuredangle BEN</math> implies that <math>M</math> is the midpoint of <math>CD</math> from similar triangles, so we are done. <math>\square</math>
 
Since <math>P</math> is the isogonal conjugate of <math>N</math>, <math>\measuredangle PEA = \measuredangle MEC = \measuredangle BEN</math>. However <math>\measuredangle MEC = \measuredangle BEN</math> implies that <math>M</math> is the midpoint of <math>CD</math> from similar triangles, so we are done. <math>\square</math>
  
−
{{MAA Notice}}
+
==Solution 2==
 +
[[File:2019 USAMO 2.png|450px|right]]
 +
[[File:2019 USAMO 2a.png|450px|right]]
 +
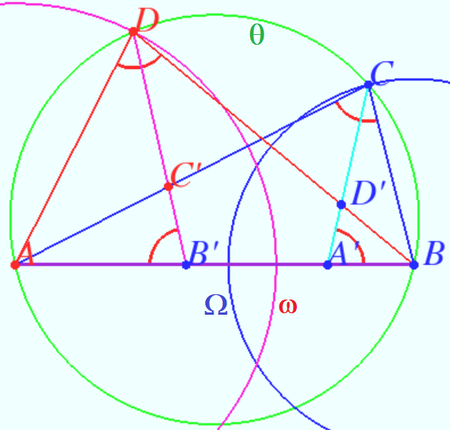
Let <math>\omega</math> be the circle centered at <math>A</math> with radius <math>AD.</math>
 +
 
 +
Let <math>\Omega</math> be the circle centered at <math>B</math> with radius <math>BC.</math>
 +
 
 +
We denote <math>I_\omega</math> and <math>I_\Omega</math> inversion with respect to <math>\omega</math> and <math>\Omega,</math> respectively.
 +
<cmath>B'= I_\omega (B), C'= I_\omega (C), D = I_\omega (D) \implies</cmath>
 +
<cmath>AB' \cdot AB = AD^2,  \angle ACB = \angle AB'C'.</cmath>
 +
<cmath>A'= I_\Omega (A), D'= I_\Omega (D), C = I_\Omega (C) \implies</cmath>
 +
<cmath>BA' \cdot AB = BC^2,  \angle BDA = \angle BA'D'.</cmath>
 +
Let <math>\theta</math> be the circle <math>ABCD.</math>
 +
 
 +
<math>I_\omega (\theta) = B'C'D,</math> straight line, therefore <cmath>\angle AB'C' = \angle AB'D' = \angle ACB.</cmath>
 +
<math>I_\Omega (\theta) = A'D'C,</math> straight line, therefore
 +
<cmath>\angle BA'D' = \angle BA'C = \angle BDA.</cmath>
 +
<math>ABCD</math> is cyclic <math>\implies \angle BA'C = \angle AB'D.</math>
 +
<cmath>AB' + BA' = \frac {AD^2 + BC^2 }{AB} = AB \implies</cmath> points <math>A'</math> and <math>B'</math> are coincide.
 +
 
 +
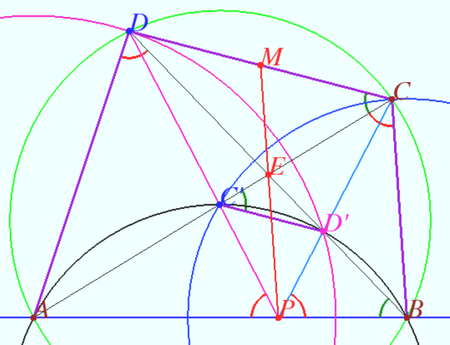
Denote <math>A' = B' = Q \in AB.</math>
 +
 
 +
Suppose, we move point <math>Q</math> from <math>A</math> to <math>B.</math> Then <math>\angle AQD</math> decreases monotonically, <math>\angle BQC</math> increases monotonically. So, there is only one point where <cmath>\angle AQD = \angle BQC \implies P = Q.</cmath>
 +
 
 +
<cmath>B = I_\omega (P), D' = I_\omega (D'), C' = I_\omega (C), A = I_\omega (\infty) \implies</cmath>
 +
<math>\hspace{19mm} I_\omega (CD'P) = AC'D'B</math> is cyclic.
 +
<cmath>\angle ACD = \angle ABD = \angle CC'D \implies C' D' || CD \implies</cmath>
 +
<math>\hspace{19mm} C'D'CD</math> is  trapezoid.
 +
 
 +
It is known that the intersection of the diagonals, intersection point of the lines containing the lateral sides of the trapezoid and the midpoints of two parallel sides are collinear.
 +
 
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
  
 
==See also==
 
==See also==
 
{{USAMO newbox|year=2019|num-b=1|num-a=3}}
 
{{USAMO newbox|year=2019|num-b=1|num-a=3}}
 +
 +
{{MAA Notice}}

Latest revision as of 21:51, 18 October 2022

Problem

Let $ABCD$ be a cyclic quadrilateral satisfying $AD^2 + BC^2 = AB^2$. The diagonals of $ABCD$ intersect at $E$. Let $P$ be a point on side $\overline{AB}$ satisfying $\angle APD = \angle BPC$. Show that line $PE$ bisects $\overline{CD}$.

Solution

Let $PE \cap DC = M$. Also, let $N$ be the midpoint of $AB$. Note that only one point $P$ satisfies the given angle condition. With this in mind, construct $P'$ with the following properties:

(1) $AP' \cdot AB = AD^2$

(2) $BP' \cdot AB = CD^2$

Claim: $P = P'$

Proof: The conditions imply the similarities $ADP \sim ABD$ and $BCP \sim BAC$ whence $\measuredangle APD = \measuredangle BDA = \measuredangle BCA = \measuredangle CPB$ as desired. $\square$

Claim: $PE$ is a symmedian in $AEB$

Proof: We have \begin{align*} AP \cdot AB = AD^2 \iff AB^2 \cdot AP &= AD^2 \cdot AB \\ \iff \left( \frac{AB}{AD} \right)^2 &= \frac{AB}{AP} \\ \iff \left( \frac{AB}{AD} \right)^2 - 1 &= \frac{AB}{AP} - 1 \\ \iff \frac{AB^2 - AD^2}{AD^2} &= \frac{BP}{AP} \\ \iff \left(\frac{BC}{AD} \right)^2 &= \left(\frac{BE}{AE} \right)^2 = \frac{BP}{AP} \end{align*} as desired. $\square$

Since $P$ is the isogonal conjugate of $N$, $\measuredangle PEA = \measuredangle MEC = \measuredangle BEN$. However $\measuredangle MEC = \measuredangle BEN$ implies that $M$ is the midpoint of $CD$ from similar triangles, so we are done. $\square$

Solution 2

2019 USAMO 2.png
2019 USAMO 2a.png

Let $\omega$ be the circle centered at $A$ with radius $AD.$

Let $\Omega$ be the circle centered at $B$ with radius $BC.$

We denote $I_\omega$ and $I_\Omega$ inversion with respect to $\omega$ and $\Omega,$ respectively. \[B'= I_\omega (B), C'= I_\omega (C), D = I_\omega (D) \implies\] \[AB' \cdot AB = AD^2, \angle ACB = \angle AB'C'.\] \[A'= I_\Omega (A), D'= I_\Omega (D), C = I_\Omega (C) \implies\] \[BA' \cdot AB = BC^2, \angle BDA = \angle BA'D'.\] Let $\theta$ be the circle $ABCD.$

$I_\omega (\theta) = B'C'D,$ straight line, therefore \[\angle AB'C' = \angle AB'D' = \angle ACB.\] $I_\Omega (\theta) = A'D'C,$ straight line, therefore \[\angle BA'D' = \angle BA'C = \angle BDA.\] $ABCD$ is cyclic $\implies \angle BA'C = \angle AB'D.$ \[AB' + BA' = \frac {AD^2 + BC^2 }{AB} = AB \implies\] points $A'$ and $B'$ are coincide.

Denote $A' = B' = Q \in AB.$

Suppose, we move point $Q$ from $A$ to $B.$ Then $\angle AQD$ decreases monotonically, $\angle BQC$ increases monotonically. So, there is only one point where \[\angle AQD = \angle BQC \implies P = Q.\]

\[B = I_\omega (P), D' = I_\omega (D'), C' = I_\omega (C), A = I_\omega (\infty) \implies\] $\hspace{19mm} I_\omega (CD'P) = AC'D'B$ is cyclic. \[\angle ACD = \angle ABD = \angle CC'D \implies C' D' || CD \implies\] $\hspace{19mm} C'D'CD$ is trapezoid.

It is known that the intersection of the diagonals, intersection point of the lines containing the lateral sides of the trapezoid and the midpoints of two parallel sides are collinear.

vladimir.shelomovskii@gmail.com, vvsss

See also

2019 USAMO (Problems • Resources)
Preceded by
Problem 1 		Followed by
Problem 3
1 • 2 • 3 • 4 • 5 • 6
All USAMO Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2019_USAMO_Problems/Problem_2&oldid=179229"