Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2019 IMO Problems/Problem 6"

(→‎Problem)
 
(11 intermediate revisions by 3 users not shown)
Line 1: Line 1:
 
==Problem==
 
==Problem==
−
Let <math>I</math> be the incenter of acute triangle <math>ABC</math> with <math>AB \neq AC</math>. The incircle ω of <math>ABC</math> is tangent to sides <math>BC</math>, <math>CA</math>, and <math>AB</math> at <math>D</math>, <math>E</math>, and <math>F</math>, respectively. The line through <math>D</math> perpendicular to <math>EF</math> meets ω again at <math>R</math>. Line <math>AR</math> meets ω again at <math>P</math>. The circumcircles of triangles <math>PCE</math> and <math>PBF</math> meet again at <math>Q</math>.
+
Let <math>I</math> be the incenter of acute triangle <math>ABC</math> with <math>AB \neq AC</math>. The incircle <math>\omega</math> of <math>ABC</math> is tangent to sides <math>BC</math>, <math>CA</math>, and <math>AB</math> at <math>D</math>, <math>E</math>, and <math>F</math>, respectively. The line through <math>D</math> perpendicular to <math>EF</math> meets <math>\omega</math> again at <math>R</math>. Line <math>AR</math> meets ω again at <math>P</math>. The circumcircles of triangles <math>PCE</math> and <math>PBF</math> meet again at <math>Q</math>.
 
Prove that lines <math>DI</math> and <math>PQ</math> meet on the line through <math>A</math> perpendicular to <math>AI</math>.
 
Prove that lines <math>DI</math> and <math>PQ</math> meet on the line through <math>A</math> perpendicular to <math>AI</math>.
 +
 +
==Solution==
 +
[[File:2019 6 s1.png|450px|right]]
 +
[[File:2019 6 s2.png|450px|right]]
 +
[[File:2019 6 s3.png|390px|right]]
 +
[[File:2019 6 s4.png|390px|right]]
 +
<i><b>Step 1</b></i>
 +
 +
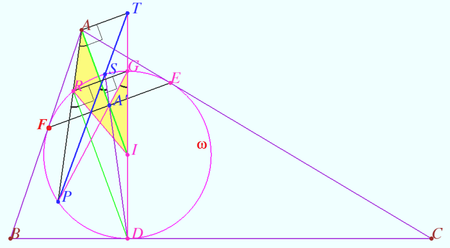
We find an auxiliary point <math>S.</math>
 +
 +
Let <math>G</math> be the antipode of <math>D</math> on <math>\omega, GD = 2R,</math> where <math>R</math> is radius <math>\omega.</math>
 +
 +
We define <math>A' = PG \cap AI.</math>
 +
 +
<math>RD||AI, PRGD</math> is cyclic <math>\implies \angle IAP = \angle DRP = \angle DGP.</math>
 +
 +
<math>RD||AI, RD \perp RG, RI=GI \implies \angle AIR = \angle AIG  \implies</math>
 +
<cmath>\triangle AIR \sim \triangle GIA' \implies  \frac {AI}{GI} = \frac {RI}{A'I}\implies A'I \cdot AI = R^2.</cmath>
 +
An inversion with respect <math>\omega</math> swap <math>A</math> and <math>A' \implies A'</math> is the midpoint <math>EF.</math>
 +
 +
Let <math>DA'</math> meets <math>\omega</math> again at <math>S.</math> We define <math>T = PS \cap DI.</math>
 +
 +
Opposite sides of any quadrilateral inscribed in the circle <math>\omega</math> meet on the polar line of the intersection of the diagonals with respect to <math>\omega \implies DI</math> and <math>PS</math> meet on the line through <math>A</math> perpendicular to <math>AI.</math>
 +
The problem is reduced to proving that <math>Q \in PST.</math>
 +
 +
<i><b>Step 2</b></i>
 +
 +
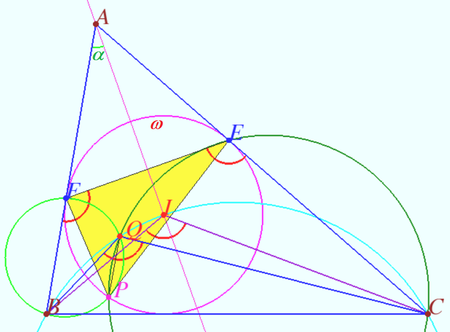
We find a simplified way to define the point <math>Q.</math>
 +
 +
We define <math>\angle BAC = 2 \alpha \implies \angle AFE = \angle AEF = 90^\circ – \alpha \implies</math>
 +
<math>\angle BFE = \angle CEF = 180^\circ – (90^\circ – \alpha) = 90^\circ + \alpha =  \angle BIC</math>
 +
<math>(AI, BI,</math> and <math>CI</math> are bisectrices).
 +
 +
We use the Tangent-Chord Theorem and get <cmath>\angle EPF = \angle AEF = 90^\circ – \alpha.</cmath>
 +
 +
<math>\angle BQC =  \angle BQP +  \angle PQC = \angle BFP + \angle CEP =</math>
 +
<math>=\angle BFE – \angle EFP + \angle CEF – \angle FEP =</math>
 +
<math>= 90^\circ + \alpha + 90^\circ + \alpha – (90^\circ + \alpha) = </math>
 +
<math>90^\circ + \alpha = \angle BIC \implies</math>
 +
 +
Points <math>Q, B, I,</math> and <math>C</math> are concyclic.
 +
 +
<i><b>Step 3</b></i>
 +
 +
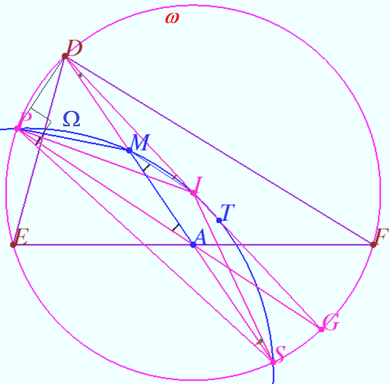
We perform inversion around <math>\omega.</math> The straight line <math>PST</math> maps onto circle <math>PITS.</math> We denote this circle <math>\Omega.</math> We prove that the midpoint of <math>AD</math> lies on the circle <math>\Omega.</math>
 +
 +
In the diagram, the configuration under study is transformed using inversion with respect to <math>\omega.</math> The images of the points are labeled in the same way as the points themselves. Points <math>D,E,F,P,S,</math> and <math>G</math> have saved their position. Vertices <math>A, B,</math> and <math>C</math> have moved to the midpoints of the segments <math>EF, FD,</math> and <math>DE,</math> respectively.
 +
 +
Let <math>M</math> be the midpoint <math>AD.</math>
 +
 +
We define <math>\angle MID = \beta, \angle MDI = \gamma \implies</math>
 +
<math>\angle IMA = \angle MID + \angle MDI = \beta + \gamma = \varphi.</math>
 +
<math>DI = IS \implies \angle ISD = \gamma.</math>
 +
 +
<math>MI</math> is triangle <math>DAG</math> midline <math>\implies MI || AG \implies</math>
 +
<cmath>MI || PG \implies \angle MAP = \angle AMI =  \varphi.</cmath>
 +
<cmath>\angle DPA = 90^\circ \implies PM = MA \implies</cmath>
 +
<cmath>\angle PMA = \angle PMS = 180^\circ – 2 \varphi.</cmath>
 +
<math>PI = IS \implies \angle PIS = 180^\circ – 2 \varphi =\angle DPA \implies</math> point <math>M</math> lies on <math>\Omega.</math>
 +
<math>ABDC</math> is parallelogram <math>\implies M</math> is midpoint <math>BC.</math>
 +
 +
<i><b>Step 4</b></i>
 +
 +
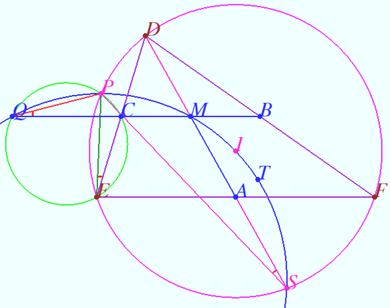
We prove that image of <math>Q</math> lies on <math>\Omega.</math>
 +
 +
In the inversion plane the image of point <math>Q</math> lies on straight line <math>BC</math> (It is image of circle <math>BIC)</math> and on circle <math>PCE.</math>
 +
 +
<cmath>\angle PQM = \angle PQC =  \angle PEC = \angle PED = \angle PSD = \angle PSM \implies</cmath> point <math>Q</math> lies on <math>\Omega</math>.
 +
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
 +
==See Also==
 +
 +
{{IMO box|year=2019|num-b=5|after=Last Problem}}

Latest revision as of 00:52, 19 November 2023

Problem

Let $I$ be the incenter of acute triangle $ABC$ with $AB \neq AC$. The incircle $\omega$ of $ABC$ is tangent to sides $BC$, $CA$, and $AB$ at $D$, $E$, and $F$, respectively. The line through $D$ perpendicular to $EF$ meets $\omega$ again at $R$. Line $AR$ meets ω again at $P$. The circumcircles of triangles $PCE$ and $PBF$ meet again at $Q$. Prove that lines $DI$ and $PQ$ meet on the line through $A$ perpendicular to $AI$.

Solution

2019 6 s1.png
2019 6 s2.png
2019 6 s3.png
2019 6 s4.png

Step 1

We find an auxiliary point $S.$

Let $G$ be the antipode of $D$ on $\omega, GD = 2R,$ where $R$ is radius $\omega.$

We define $A' = PG \cap AI.$

$RD||AI, PRGD$ is cyclic $\implies \angle IAP = \angle DRP = \angle DGP.$

$RD||AI, RD \perp RG, RI=GI \implies \angle AIR = \angle AIG \implies$ \[\triangle AIR \sim \triangle GIA' \implies \frac {AI}{GI} = \frac {RI}{A'I}\implies A'I \cdot AI = R^2.\] An inversion with respect $\omega$ swap $A$ and $A' \implies A'$ is the midpoint $EF.$

Let $DA'$ meets $\omega$ again at $S.$ We define $T = PS \cap DI.$

Opposite sides of any quadrilateral inscribed in the circle $\omega$ meet on the polar line of the intersection of the diagonals with respect to $\omega \implies DI$ and $PS$ meet on the line through $A$ perpendicular to $AI.$ The problem is reduced to proving that $Q \in PST.$

Step 2

We find a simplified way to define the point $Q.$

We define $\angle BAC = 2 \alpha \implies \angle AFE = \angle AEF = 90^\circ – \alpha \implies$ $\angle BFE = \angle CEF = 180^\circ – (90^\circ – \alpha) = 90^\circ + \alpha = \angle BIC$ $(AI, BI,$ and $CI$ are bisectrices).

We use the Tangent-Chord Theorem and get \[\angle EPF = \angle AEF = 90^\circ – \alpha.\]

$\angle BQC = \angle BQP + \angle PQC = \angle BFP + \angle CEP =$ $=\angle BFE – \angle EFP + \angle CEF – \angle FEP =$ $= 90^\circ + \alpha + 90^\circ + \alpha – (90^\circ + \alpha) =$ $90^\circ + \alpha = \angle BIC \implies$

Points $Q, B, I,$ and $C$ are concyclic.

Step 3

We perform inversion around $\omega.$ The straight line $PST$ maps onto circle $PITS.$ We denote this circle $\Omega.$ We prove that the midpoint of $AD$ lies on the circle $\Omega.$

In the diagram, the configuration under study is transformed using inversion with respect to $\omega.$ The images of the points are labeled in the same way as the points themselves. Points $D,E,F,P,S,$ and $G$ have saved their position. Vertices $A, B,$ and $C$ have moved to the midpoints of the segments $EF, FD,$ and $DE,$ respectively.

Let $M$ be the midpoint $AD.$

We define $\angle MID = \beta, \angle MDI = \gamma \implies$ $\angle IMA = \angle MID + \angle MDI = \beta + \gamma = \varphi.$ $DI = IS \implies \angle ISD = \gamma.$

$MI$ is triangle $DAG$ midline $\implies MI || AG \implies$ \[MI || PG \implies \angle MAP = \angle AMI = \varphi.\] \[\angle DPA = 90^\circ \implies PM = MA \implies\] \[\angle PMA = \angle PMS = 180^\circ – 2 \varphi.\] $PI = IS \implies \angle PIS = 180^\circ – 2 \varphi =\angle DPA \implies$ point $M$ lies on $\Omega.$ $ABDC$ is parallelogram $\implies M$ is midpoint $BC.$

Step 4

We prove that image of $Q$ lies on $\Omega.$

In the inversion plane the image of point $Q$ lies on straight line $BC$ (It is image of circle $BIC)$ and on circle $PCE.$

\[\angle PQM = \angle PQC = \angle PEC = \angle PED = \angle PSD = \angle PSM \implies\] point $Q$ lies on $\Omega$.

vladimir.shelomovskii@gmail.com, vvsss

See Also

2019 IMO (Problems) • Resources
Preceded by
Problem 5 		1 • 2 • 3 • 4 • 5 • 6 Followed by
Last Problem
All IMO Problems and Solutions
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2019_IMO_Problems/Problem_6&oldid=204597"