Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1988 AIME Problems/Problem 6"

(→‎See also)
m
 
(20 intermediate revisions by 9 users not shown)
Line 1: Line 1:
 +
__TOC__
 +
 
== Problem ==
 
== Problem ==
 +
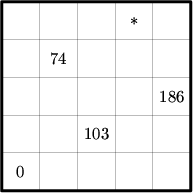
It is possible to place positive integers into the vacant twenty-one squares of the <math>5 \times 5</math> square shown below so that the numbers in each row and column form arithmetic sequences.  Find the number that must occupy the vacant square marked by the asterisk (*).
 +
 +
[[Image:1988_AIME-6.png]]
 +
 +
== Solutions ==
 +
=== Solution 1 (specific) ===
 +
Let the coordinates of the square at the bottom left be <math>(0,0)</math>, the square to the right <math>(1,0)</math>, etc.
 +
 +
Label the leftmost column (from bottom to top) <math>0, a, 2a, 3a, 4a</math> and the bottom-most row (from left to right) <math>0, b, 2b, 3b, 4b</math>. Our method will be to use the given numbers to set up equations to solve for <math>a</math> and <math>b</math>, and then calculate <math>(*)</math>.
 +
 +
<math>\begin{tabular}[b]{|c|c|c|c|c|}\hline 4a & & & * & \\
 +
\hline 3a & 74 & & & \\
 +
\hline 2a & & & & 186 \\
 +
\hline a & & 103 & & \\
 +
\hline 0 & b & 2b & 3b & 4b \\
 +
\hline \end{tabular}</math>
 +
 +
We can compute the squares at the intersections of two existing numbers in terms of <math>a</math> and <math>b</math>; two such equations will give us the values of <math>a</math> and <math>b</math>. On the fourth row from the bottom, the common difference is <math>74 - 3a</math>, so the square at <math>(2,3)</math> has a value of <math>148 - 3a</math>. On the third column from the left, the common difference is <math>103 - 2b</math>, so that square also has a value of <math>2b + 3(103 - 2b) = 309 - 4b</math>. Equating, we get <math>148 - 3a = 309 - 4b \Longrightarrow 4b - 3a = 161</math>.
 +
 +
Now we compute the square <math>(2,2)</math>. By rows, this value is simply the average of <math>2a</math> and <math>186</math>, so it is equal to <math>\frac{2a + 186}{2} = a + 93</math>. By columns, the common difference is <math>103 - 2b</math>, so our value is <math>206 - 2b</math>. Equating, <math>a + 93 = 206 - 2b \Longrightarrow a + 2b = 113</math>.
 +
 +
Solving
 +
<cmath>
 +
\begin{align*}4b - 3a &= 161\\
 +
a + 2b &= 113
 +
\end{align*}
 +
</cmath>
 +
 +
gives <math>a = 13</math>, <math>b = 50</math>. Now it is simple to calculate <math>(4,3)</math>. One way to do it is to see that <math>(2,2)</math> has <math>206 - 2b = 106</math> and <math>(4,2)</math> has <math>186</math>, so <math>(3,2)</math> has <math>\frac{106 + 186}{2} = 146</math>. Now, <math>(3,0)</math> has <math>3b = 150</math>, so <math>(3,2) = \frac{(3,0) + (3,4)}{2} \Longrightarrow (3,4) = * = \boxed{142}</math>.
 +
 +
=== Solution 2 (general) ===
 +
First, let <math>a =</math> the number to be placed in the first column, fourth row.  Let <math>b =</math> the number to be placed in the second column, fifth row.  We can determine the entire first column and fifth row in terms of <math>a</math> and <math>b</math>:
 +
 +
<math>\begin{tabular}[b]{|c|c|c|c|c|}\hline 4a & & & & \\
 +
\hline 3a & & & & \\
 +
\hline 2a & & & & \\
 +
\hline a & & & & \\
 +
\hline 0 & b & 2b & 3b & 4b \\
 +
\hline \end{tabular}</math>
 +
 +
Next, let <math>a + b + c =</math> the number to be placed in the second column, fourth row.  We can determine the entire second column and fourth row in terms of <math>a</math>, <math>b</math>, and <math>c</math>:
 +
 +
<math>\begin{tabular}[b]{|c|c|c|c|c|}\hline 4a & 4a + b + 4c & & & \\
 +
\hline 3a & 3a + b + 3c & & & \\
 +
\hline 2a & 2a + b + 2c & & & \\
 +
\hline a & a + b + c & a + 2b + 2c & a + 3b + 3c & a + 4b + 4c \\
 +
\hline 0 & b & 2b & 3b & 4b \\
 +
\hline \end{tabular}</math>
 +
 +
We have now determined at least two values in each row and column.  We can finish the table without introducing any more variables:
 +
 +
<math>\begin{tabular}[b]{|c|c|c|c|c|}\hline 4a & 4a + b + 4c & 4a + 2b + 8c & 4a + 3b + 12c & 4a + 4b + 16c \\
 +
\hline 3a & 3a + b + 3c & 3a + 2b + 6c & 3a + 3b + 9c & 3a + 4b + 12c \\
 +
\hline 2a & 2a + b + 2c & 2a + 2b + 4c & 2a + 3b + 6c & 2a + 4b + 8c \\
 +
\hline a & a + b + c & a + 2b + 2c & a + 3b + 3c & a + 4b + 4c \\
 +
\hline 0 & b & 2b & 3b & 4b \\
 +
\hline \end{tabular}</math>
 +
 +
We now have a system of equations.
 +
 +
<div style="text-align:center;"><math>3a + b + 3c = 74</math><br />
 +
<math>2a + 4b + 8c = 186</math><br />
 +
<math>a + 2b + 2c = 103</math></div>
 +
 +
Solving, we find that <math>(a,b,c) = (13,50, - 5)</math>.  The number in the square marked by the asterisk is <math>4a + 3b + 12c = \boxed{142}</math>
 +
 +
==Solution 3 (Only one variable)==
 +
We begin with the table that was given to us and add in the following arithmetic progression on the bottom:
 +
 +
<math>\begin{tabular}[b]{|c|c|c|c|c|}\hline & & & * & \\
 +
\hline & 74 & & & \\
 +
\hline & & & & 186 \\
 +
\hline & & 103 & & \\
 +
\hline 0 & x & 2x & 3x & 4x \\
 +
\hline \end{tabular}</math>
 +
 +
Since all the rows and columns satisfy an arithmetic progression, we have the following:
 +
 +
<math>\begin{tabular}[b]{|c|c|c|c|c|}\hline & & 412 - 6x & 392 - 5x & 372 - 4x \\
 +
\hline & 74 & 309 - 4x  & 294 - 3x  & 279 - 2x \\
 +
\hline & & 206 - 2x & 196 - x & 186 \\
 +
\hline & & 103 & 98 + x & 2x + 93 \\
 +
\hline 0 & x & 2x & 3x & 4x \\
 +
\hline \end{tabular}</math>
  
−
== Solution ==
+
We can solve for <math>x</math> in the 2nd row, namely <math>324 - 5x = 74</math> because the arithmetic progression from left to right has difference <math>x - 15</math>. Therefore, we have <math>x = 50</math>, and because the desired asterisk is <math>392 - 5x</math>, the answer is <math>392 - 250</math> = <math>\boxed {142}</math>.
 +
 
 +
~Arcticturn
  
 
== See also ==
 
== See also ==
−
* [[1988 AIME Problems]]
 
−
 
 
{{AIME box|year=1988|num-b=5|num-a=7}}
 
{{AIME box|year=1988|num-b=5|num-a=7}}
 +
{{MAA Notice}}

Latest revision as of 17:49, 8 November 2024

Problem

It is possible to place positive integers into the vacant twenty-one squares of the $5 \times 5$ square shown below so that the numbers in each row and column form arithmetic sequences. Find the number that must occupy the vacant square marked by the asterisk (*).

1988 AIME-6.png

Solutions

Solution 1 (specific)

Let the coordinates of the square at the bottom left be $(0,0)$, the square to the right $(1,0)$, etc.

Label the leftmost column (from bottom to top) $0, a, 2a, 3a, 4a$ and the bottom-most row (from left to right) $0, b, 2b, 3b, 4b$. Our method will be to use the given numbers to set up equations to solve for $a$ and $b$, and then calculate $(*)$.

$\begin{tabular}[b]{|c|c|c|c|c|}\hline 4a & & & * & \\ \hline 3a & 74 & & & \\ \hline 2a & & & & 186 \\ \hline a & & 103 & & \\ \hline 0 & b & 2b & 3b & 4b \\ \hline \end{tabular}$

We can compute the squares at the intersections of two existing numbers in terms of $a$ and $b$; two such equations will give us the values of $a$ and $b$. On the fourth row from the bottom, the common difference is $74 - 3a$, so the square at $(2,3)$ has a value of $148 - 3a$. On the third column from the left, the common difference is $103 - 2b$, so that square also has a value of $2b + 3(103 - 2b) = 309 - 4b$. Equating, we get $148 - 3a = 309 - 4b \Longrightarrow 4b - 3a = 161$.

Now we compute the square $(2,2)$. By rows, this value is simply the average of $2a$ and $186$, so it is equal to $\frac{2a + 186}{2} = a + 93$. By columns, the common difference is $103 - 2b$, so our value is $206 - 2b$. Equating, $a + 93 = 206 - 2b \Longrightarrow a + 2b = 113$.

Solving \begin{align*}4b - 3a &= 161\\ a + 2b &= 113 \end{align*}

gives $a = 13$, $b = 50$. Now it is simple to calculate $(4,3)$. One way to do it is to see that $(2,2)$ has $206 - 2b = 106$ and $(4,2)$ has $186$, so $(3,2)$ has $\frac{106 + 186}{2} = 146$. Now, $(3,0)$ has $3b = 150$, so $(3,2) = \frac{(3,0) + (3,4)}{2} \Longrightarrow (3,4) = * = \boxed{142}$.

Solution 2 (general)

First, let $a =$ the number to be placed in the first column, fourth row. Let $b =$ the number to be placed in the second column, fifth row. We can determine the entire first column and fifth row in terms of $a$ and $b$:

$\begin{tabular}[b]{|c|c|c|c|c|}\hline 4a & & & & \\ \hline 3a & & & & \\ \hline 2a & & & & \\ \hline a & & & & \\ \hline 0 & b & 2b & 3b & 4b \\ \hline \end{tabular}$

Next, let $a + b + c =$ the number to be placed in the second column, fourth row. We can determine the entire second column and fourth row in terms of $a$, $b$, and $c$:

$\begin{tabular}[b]{|c|c|c|c|c|}\hline 4a & 4a + b + 4c & & & \\ \hline 3a & 3a + b + 3c & & & \\ \hline 2a & 2a + b + 2c & & & \\ \hline a & a + b + c & a + 2b + 2c & a + 3b + 3c & a + 4b + 4c \\ \hline 0 & b & 2b & 3b & 4b \\ \hline \end{tabular}$

We have now determined at least two values in each row and column. We can finish the table without introducing any more variables:

$\begin{tabular}[b]{|c|c|c|c|c|}\hline 4a & 4a + b + 4c & 4a + 2b + 8c & 4a + 3b + 12c & 4a + 4b + 16c \\ \hline 3a & 3a + b + 3c & 3a + 2b + 6c & 3a + 3b + 9c & 3a + 4b + 12c \\ \hline 2a & 2a + b + 2c & 2a + 2b + 4c & 2a + 3b + 6c & 2a + 4b + 8c \\ \hline a & a + b + c & a + 2b + 2c & a + 3b + 3c & a + 4b + 4c \\ \hline 0 & b & 2b & 3b & 4b \\ \hline \end{tabular}$

We now have a system of equations.

$3a + b + 3c = 74$

$2a + 4b + 8c = 186$

$a + 2b + 2c = 103$

Solving, we find that $(a,b,c) = (13,50, - 5)$. The number in the square marked by the asterisk is $4a + 3b + 12c = \boxed{142}$

Solution 3 (Only one variable)

We begin with the table that was given to us and add in the following arithmetic progression on the bottom:

$\begin{tabular}[b]{|c|c|c|c|c|}\hline & & & * & \\ \hline & 74 & & & \\ \hline & & & & 186 \\ \hline & & 103 & & \\ \hline 0 & x & 2x & 3x & 4x \\ \hline \end{tabular}$

Since all the rows and columns satisfy an arithmetic progression, we have the following:

$\begin{tabular}[b]{|c|c|c|c|c|}\hline & & 412 - 6x & 392 - 5x & 372 - 4x \\ \hline & 74 & 309 - 4x & 294 - 3x & 279 - 2x \\ \hline & & 206 - 2x & 196 - x & 186 \\ \hline & & 103 & 98 + x & 2x + 93 \\ \hline 0 & x & 2x & 3x & 4x \\ \hline \end{tabular}$

We can solve for $x$ in the 2nd row, namely $324 - 5x = 74$ because the arithmetic progression from left to right has difference $x - 15$. Therefore, we have $x = 50$, and because the desired asterisk is $392 - 5x$, the answer is $392 - 250$ = $\boxed {142}$.

~Arcticturn

See also

1988 AIME (Problems • Answer Key • Resources)
Preceded by
Problem 5 		Followed by
Problem 7
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1988_AIME_Problems/Problem_6&oldid=232078"