Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1988 AIME Problems/Problem 7"

m (→‎See also)
(→‎Solution)
 
(16 intermediate revisions by 9 users not shown)
Line 1: Line 1:
−
{{empty}}
 
−
 
 
== Problem ==
 
== Problem ==
 +
In [[triangle]] <math>ABC</math>, <math>\tan \angle CAB = 22/7</math>, and the [[altitude]] from <math>A</math> divides <math>BC</math> into [[segment]]s of length 3 and 17.  What is the area of triangle <math>ABC</math>?
  
 
== Solution ==
 
== Solution ==
 +
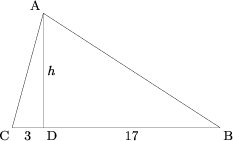
<center>[[Image:AIME_1988_Solution_07.png]]</center>
 +
 +
Call <math>\angle BAD</math> <math>\alpha</math> and <math>\angle CAD</math> <math>\beta</math>. So, <math>\tan \alpha = \frac {17}{h}</math> and <math>\tan \beta = \frac {3}{h}</math>. Using the tangent addition formula <math>\tan (\alpha + \beta) = \dfrac {\tan \alpha + \tan \beta}{1 - \tan \alpha \cdot \tan \beta}</math>, we get <math>\tan (\alpha + \beta) = \dfrac {\frac {20}{h}}{\frac {h^2 - 51}{h^2}} = \frac {22}{7}</math>.
 +
 +
Simplifying, we get <math>\frac {20h}{h^2 - 51} = \frac {22}{7}</math>. Cross-multiplying and simplifying, we get <math>11h^2-70h-561 = 0</math>. Factoring, we get <math>(11h+51)(h-11) = 0</math>, so we take the positive positive solution, which is <math>h = 11</math>. Therefore, the answer is <math>\frac {20 \cdot 11}{2} = 110</math>, so the answer is <math>\boxed {110}</math>.
 +
 +
~Arcticturn
  
 
== See also ==
 
== See also ==
−
* [[1988 AIME Problems]]
+
{{AIME box|year=1988|num-b=6|num-a=8}}
  
−
{{AIME box|year=1988|num-b=6|num-a=8}}
+
[[Category:Intermediate Trigonometry Problems]]
 +
{{MAA Notice}}

Latest revision as of 22:25, 20 November 2023

Problem

In triangle $ABC$, $\tan \angle CAB = 22/7$, and the altitude from $A$ divides $BC$ into segments of length 3 and 17. What is the area of triangle $ABC$?

Solution

AIME 1988 Solution 07.png

Call $\angle BAD$ $\alpha$ and $\angle CAD$ $\beta$. So, $\tan \alpha = \frac {17}{h}$ and $\tan \beta = \frac {3}{h}$. Using the tangent addition formula $\tan (\alpha + \beta) = \dfrac {\tan \alpha + \tan \beta}{1 - \tan \alpha \cdot \tan \beta}$, we get $\tan (\alpha + \beta) = \dfrac {\frac {20}{h}}{\frac {h^2 - 51}{h^2}} = \frac {22}{7}$.

Simplifying, we get $\frac {20h}{h^2 - 51} = \frac {22}{7}$. Cross-multiplying and simplifying, we get $11h^2-70h-561 = 0$. Factoring, we get $(11h+51)(h-11) = 0$, so we take the positive positive solution, which is $h = 11$. Therefore, the answer is $\frac {20 \cdot 11}{2} = 110$, so the answer is $\boxed {110}$.

~Arcticturn

See also

1988 AIME (Problems • Answer Key • Resources)
Preceded by
Problem 6 		Followed by
Problem 8
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1988_AIME_Problems/Problem_7&oldid=204987"