Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2021 AMC 10A Problems/Problem 19"
(→‎Rotation by 45 degrees)
 
(32 intermediate revisions by 15 users not shown)
Line 1: Line 1:
−
We don't know that yet lol
+
==Problem==
 +
The area of the region bounded by the graph of<cmath>x^2+y^2 = 3|x-y| + 3|x+y|</cmath>is <math>m+n\pi</math>, where <math>m</math> and <math>n</math> are integers. What is <math>m + n</math>?
 +
 
 +
<math>\textbf{(A)} ~18\qquad\textbf{(B)} ~27\qquad\textbf{(C)} ~36\qquad\textbf{(D)} ~45\qquad\textbf{(E)} ~54</math>
 +
 
 +
== Solution 1 ==
 +
In order to attack this problem, we can use casework on the sign of <math>|x-y|</math> and <math>|x+y|</math>.
 +
 
 +
Case 1: <math>|x-y|=x-y, |x+y|=x+y</math>
 +
 
 +
Substituting and simplifying, we have <math>x^2-6x+y^2=0</math>, i.e. <math>(x-3)^2+y^2=3^2</math>, which gives us a circle of radius <math>3</math> centered at <math>(3,0)</math>.
 +
 
 +
Case 2: <math>|x-y|=y-x, |x+y|=x+y</math>
 +
 
 +
Substituting and simplifying again, we have <math>x^2+y^2-6y=0</math>, i.e. <math>x^2+(y-3)^2=3^2</math>. This gives us a circle of radius <math>3</math> centered at <math>(0,3)</math>.
 +
 
 +
Case 3: <math>|x-y|=x-y, |x+y|=-x-y</math>
 +
 
 +
Doing the same process as before, we have <math>x^2+y^2+6y=0</math>, i.e. <math>x^2+(y+3)^2=3^2</math>. This gives us a circle of radius <math>3</math> centered at <math>(0,-3)</math>.
 +
 
 +
Case 4: <math>|x-y|=y-x, |x+y|=-x-y</math>
 +
 
 +
One last time: we have <math>x^2+y^2+6x=0</math>, i.e. <math>(x+3)^2+y^2=3^2</math>. This gives us a circle of radius <math>3</math> centered at <math>(-3,0)</math>.
 +
 
 +
After combining all the cases and drawing them on the Cartesian Plane, this is what the diagram looks like:
 +
 
 +
<asy>
 +
size(10cm);
 +
Label f;
 +
f.p=fontsize(7);
 +
xaxis(-8,8,Ticks(f, 1.0));
 +
yaxis(-8,8,Ticks(f, 1.0));
 +
draw(arc((-3,0),3,90,270) -- cycle, gray);
 +
draw(arc((0,3),3,0,180) -- cycle, gray);
 +
draw(arc((3,0),3,-90,90) -- cycle, gray);
 +
draw(arc((0,-3),3,-180,0) -- cycle, gray);
 +
draw((-3,3)--(3,3)--(3,-3)--(-3,-3)--cycle, grey);
 +
</asy>
 +
Now, the area of the shaded region is just a square with side length <math>6</math> with four semicircles of radius <math>3</math>.
 +
The area is <math>6\cdot6+4\cdot \frac{9\pi}{2} = 36+18\pi</math>. The answer is <math>36+18</math> which is <math>\boxed{\textbf{(E) }54}</math>
 +
 
 +
~Bryguy
 +
 
 +
==Solution 2 ==
 +
A somewhat faster variant of solution 1 is to use a bit of symmetry in order to show that the remaining three cases are identical to Case 1 in the above solution, up to rotations by <math>90^{\circ}</math> about the origin. This allows us to quickly sketch the region after solving Case 1.
 +
 
 +
Upon simplifying Case 1, we obtain <math>(x-3)^2 + y^2 = 3^2</math> which is a circle of radius 3 centered at <math>(3,0)</math>. We remark that only the points on the semicircle where <math>x \ge 3</math> work here, since Case 1 assumes <math>x-y \ge 0</math> and <math>x+y \ge 0</math>. Next, we observe that an ordered pair is a solution to the given equation if and only if any of its <math>90^{\circ}</math> rotations about the origin is a solution. This follows as the value of <math>x^2+y^2-3(|x-y|+|x+y|)</math> is invariant to <math>90^{\circ}</math> rotations, since <math>x^2+y^2</math> simply represents the square of the distance to the origin (which is unchanged upon rotation), and <math>|x-y|+|x+y|</math> is the sum of the distances to the lines <math>y=x</math> and <math>y=-x</math>, multiplied by <math>\sqrt{2}</math> (also unchanged upon <math>90^{\circ}</math> rotation).
 +
 
 +
By the above observation, we can quickly sketch the remainder of the region, and the area is <math>\boxed{\textbf{(E) }54}</math> as above.
 +
 
 +
~scrabbler94
 +
 
 +
==Solution 3 (Guessing)==
 +
Assume <math>y</math> = <math>0</math>. We get that <math>x</math> = <math>6</math>. That means that this figure must contain the points <math>(0,6), (6,0), (0, -6), (-6, 0)</math>. Now, assume that <math>x</math> = <math>y</math>. We get that <math>x</math> = <math>3 \sqrt 3</math>. We get the points <math>(3,3), (3,-3), (-3, 3), (-3, -3)</math>.
 +
 
 +
Since this contains <math>x^2 + y^2</math>, assume that there are circles. Therefore, we can guess that there is a center square with area <math>6 \cdot 6</math> = <math>36</math> and <math>4</math> semicircles with radius <math>3</math>. We get <math>4</math> semicircles with area <math>4.5 \pi</math>, and therefore the answer is <math>36+18</math> = <math>\boxed {(E)54}</math>
 +
 
 +
~Arcticturn
 +
 
 +
== Remark ==
 +
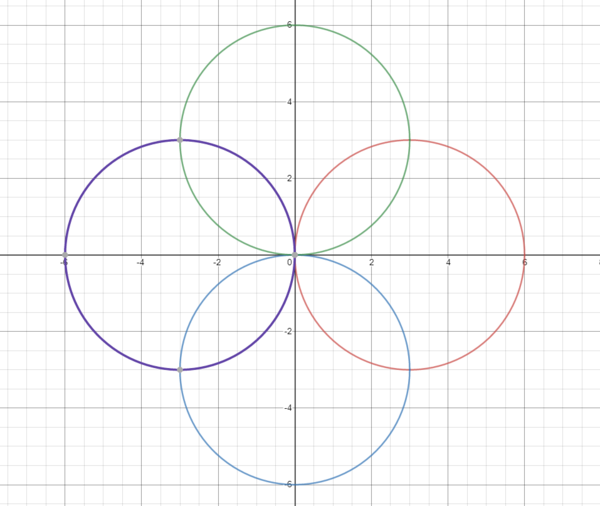
This problem asks for the area of <b>the union of these four circles</b>:
 +
 
 +
[[File:Image 2021-02-11 111327.png|center|600px]]
 +
[[File:Screenshot 2023-06-14 194749]]
 +
 
 +
== Rotation by 45 degrees ==
 +
 
 +
with the help of rotation https://www.wolframalpha.com/input/?i=rotate+45+degrees, we can simplify the equation to <math>a^2 + b^2 = 3\sqrt2|a| + 3\sqrt2|b|</math>. Then follow the previous question
 +
https://artofproblemsolving.com/wiki/index.php/2016_AMC_10B_Problems/Problem_21
 +
 
 +
~aliciawu
 +
 
 +
== Video Solution by OmegaLearn (Using Absolute Value Properties to Graph) ==
 +
https://youtu.be/EHHpB6GIGPc
 +
 
 +
~ pi_is_3.14
 +
 
 +
== Video Solution by The Power Of Logic (Graphing) ==
 +
https://youtu.be/-pa72wBA85Y
 +
 
 +
==Video Solution by TheBeautyofMath==
 +
https://youtu.be/U6obY_kio0g
 +
 
 +
~IceMatrix
 +
 
 +
==See Also==
 +
{{AMC10 box|year=2021|ab=A|num-b=18|num-a=20}}
 +
{{MAA Notice}}

Latest revision as of 19:05, 29 October 2023

Problem

The area of the region bounded by the graph of\[x^2+y^2 = 3|x-y| + 3|x+y|\]is $m+n\pi$, where $m$ and $n$ are integers. What is $m + n$?

$\textbf{(A)} ~18\qquad\textbf{(B)} ~27\qquad\textbf{(C)} ~36\qquad\textbf{(D)} ~45\qquad\textbf{(E)} ~54$

Solution 1

In order to attack this problem, we can use casework on the sign of $|x-y|$ and $|x+y|$.

Case 1: $|x-y|=x-y, |x+y|=x+y$

Substituting and simplifying, we have $x^2-6x+y^2=0$, i.e. $(x-3)^2+y^2=3^2$, which gives us a circle of radius $3$ centered at $(3,0)$.

Case 2: $|x-y|=y-x, |x+y|=x+y$

Substituting and simplifying again, we have $x^2+y^2-6y=0$, i.e. $x^2+(y-3)^2=3^2$. This gives us a circle of radius $3$ centered at $(0,3)$.

Case 3: $|x-y|=x-y, |x+y|=-x-y$

Doing the same process as before, we have $x^2+y^2+6y=0$, i.e. $x^2+(y+3)^2=3^2$. This gives us a circle of radius $3$ centered at $(0,-3)$.

Case 4: $|x-y|=y-x, |x+y|=-x-y$

One last time: we have $x^2+y^2+6x=0$, i.e. $(x+3)^2+y^2=3^2$. This gives us a circle of radius $3$ centered at $(-3,0)$.

After combining all the cases and drawing them on the Cartesian Plane, this is what the diagram looks like:

[asy] size(10cm); Label f; f.p=fontsize(7); xaxis(-8,8,Ticks(f, 1.0)); yaxis(-8,8,Ticks(f, 1.0)); draw(arc((-3,0),3,90,270) -- cycle, gray); draw(arc((0,3),3,0,180) -- cycle, gray); draw(arc((3,0),3,-90,90) -- cycle, gray); draw(arc((0,-3),3,-180,0) -- cycle, gray); draw((-3,3)--(3,3)--(3,-3)--(-3,-3)--cycle, grey); [/asy] Now, the area of the shaded region is just a square with side length $6$ with four semicircles of radius $3$. The area is $6\cdot6+4\cdot \frac{9\pi}{2} = 36+18\pi$. The answer is $36+18$ which is $\boxed{\textbf{(E) }54}$

~Bryguy

Solution 2

A somewhat faster variant of solution 1 is to use a bit of symmetry in order to show that the remaining three cases are identical to Case 1 in the above solution, up to rotations by $90^{\circ}$ about the origin. This allows us to quickly sketch the region after solving Case 1.

Upon simplifying Case 1, we obtain $(x-3)^2 + y^2 = 3^2$ which is a circle of radius 3 centered at $(3,0)$. We remark that only the points on the semicircle where $x \ge 3$ work here, since Case 1 assumes $x-y \ge 0$ and $x+y \ge 0$. Next, we observe that an ordered pair is a solution to the given equation if and only if any of its $90^{\circ}$ rotations about the origin is a solution. This follows as the value of $x^2+y^2-3(|x-y|+|x+y|)$ is invariant to $90^{\circ}$ rotations, since $x^2+y^2$ simply represents the square of the distance to the origin (which is unchanged upon rotation), and $|x-y|+|x+y|$ is the sum of the distances to the lines $y=x$ and $y=-x$, multiplied by $\sqrt{2}$ (also unchanged upon $90^{\circ}$ rotation).

By the above observation, we can quickly sketch the remainder of the region, and the area is $\boxed{\textbf{(E) }54}$ as above.

~scrabbler94

Solution 3 (Guessing)

Assume $y$ = $0$. We get that $x$ = $6$. That means that this figure must contain the points $(0,6), (6,0), (0, -6), (-6, 0)$. Now, assume that $x$ = $y$. We get that $x$ = $3 \sqrt 3$. We get the points $(3,3), (3,-3), (-3, 3), (-3, -3)$.

Since this contains $x^2 + y^2$, assume that there are circles. Therefore, we can guess that there is a center square with area $6 \cdot 6$ = $36$ and $4$ semicircles with radius $3$. We get $4$ semicircles with area $4.5 \pi$, and therefore the answer is $36+18$ = $\boxed {(E)54}$

~Arcticturn

Remark

This problem asks for the area of the union of these four circles:

Image 2021-02-11 111327.png

File:Screenshot 2023-06-14 194749

Rotation by 45 degrees

with the help of rotation https://www.wolframalpha.com/input/?i=rotate+45+degrees, we can simplify the equation to $a^2 + b^2 = 3\sqrt2|a| + 3\sqrt2|b|$. Then follow the previous question https://artofproblemsolving.com/wiki/index.php/2016_AMC_10B_Problems/Problem_21

~aliciawu

Video Solution by OmegaLearn (Using Absolute Value Properties to Graph)

https://youtu.be/EHHpB6GIGPc

~ pi_is_3.14

Video Solution by The Power Of Logic (Graphing)

https://youtu.be/-pa72wBA85Y

Video Solution by TheBeautyofMath

https://youtu.be/U6obY_kio0g

~IceMatrix

See Also

2021 AMC 10A (Problems • Answer Key • Resources)
Preceded by
Problem 18 		Followed by
Problem 20
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2021_AMC_10A_Problems/Problem_19&oldid=200503"