Difference between revisions of "2021 JMPSC Invitationals Problems/Problem 2"
(→Solution) |
Mathdreams (talk | contribs) m |
||
| (4 intermediate revisions by 3 users not shown) | |||
| Line 3: | Line 3: | ||
==Solution== | ==Solution== | ||
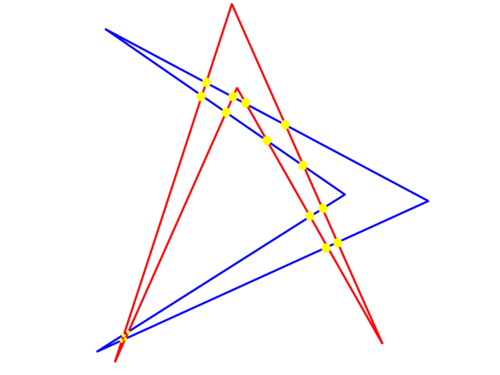
| − | We find that it is possible to construct the maximal <math>\boxed{16}</math> points, where each side of one | + | We find that it is possible to construct the maximal <math>\boxed{16}</math> points, where each side of one quadrilateral intersects all four sides of the other quadrilateral. |
<center> | <center> | ||
| − | [[File: | + | [[File:Invites2D.png|500px]] |
</center> | </center> | ||
~samrocksnature | ~samrocksnature | ||
| + | ==Solution 2== | ||
| + | Take two concave quadrilaterals. Call two lines "somewhat parallel" if the different in their slopes is less than <math>\frac{1}{2}</math>. An arrow has approximately <math>4</math> lines which are "somewhat" parallel, which means <math>2</math> arrows that are <math>90^o</math> to each other form <math>4 \cdot 4 = \boxed{16}</math> intersections. | ||
| + | <math>\linebreak</math> | ||
| + | ~Geometry285 | ||
| + | |||
| + | == Solution 3 == | ||
| + | |||
| + | A line can intersect <math>4</math> other non-parallel lines <math>4</math> times. If we draw <math>2</math> quadrilaterals with non-parallel sides, it would then be possible to get <math>4 \cdot 4 = \boxed{16}</math> intersections. | ||
| + | |||
| + | ~Mathdreams | ||
==See also== | ==See also== | ||
Latest revision as of 11:45, 12 July 2021
Problem
Two quadrilaterals are drawn on the plane such that they share no sides. What is the maximum possible number of intersections of the boundaries of the two quadrilaterals?
Solution
We find that it is possible to construct the maximal 
points, where each side of one quadrilateral intersects all four sides of the other quadrilateral.
~samrocksnature
Solution 2
Take two concave quadrilaterals. Call two lines "somewhat parallel" if the different in their slopes is less than 
. An arrow has approximately 
lines which are "somewhat" parallel, which means 
arrows that are 
to each other form 
intersections.
~Geometry285
Solution 3
A line can intersect other non-parallel lines times. If we draw quadrilaterals with non-parallel sides, it would then be possible to get intersections.
~Mathdreams
See also
- Other 2021 JMPSC Invitationals Problems
- 2021 JMPSC Invitationals Answer Key
- All JMPSC Problems and Solutions
The problems on this page are copyrighted by the Junior Mathematicians' Problem Solving Competition. 
