Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1994 AIME Problems/Problem 2"

(Added Image)
(→‎Solution)
 
(9 intermediate revisions by 8 users not shown)
Line 1: Line 1:
 
== Problem ==
 
== Problem ==
−
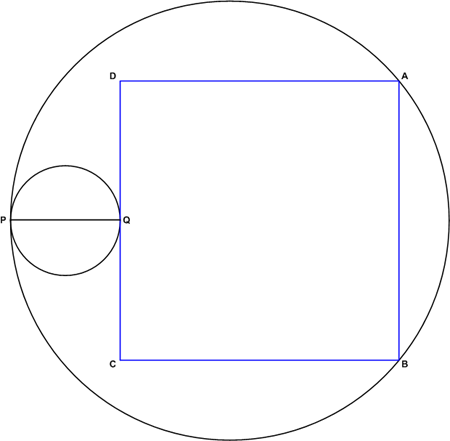
A circle with diameter <math>\overline{PQ}\,</math> of length 10 is internally tangent at <math>P^{}_{}</math> to a circle of radius 20. Square <math>ABCD\,</math> is constructed with <math>A\,</math> and <math>B\,</math> on the larger circle, <math>\overline{CD}\,</math> tangent at <math>Q\,</math> to the smaller circle, and the smaller circle outside <math>ABCD\,</math>. The length of <math>\overline{AB}\,</math> can be written in the form <math>m + \sqrt{n}\,</math>, where <math>m\,</math> and <math>n\,</math> are integers. Find <math>m + n\,</math>.
+
A circle with diameter <math>\overline{PQ}</math> of length 10 is internally tangent at <math>P</math> to a circle of radius 20. Square <math>ABCD</math> is constructed with <math>A</math> and <math>B</math> on the larger circle, <math>\overline{CD}</math> tangent at <math>Q</math> to the smaller circle, and the smaller circle outside <math>ABCD</math>. The length of <math>\overline{AB}</math> can be written in the form <math>m + \sqrt{n}</math>, where <math>m</math> and <math>n</math> are integers. Find <math>m + n</math>.
  
 
[[Image:1994 AIME Problem 2.png]]
 
[[Image:1994 AIME Problem 2.png]]
 +
 +
Note: The diagram was not given during the actual contest.
  
 
== Solution ==
 
== Solution ==
−
Call the center of the larger circle <math>O</math>. Extend the diameter <math>\overline{PQ}</math> to the other side of the square (at point <math>E</math>), and draw <math>\overline{AO}</math>. We now have a [[right triangle]], with [[hypotenuse]] of length <math>20</math>. Since <math>\displaystyle OQ = OP - PQ = 20 - 10 = 10</math>, we know that <math>OE = AB - OQ = AB - 10</math>. The other leg, <math>AE</math>, is just <math>\frac 12 AB</math>.  
+
[[Image:1994 AIME Problem 2 - Solution.png]]
 +
 
 +
Call the center of the larger circle <math>O</math>. Extend the diameter <math>\overline{PQ}</math> to the other side of the square (at point <math>E</math>), and draw <math>\overline{AO}</math>. We now have a [[right triangle]], with [[hypotenuse]] of length <math>20</math>. Since <math>OQ = OP - PQ = 20 - 10 = 10</math>, we know that <math>OE = AB - OQ = AB - 10</math>. The other leg, <math>AE</math>, is just <math>\frac 12 AB</math>.  
  
 
Apply the [[Pythagorean Theorem]]:  
 
Apply the [[Pythagorean Theorem]]:  
  
−
:<math>(AB - 10)^2 + (\frac 12 AB)^2 = 20^2</math>
+
:<math>(AB - 10)^2 + \left(\frac 12 AB\right)^2 = 20^2</math>
 
:<math>AB^2 - 20 AB + 100 + \frac 14 AB^2 - 400 = 0</math>
 
:<math>AB^2 - 20 AB + 100 + \frac 14 AB^2 - 400 = 0</math>
−
:<math>\displaystyle AB^2 - 16 AB - 240 = 0</math>
+
:<math>AB^2 - 16 AB - 240 = 0</math>
 +
 
 +
The [[quadratic formula]] shows that the answer is <math>\frac{16 \pm \sqrt{16^2 + 4 \cdot 240}}{2} = 8 \pm \sqrt{304}</math>. Discard the negative root, so our answer is <math>8 + 304 = \boxed{312}</math>.
  
−
The [[quadratic formula]] shows that the answer is <math>\frac{16 \pm \sqrt{16^2 + 4 \cdot 240}}{2} = 8 \pm \sqrt{304}</math>. Discard the negative root, so our answer is <math>8 + 304 = 312</math>.
+
== Video Solution by OmegaLearn ==
 +
https://youtu.be/nPVDavMoG9M?t=32
  
 +
~ pi_is_3.14
  
 
== See also ==
 
== See also ==
Line 20: Line 28:
  
 
[[Category:Intermediate Geometry Problems]]
 
[[Category:Intermediate Geometry Problems]]
 +
{{MAA Notice}}

Latest revision as of 02:53, 23 January 2023

Problem

A circle with diameter $\overline{PQ}$ of length 10 is internally tangent at $P$ to a circle of radius 20. Square $ABCD$ is constructed with $A$ and $B$ on the larger circle, $\overline{CD}$ tangent at $Q$ to the smaller circle, and the smaller circle outside $ABCD$. The length of $\overline{AB}$ can be written in the form $m + \sqrt{n}$, where $m$ and $n$ are integers. Find $m + n$.

1994 AIME Problem 2.png

Note: The diagram was not given during the actual contest.

Solution

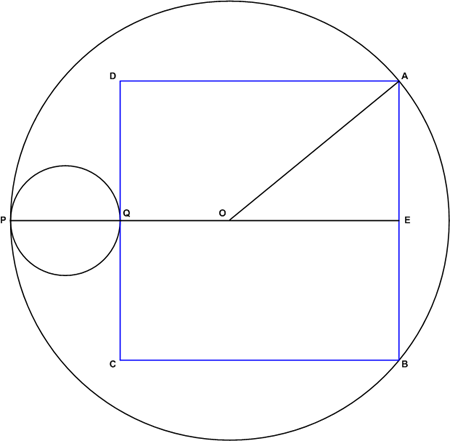
1994 AIME Problem 2 - Solution.png

Call the center of the larger circle $O$. Extend the diameter $\overline{PQ}$ to the other side of the square (at point $E$), and draw $\overline{AO}$. We now have a right triangle, with hypotenuse of length $20$. Since $OQ = OP - PQ = 20 - 10 = 10$, we know that $OE = AB - OQ = AB - 10$. The other leg, $AE$, is just $\frac 12 AB$.

Apply the Pythagorean Theorem:

$(AB - 10)^2 + \left(\frac 12 AB\right)^2 = 20^2$
$AB^2 - 20 AB + 100 + \frac 14 AB^2 - 400 = 0$
$AB^2 - 16 AB - 240 = 0$

The quadratic formula shows that the answer is $\frac{16 \pm \sqrt{16^2 + 4 \cdot 240}}{2} = 8 \pm \sqrt{304}$. Discard the negative root, so our answer is $8 + 304 = \boxed{312}$.

Video Solution by OmegaLearn

https://youtu.be/nPVDavMoG9M?t=32

~ pi_is_3.14

See also

1994 AIME (Problems • Answer Key • Resources)
Preceded by
Problem 1 		Followed by
Problem 3
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1994_AIME_Problems/Problem_2&oldid=187348"