Difference between revisions of "2021 Fall AMC 12A Problems/Problem 13"

Latest revision as of 13:27, 1 September 2024

1 Problem
2 Diagram
3 Solution 1 (Angle Bisector Theorem)
4 Solution 2 (Analytic and Plane Geometry)
5 Solution 3 (Analytic and Plane Geometry)
6 Solution 4 (Distance Between a Point and a Line)
7 Solution 5 (Trigonometry)
8 Solution 6 (Trigonometry)
9 Solution 7 (Vectors)
10 Solution 8 (Dot Product)
11 Video Solution by TheBeautyofMath
12 See Also

Problem

The angle bisector of the acute angle formed at the origin by the graphs of the lines $y = x$ and $y=3x$ has equation $y=kx.$ What is $k?$

$\textbf{(A)} \ \frac{1+\sqrt{5}}{2} \qquad \textbf{(B)} \ \frac{1+\sqrt{7}}{2} \qquad \textbf{(C)} \ \frac{2+\sqrt{3}}{2} \qquad \textbf{(D)} \ 2\qquad \textbf{(E)} \ \frac{2+\sqrt{5}}{2}$

Diagram

$[asy] /* Made by MRENTHUSIASM */ size(250); real xMin = -1; real xMax = 4; real yMin = -1; real yMax = 4; real k = (1+sqrt(5))/2; pair O; O = origin; draw(anglemark(dir((1,1)),O,dir((1,k)),20), red); draw(anglemark(dir((1,k)),O,dir((1,3)),20), red); add(pathticks(anglemark(dir((1,1)),O,dir((1,k)),20), n = 1, r = 0.05, s = 5, red)); add(pathticks(anglemark(dir((1,k)),O,dir((1,3)),20), n = 1, r = 0.05, s = 5, red)); draw((xMin,0)--(xMax,0),black+linewidth(1.5),EndArrow(5)); draw((0,yMin)--(0,yMax),black+linewidth(1.5),EndArrow(5)); label("$x$",(xMax,0),(2,0)); label("$y$",(0,yMax),(0,2)); label("$y=x$",4*dir((1,1))); label("$y=3x$",4*dir((1,3))); label("$y=kx$",4*dir((1,k))); draw(O--3.75*dir((1,1))^^O--3.75*dir((1,3))^^O--3.75*dir((1,k))); [/asy]$ ~MRENTHUSIASM

Solution 1 (Angle Bisector Theorem)

This solution refers to the Diagram section.

Let $O=(0,0), A=(3,3), B=(1,3),$ and $C=\left(\frac3k,3\right).$ As shown below, note that $\overline{OA}, \overline{OB},$ and $\overline{OC}$ are on the lines $y=x, y=3x,$ and $y=kx,$ respectively. By the Distance Formula, we have $OA=3\sqrt2, OB=\sqrt{10}, AC=3-\frac3k,$ and $BC=\frac3k-1.$ $[asy] /* Made by MRENTHUSIASM */ size(250); real xMin = -1; real xMax = 4; real yMin = -1; real yMax = 4; real k = (1+sqrt(5))/2; pair O, A, B, C; O = origin; A = (3,3); B = (1,3); C = (3/k,3); draw(anglemark(dir((1,1)),O,dir((1,k)),20), red); draw(anglemark(dir((1,k)),O,dir((1,3)),20), red); dot("$O$",O,1.5*SW,linewidth(4.5)); dot("$A$",A,1.5*N,linewidth(4.5)); dot("$B$",B,1.5*N,linewidth(4.5)); dot("$C$",C,1.5*N,linewidth(4.5)); add(pathticks(anglemark(dir((1,1)),O,dir((1,k)),20), n = 1, r = 0.05, s = 5, red)); add(pathticks(anglemark(dir((1,k)),O,dir((1,3)),20), n = 1, r = 0.05, s = 5, red)); draw((xMin,0)--(xMax,0),black+linewidth(1.5),EndArrow(5)); draw((0,yMin)--(0,yMax),black+linewidth(1.5),EndArrow(5)); draw(A--B--O--cycle^^O--C); label("$x$",(xMax,0),(2,0)); label("$y$",(0,yMax),(0,2)); label("$3\sqrt{2}$",midpoint(O--A),1.5*E,red+fontsize(10)); label("$\sqrt{10}$",midpoint(O--B),W,red+fontsize(10)); label("$3-\frac3k$",midpoint(A--C),N,red+fontsize(10)); label("$\frac3k-1$",midpoint(B--C),N,red+fontsize(10)); [/asy]$ By the Angle Bisector Theorem, we get $\frac{OA}{OB}=\frac{AC}{BC},$ or $\begin{align*} \frac{3\sqrt2}{\sqrt{10}}&=\frac{3-\frac3k}{\frac3k-1} \\ \frac{3\sqrt2}{\sqrt{10}}&=\frac{3k-3}{3-k} \\ \frac{\sqrt2}{\sqrt{10}}&=\frac{k-1}{3-k} \\ \frac15&=\frac{(k-1)^2}{(3-k)^2} \\ 5(k-1)^2&=(3-k)^2 \\ 4k^2-4k-4&=0 \\ k^2-k-1&=0 \\ k&=\frac{1\pm\sqrt5}{2}. \end{align*}$ Since $k>0,$ the answer is $k=\boxed{\textbf{(A)} \ \frac{1+\sqrt{5}}{2}}.$

Remark

The value of $k$ is known as the Golden Ratio: $\phi=\frac{1+\sqrt{5}}{2}\approx 1.61803398875.$

~MRENTHUSIASM

Solution 2 (Analytic and Plane Geometry)

$[asy] size(180); real xMin = -0.5; real xMax = 2; real yMin = -0.5; real yMax = 4.5; real k = (1+sqrt(5))/2; real m = sqrt(2); real n = sqrt(10); real q = sqrt((5+sqrt(5))/2); pair O; O = origin; draw((xMin,0)--(xMax,0),black+linewidth(1.5),EndArrow(5)); draw((0,yMin)--(0,yMax),black+linewidth(1.5),EndArrow(5)); label("$O$",(-0.2,-0.2),(0,0)); label("$x$",(xMax,0),(2,0)); label("$y$",(0,yMax),(0,2)); label("$A$",(1,0.95),(1,1)); label("$B$",(1,2.80),(1,3)); label("$C$",(1.06,k-0.05),(1,k)); draw(O--m*dir((1,1))^^O--n*dir((1,3))^^O--q*dir((1,k))); draw((1,1)--(1,3)); [/asy]$ Consider the graphs of $f(x)=x$ and $g(x)=3x$ . Since it will be easier to consider at unity, let $x=1$ , then we have $f(1)=1$ and $g(1)=3$ .

Now, let $O$ be $(0,0)$ , $A$ be $(1,1)$ , and $B$ be $(1,3)$ . Cutting through side $AB$ of triangle $OAB$ is the angle bisector $OC$ where $C$ is on side $AB$ .

Hence, by the Angle Bisector Theorem, we get $\frac{OB}{OA}=\frac{BC}{AC}$ .

By the Pythagorean Theorem, $OA=\sqrt{2}$ and $OB=\sqrt{10}$ . Therefore, $\frac{BC}{AC}=\sqrt{5} \implies BC=\sqrt{5}AC$ .

Since $AB=AC+BC=2$ , it is easy derive $AC+\sqrt{5}AC=2 \implies AC=\frac{2}{1+\sqrt{5}}=\frac{-1+\sqrt{5}}{2}$ .

The vertical distance between the $x$ -axis and $C$ is $\frac{-1+\sqrt{5}}{2}+1=\frac{1+\sqrt{5}}{2}$ . Because the $x$ -coordinate of point $C$ is $1$ , the slope we need to find is just the $y$ -coordinate $\boxed{\textbf{(A)} \ \frac{1+\sqrt{5}}{2}}.$

~Wilhelm Z

Solution 3 (Analytic and Plane Geometry)

Let's begin by drawing a triangle that starts at the origin. Assume that the base of the triangle goes to the point $x = 1$ . The line $x = y$ is the hypotenuse of a right triangle with side length $1$ . The hypotenuse' length is $\sqrt 2$ . Then, let's draw the line $x = 3y$ . We extend it to when $x = 1$ . The length of the hypotenuse of the larger triangle is $\sqrt {10}$ with legs $1, 3$ . We then draw the angle bisector. We should label the triangle, so here we go. $AC$ is $1$ . $BC$ is $3$ . $AB$ is $\sqrt {10}$ . When the line with angle $45 ^\circ$ intersects the line $x = 1$ , call the point $D$ . When the angle bisector intersects the line $x = 1$ , call the point $E$ . By Angle Bisector Theorem, $\frac {DE}{DB} = \frac {\sqrt {2}}{\sqrt{10}}$ . Since $BC$ is $3$ and $DC$ is $1$ , we have that $BD$ is $2$ . Solving for $DE$ , we get that $DE$ is $\frac {\sqrt 5 - 1}{2}$ .

Since $DE$ is $\frac {\sqrt 5 - 1}{2}$ , we have that $CE$ is just one more than that. Therefore, $CE$ is $\frac {1+\sqrt 5}{2}$ . Since $AC$ is $1$ , we get that $k$ is $\boxed{\textbf{(A)} \ \frac{1+\sqrt{5}}{2}}$ .

Remark

The answer turns out to be the golden ratio or phi ( $\phi$ ). Phi has many properties and is related to the Fibonacci sequence. See Phi.

~Arcticturn $\blacksquare$

Solution 4 (Distance Between a Point and a Line)

Note that the distance between the point $(m,n)$ to line $Ax + By + C = 0,$ is $\frac{|Am + Bn +C|}{\sqrt{A^2 +B^2}}.$ Because line $y=kx$ is a perpendicular bisector, a point on the line $y=kx$ must be equidistant from the two lines( $y=x$ and $y=3x$ ), call this point $P(z,w).$ Because, the line $y=kx$ passes through the origin, our requested value of $k,$ which is the slope of the angle bisector line, can be found when evaluating the value of $\frac{w}{z}.$ By the Distance from Point to Line formula we get the equation, $\frac{|3z-w|}{\sqrt{10}} = \frac{|z-w|}{\sqrt{2}}.$ Note that $|3z-w|\ge 0,$ because $y=3x$ is higher than $P$ and $|z-w|\le 0,$ because $y=x$ is lower to $P.$ Thus, we solve the equation, $(3z-w)\sqrt{2} = (w-z)\sqrt{10} \Rightarrow 3z-w = \sqrt{5} \cdot(w-z)\Rightarrow (\sqrt{5} +1)w = (3+\sqrt{5})z.$ Thus, the value of $\frac{w}{z} = \frac{3+\sqrt{5}}{1+\sqrt{5}} = \frac{1+\sqrt{5}}{2}.$ Thus, the answer is $\boxed{\textbf{(A)} \ \frac{1+\sqrt{5}}{2}}.$

(Fun Fact: The value $\frac{1+\sqrt{5}}{2}$ is the golden ratio $\phi.$ )

~NH14

Solution 5 (Trigonometry)

This problem can be trivialized using basic trig identities. Let the angle made by $y=x$ and the $x$ -axis be $\theta_{1}$ and the angle made by $y=3x$ and the $x$ -axis be $\theta_{3}$ . Note that $\tan(\theta_{1})=1$ and $\tan(\theta_{3})=3$ , and this is why we named them as such. Let the angle made by $y=kx$ be denoted as $\theta_{k}$ . Since $y=kx$ bisects the two lines, notice that $\theta_k-\theta_1=\theta_3-\theta_k.$

Now, we can take the tangent and apply the tangent subtraction formula: $\begin{align*} \tan(\theta_k-\theta_1)&=\tan(\theta_3-\theta_k)\\ \frac{\tan(\theta_k)-\tan(\theta_1)}{1+\tan(\theta_k)\tan(\theta_1)}&=\frac{\tan(\theta_3)-\tan(\theta_k)}{1+\tan(\theta_3)\tan(\theta_k)}\\ \frac{k-1}{1+k}&=\frac{3-k}{1+3k}\\ (k-1)(1+3k)&=(1+k)(3-k)\\ 3k^2-2k-1&=-k^2+2k+3\\ 4k^2-4k-4&=0\\ k^2-k-1&=0\\ \implies k&=\frac{1\pm \sqrt{5}}{2} \end{align*}$ Since $y=kx$ is increasing, $k>0$ ; thus, $k=\boxed{\textbf{(A)} \ \frac{1+\sqrt{5}}{2}}.$

~Indiiiigo

Solution 6 (Trigonometry)

Denote by $\alpha_1$ , $\alpha_2$ , $\alpha_3$ the acute angles formed between the $x$ -axis and lines $y = x$ , $y = 3 x$ , $y = k x$ , respectively. Hence, $\tan \alpha_1 = 1$ , $\tan \alpha_2 = 3$ , $\tan \alpha_3 = k$ .

Denote by $\theta$ the acute angle formed by lines $y = x$ and $y = 3 x$ .

Hence, $\begin{align*} \tan \theta & = \tan \left( \alpha_2 - \alpha_1 \right) \\ & = \frac{\tan \alpha_2 - \tan \alpha_1}{1 + \tan \alpha_1 \tan \alpha_2} \\ &= \frac{3 - 1}{1 + 1 \cdot 3} \\ & = \frac{1}{2} . \end{align*}$

Following from the double-angle identity, we have $\tan \theta = \frac{2 \tan \frac{\theta}{2}}{1 - \tan^2 \frac{\theta}{2}} .$

Hence, $\tan \frac{\theta}{2} = - 2 \pm \sqrt{5}$ .

Because $\theta$ is acute, $\frac{\theta}{2}$ is acute. Hence, $\tan \frac{\theta}{2} > 0$ . Hence, $\tan \frac{\theta}{2} = - 2 + \sqrt{5}$ .

Because line $y = kx$ is the angle bisector of $\theta$ , the angle between lines $y = x$ and $y = k x$ is $\frac{\theta}{2}$ .

Hence, $\begin{align*} \tan \alpha_3 & = \tan \left( \alpha_1 + \frac{\theta}{2} \right) \\ & = \frac{\tan \alpha_1 + \tan \frac{\theta}{2}}{1 - \tan \alpha_1 \tan \frac{\theta}{2}} \\ &= \frac{1 + \left( - 2 + \sqrt{5} \right)}{1 - 1 \cdot \left( - 2 + \sqrt{5} \right) } \\ & = \frac{\sqrt{5} - 1}{3 - \sqrt{5}} \\ & = \frac{1 + \sqrt{5}}{2} . \end{align*}$

Therefore, the answer is $\boxed{\textbf{(A) }\frac{1 + \sqrt{5}}{2}}$ .

~Steven Chen (www.professorchenedu.com)

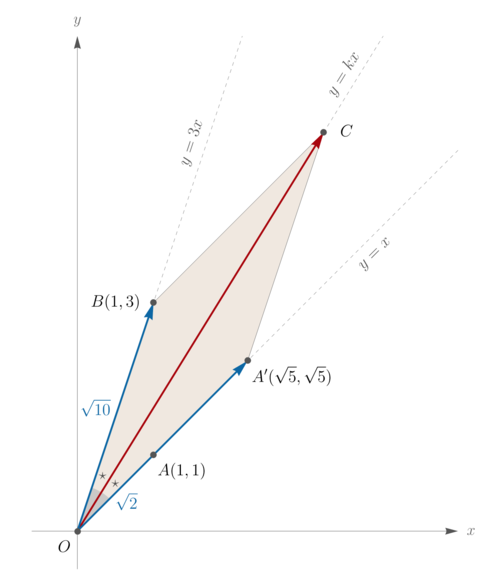
Solution 7 (Vectors)

When drawing the lines $y=x$ and $y=3x$ , it is natural to choose points $A(1,1)$ and $B(1,3)$ together with origin $O$ . See the figure attached. We utilize the fact that if $\mathbf{u}$ and $\mathbf{v}$ are vectors of same length, then $\mathbf{u} + \mathbf{v}$ bisects the angle between $\mathbf{u}$ and $\mathbf{v}$ .

In particular, we scale the vector $\overrightarrow{OA} = (1,1)$ by the factor of $\frac{OB}{OA} = \frac{\sqrt{10}}{\sqrt{2}} = \sqrt{5}$ to get $\overrightarrow{OA'} \coloneqq \sqrt{5}\,\overrightarrow{OA} = \left(\sqrt{5}, \sqrt{5}\right)$ . So by adding vectors $\overrightarrow{OA'}$ and $\overrightarrow{OB} = (1,3)$ we get ${\color[rgb]{0.666667,0,0}\overrightarrow{OC}} \coloneqq {\color[rgb]{0,0.4,0.65}\overrightarrow{OA'}} + {\color[rgb]{0,0.4,0.65}\overrightarrow{OB}} = \left( 1 + \sqrt{5}, 3 + \sqrt{5} \right)$ which bisects the acute angle formed by lines $OA: y = x$ and $OB: y = 3x$ . (In other words, quadrilateral $OBCA'$ is a rhombus.) Finally, observe that $C\!\left(1+\sqrt{5}, 3+\sqrt{5}\right)$ lies on the line $y = kx$ whose slope is $k = \frac{3+\sqrt{5}}{1+\sqrt{5}} = \frac{1+\sqrt{5}}{2}.$ Thus, the answer is $\boxed{\textbf{(A)}\;\frac{1+\sqrt{5}}{2}}$ . $\blacksquare$

~VensL.

Solution 8 (Dot Product)

We notice that the line $y = x$ can be represented as the vector $\vec{A} = \begin{bmatrix} 1 \\ 1 \end{bmatrix}$ and $y = 3x$ as $\vec{B} = \begin{bmatrix} 1 \\ 3 \end{bmatrix}$ as the "slope" of both vectors represent the coefficient of $x$ .

Then, we can represent $y = kx$ as $\vec{C} = \begin{bmatrix} 1 \\ k \end{bmatrix}$ and notice that since $C$ is in essence an angle bisector, $\theta = \angle \vec{A}\vec{C} = \angle \vec{B}\vec{C}$

$A \cdot C = |A|\cdot|C|\cos(\theta_1)$ where $\theta_1 = \angle \vec{A}\vec{C} = \theta$ $B \cdot C = |B|\cdot|C|\cos(\theta_2)$ where $\theta_2 = \angle \vec{B}\vec{C} = \theta$

Since both $\theta_i$ 's are equivalent, we may simply represent them with $\theta$ .

Simplifying both equations by performing the necessary operations, we get

$1+k = \sqrt{2} \cdot \sqrt{k^2 + 1} \cdot \cos(\theta) \implies \frac{1+k}{\sqrt{2}} = \sqrt{k^2 + 1} \cos(\theta)$

$1+3k = \sqrt{10} \cdot \sqrt{k^2 + 1} \cdot \cos(\theta)$

Substituting the first into the second, we get $1 + 3k = \sqrt{10} \cdot \frac{1+k}{\sqrt{2}} \implies k=\boxed{\textbf{(A)} \ \frac{1+\sqrt{5}}{2}}$

~ $\color{magenta} zoomanTV$

Video Solution by TheBeautyofMath

https://youtu.be/ToiOlqWz3LY?t=504

~IceMatrix

2021 Fall AMC 12A (Problems • Answer Key • Resources)
Preceded by Problem 12	Followed by Problem 14
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

Page

Toolbox

Search