Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2016 AIME I Problems/Problem 15"

(→‎Solution 1)
 
(9 intermediate revisions by 6 users not shown)
Line 3: Line 3:
 
Circles <math>\omega_1</math> and <math>\omega_2</math> intersect at points <math>X</math> and <math>Y</math>. Line <math>\ell</math> is tangent to <math>\omega_1</math> and <math>\omega_2</math> at <math>A</math> and <math>B</math>, respectively, with line <math>AB</math> closer to point <math>X</math> than to <math>Y</math>. Circle <math>\omega</math> passes through <math>A</math> and <math>B</math> intersecting <math>\omega_1</math> again at <math>D \neq A</math> and intersecting <math>\omega_2</math> again at <math>C \neq B</math>. The three points <math>C</math>, <math>Y</math>, <math>D</math> are collinear, <math>XC = 67</math>, <math>XY = 47</math>, and <math>XD = 37</math>. Find <math>AB^2</math>.
 
Circles <math>\omega_1</math> and <math>\omega_2</math> intersect at points <math>X</math> and <math>Y</math>. Line <math>\ell</math> is tangent to <math>\omega_1</math> and <math>\omega_2</math> at <math>A</math> and <math>B</math>, respectively, with line <math>AB</math> closer to point <math>X</math> than to <math>Y</math>. Circle <math>\omega</math> passes through <math>A</math> and <math>B</math> intersecting <math>\omega_1</math> again at <math>D \neq A</math> and intersecting <math>\omega_2</math> again at <math>C \neq B</math>. The three points <math>C</math>, <math>Y</math>, <math>D</math> are collinear, <math>XC = 67</math>, <math>XY = 47</math>, and <math>XD = 37</math>. Find <math>AB^2</math>.
  
 +
==Solution==
 +
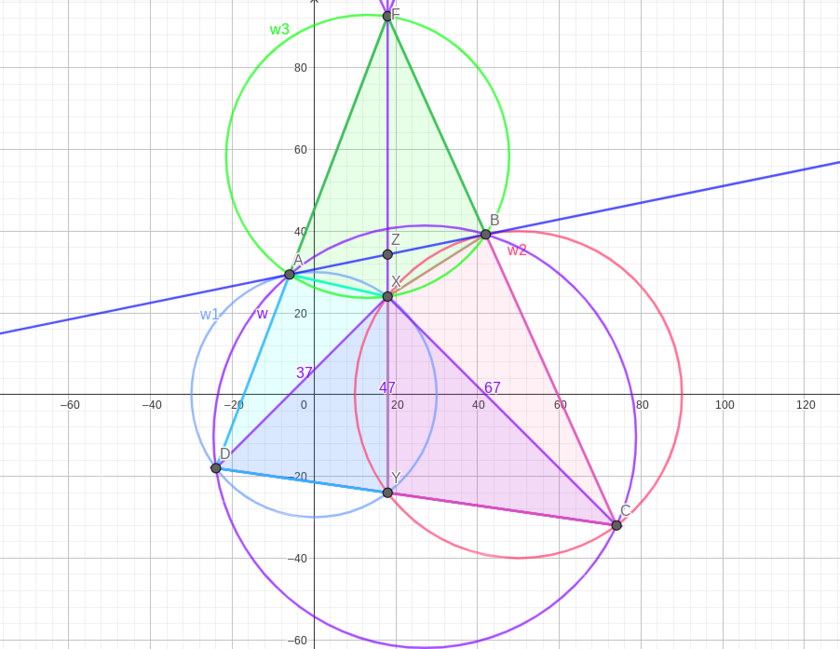
Using the radical axis theorem, the lines <math>\overline{AD}, \overline{BC}, \overline{XY}</math> are all concurrent at one point, call it <math>F</math>. Now recall by Miquel's theorem in <math>\triangle FDC</math> the fact that quadrilaterals <math>DAXY</math> and <math>CBXY</math> are cyclic implies <math>FAXB</math> is cyclic as well. Denote <math>\omega_{3}\equiv(FAXB)</math> and <math>Z\equiv\ell\cap\overline{FXY}</math>.
 +
 +
Since point <math>Z</math> lies on the radical axis of <math>\omega_{1},\omega_{2}</math>, it has equal power with respect to both circles, thus <cmath>AZ^{2}=\text{Pow}_{\omega_{1}}(Z)=ZX\cdot ZY=\text{Pow}_{\omega_{2}}(Z)=ZB^{2}\implies AZ=ZB.</cmath> Also, notice that <cmath>AZ\cdot ZB=\text{Pow}_{\omega_{3}}(Z)=ZX\cdot ZF\implies ZY=ZF.</cmath> The diagonals of quadrilateral <math>FAYB</math> bisect each other at <math>Z</math>, so we conclude that <math>FAYB</math> is a parallelogram. Let <math>u:=ZX</math>, so that <math>ZY=ZF=u+47</math>.
 +
 +
Because <math>FAYB</math> is a parallelogram and quadrilaterals <math>DAXY, CBXY</math> are cyclic, <cmath>\angle DFX=\angle AFX=\angle BYX=\angle BCX=\angle FCX~~\text{and}~~\angle XDF=\angle XDA=\angle XYA=\angle XFB=\angle XFC</cmath> so we have the pair of similar triangles <math>\triangle DFX~\sim~\triangle FCX</math>. Thus <cmath>\dfrac{37}{2u+47}=\dfrac{2u+47}{67}\implies 2u+47=\sqrt{37\cdot 67}\implies u=\dfrac{1}{2}\left(\sqrt{37\cdot 67}-47\right).</cmath> Now compute <cmath>AB^{2}=4AZ^{2}=4\cdot ZX\cdot ZY=4u(u+47)=37\cdot 67-47^{2}=\textbf{270}.</cmath>
 +
 +
[[File:AIME 2016-I15 Geogebra Diagram.png|840px]]
  
 
==Solution 1==
 
==Solution 1==
  
−
Let <math>Z = XY \cap AB</math>. By the radical axis theorem <math>AD, XY, BC</math> are concurrent, say at <math>P</math>. Moreover, <math>\triangle DXP \sim \triangle PXC</math> by simple angle chasing. Let <math>y = PX, x = XY</math>. Then <cmath>\frac{y}{37} = \frac{67}{y} \qquad \implies \qquad y^2 = 37 \cdot 67.</cmath> Now, <math>AZ^2 = \tfrac 14 AB^2</math>, and by power of a point, <cmath>\begin{align*}
+
Let <math>Z = XY \cap AB</math>. By the radical axis theorem <math>AD, XY, BC</math> are concurrent, say at <math>P</math>. Moreover, <math>\triangle DXP \sim \triangle PXC</math> by simple angle chasing. Let <math>y = PX, x = XZ</math>. Then <cmath>\frac{y}{37} = \frac{67}{y} \qquad \implies \qquad y^2 = 37 \cdot 67.</cmath> Now, <math>AZ^2 = \tfrac 14 AB^2</math>, and by power of a point, <cmath>\begin{align*}
 
         x(y-x) &= \tfrac 14 AB^2, \quad \text{and} \\
 
         x(y-x) &= \tfrac 14 AB^2, \quad \text{and} \\
 
         x(47+x) &= \tfrac 14 AB^2
 
         x(47+x) &= \tfrac 14 AB^2
Line 130: Line 138:
  
 
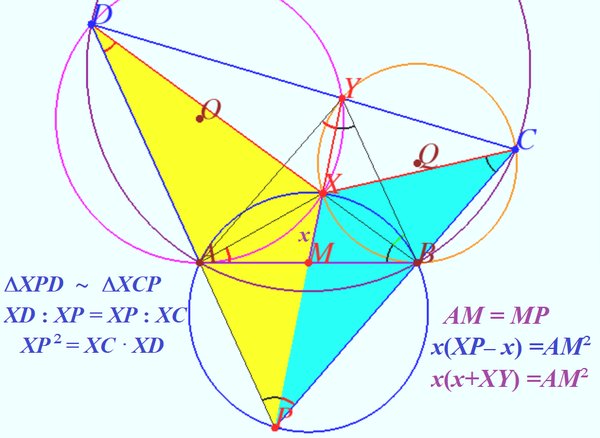
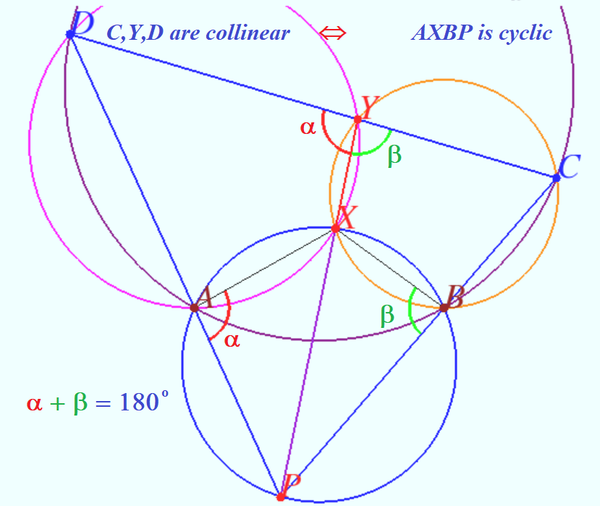
==Solution 6 (No words)==
 
==Solution 6 (No words)==
−
[[File:2016 AIME I 15.png|450px|right]]
+
[[File:2016 AIME I 15.png|600px|right]]
−
[[File:2016 AIME I 15b.png|400px|left]]
+
[[File:2016 AIME I 15b.png|600px|left]]
−
<math> - \\ - </math>
 
  
−
'''Shelomovskii, vvsss,  www.deoma-cmd.ru'''
+
<math>AB^2 = 4 AM^2 =2x(2x+ 2 XY) =(XP - XY) (XP + XY) = XP^2 - XY^2 = XC \cdot XD - XY^2 = 67 \cdot 37 - 47^2 = \boxed{270}.</math>
 +
 
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
 
 +
==Solution 7 (Linearity of Power of a Point)==
 +
Extend <math>\overline{AD}</math> and <math>\overline{BC}</math> to meet at point <math>P</math>. Let <math>M</math> be the midpoint of segment <math>AB</math>. Then by radical axis on <math>(ADY)</math>, <math>(BCY)</math> and <math>(ABCD)</math>, <math>P</math> lies on <math>XY</math>. By the bisector lemma, <math>M</math> lies on <math>XY</math>. It is well-known that <math>P</math>, <math>A</math>, <math>X</math>, and <math>B</math> are concyclic. By Power of a point on <math>M</math> with respect to <math>(PAXB)</math> and <math>(ADY)</math>, <cmath> |\text{Pow}(M, (PAXB))| = MX \cdot MP = MA^2 = |\text{Pow}(M, (ADY))| = MX \cdot MY, </cmath> so <math>MP=MY</math>. Thus <math>AB</math> and <math>PY</math> bisect each other, so <math>PAYB</math> is a parallelogram. This implies that <cmath> \angle DAY = \angle YBC, </cmath> so by the inscribed angle theorem <math>\overline{XY}</math> bisects <math>\angle DXC</math>.
 +
 
 +
Claim: <math>AB^2 = DY \cdot YC</math>.
 +
 
 +
Proof. Define the linear function <math>f(\bullet) := \text{Pow}(\bullet, (ADY)) - \text{Pow}(\bullet, (ABCD))</math>. Since <math>\overline{BY}</math> is parallel to the radical axis <math>\overline{AD}</math> of <math>(ADY)</math> and <math>(ABCD)</math> by our previous parallelism, <math>f(B)=f(Y)</math>. Note that <math>f(B)=AB^2</math> while <math>f(Y)=DY \cdot YC</math>, so we conclude. <math>\square</math>
 +
 
 +
By Stewart's theorem on <math>\triangle DXC</math>, <math>DY \cdot YC=37 \cdot 67 - 47^2 = 270</math>, so <math>AB^2=\boxed{270}</math>.
 +
 
 +
~ Leo.Euler
 +
 
 +
==Video Solution by MOP 2024==
 +
https://youtu.be/qFfgB15fYS8
 +
 
 +
~r00tsOfUnity
  
 
==Video Solution==
 
==Video Solution==
 
https://youtu.be/QoVIorvv_I8
 
https://youtu.be/QoVIorvv_I8
 +
 +
~MathProblemSolvingSkills.com
 +
 +
==Video Solution by The Power of Logic==
 +
https://youtu.be/lTZx6tp2Fvg
  
 
==See Also==
 
==See Also==
 
{{AIME box|year=2016|n=I|num-b=14|after=Last Question}}
 
{{AIME box|year=2016|n=I|num-b=14|after=Last Question}}
 
{{MAA Notice}}
 
{{MAA Notice}}

Latest revision as of 16:12, 8 January 2024

Problem

Circles $\omega_1$ and $\omega_2$ intersect at points $X$ and $Y$. Line $\ell$ is tangent to $\omega_1$ and $\omega_2$ at $A$ and $B$, respectively, with line $AB$ closer to point $X$ than to $Y$. Circle $\omega$ passes through $A$ and $B$ intersecting $\omega_1$ again at $D \neq A$ and intersecting $\omega_2$ again at $C \neq B$. The three points $C$, $Y$, $D$ are collinear, $XC = 67$, $XY = 47$, and $XD = 37$. Find $AB^2$.

Solution

Using the radical axis theorem, the lines $\overline{AD}, \overline{BC}, \overline{XY}$ are all concurrent at one point, call it $F$. Now recall by Miquel's theorem in $\triangle FDC$ the fact that quadrilaterals $DAXY$ and $CBXY$ are cyclic implies $FAXB$ is cyclic as well. Denote $\omega_{3}\equiv(FAXB)$ and $Z\equiv\ell\cap\overline{FXY}$.

Since point $Z$ lies on the radical axis of $\omega_{1},\omega_{2}$, it has equal power with respect to both circles, thus \[AZ^{2}=\text{Pow}_{\omega_{1}}(Z)=ZX\cdot ZY=\text{Pow}_{\omega_{2}}(Z)=ZB^{2}\implies AZ=ZB.\] Also, notice that \[AZ\cdot ZB=\text{Pow}_{\omega_{3}}(Z)=ZX\cdot ZF\implies ZY=ZF.\] The diagonals of quadrilateral $FAYB$ bisect each other at $Z$, so we conclude that $FAYB$ is a parallelogram. Let $u:=ZX$, so that $ZY=ZF=u+47$.

Because $FAYB$ is a parallelogram and quadrilaterals $DAXY, CBXY$ are cyclic, \[\angle DFX=\angle AFX=\angle BYX=\angle BCX=\angle FCX~~\text{and}~~\angle XDF=\angle XDA=\angle XYA=\angle XFB=\angle XFC\] so we have the pair of similar triangles $\triangle DFX~\sim~\triangle FCX$. Thus \[\dfrac{37}{2u+47}=\dfrac{2u+47}{67}\implies 2u+47=\sqrt{37\cdot 67}\implies u=\dfrac{1}{2}\left(\sqrt{37\cdot 67}-47\right).\] Now compute \[AB^{2}=4AZ^{2}=4\cdot ZX\cdot ZY=4u(u+47)=37\cdot 67-47^{2}=\textbf{270}.\]

AIME 2016-I15 Geogebra Diagram.png

Solution 1

Let $Z = XY \cap AB$. By the radical axis theorem $AD, XY, BC$ are concurrent, say at $P$. Moreover, $\triangle DXP \sim \triangle PXC$ by simple angle chasing. Let $y = PX, x = XZ$. Then \[\frac{y}{37} = \frac{67}{y} \qquad \implies \qquad y^2 = 37 \cdot 67.\] Now, $AZ^2 = \tfrac 14 AB^2$, and by power of a point, \begin{align*} x(y-x) &= \tfrac 14 AB^2, \quad \text{and} \\ x(47+x) &= \tfrac 14 AB^2 \end{align*} Solving, we get \[\tfrac 14 AB^2 = \tfrac 12 (y-47)\cdot \tfrac 12 (y+47) \qquad \implies\] \[\qquad AB ^ 2 = 37\cdot 67 - 47^2 = \boxed{270}\]

Solution 2

By the Radical Axis Theorem $AD, XY, BC$ concur at point $E$.

Let $AB$ and $EY$ intersect at $S$. Note that because $AXDY$ and $CYXB$ are cyclic, by Miquel's Theorem $AXBE$ is cyclic as well. Thus \[\angle AEX = \angle ABX = \angle XCB = \angle XYB\]and \[\angle XEB = \angle XAB = \angle XDA = \angle XYA.\]Thus $AY \parallel EB$ and $YB \parallel EA$, so $AEBY$ is a parallelogram. Hence $AS = SB$ and $SE = SY$. But notice that $DXE$ and $EXC$ are similar by $AA$ Similarity, so $XE^2 = XD \cdot XC = 37 \cdot 67$. But \[XE^2 - XY^2 = (XE + XY)(XE - XY) = EY \cdot 2XS = 2SY \cdot 2SX = 4SA^2 = AB^2.\]Hence $AB^2 = 37 \cdot 67 - 47^2 = \boxed{270}.$

Solution 3

First, we note that as $\triangle XDY$ and $\triangle XYC$ have bases along the same line, $\frac{[\triangle XDY]}{[\triangle XYC]}=\frac{DY}{YC}$. We can also find the ratio of their areas using the circumradius area formula. If $R_1$ is the radius of $\omega_1$ and if $R_2$ is the radius of $\omega_2$, then \[\frac{[\triangle XDY]}{[\triangle XYC]}=\frac{(37\cdot 47\cdot DY)/(4R_1)}{(47\cdot 67\cdot YC)/(4R_2)}=\frac{37\cdot DY\cdot R_2}{67\cdot YC\cdot R_1}.\] Since we showed this to be $\frac{DY}{YC}$, we see that $\frac{R_2}{R_1}=\frac{67}{37}$.

We extend $AD$ and $BC$ to meet at point $P$, and we extend $AB$ and $CD$ to meet at point $Q$ as shown below. [asy] size(200); import olympiad; real R1=45,R2=67*R1/37; real m1=sqrt(R1^2-23.5^2); real m2=sqrt(R2^2-23.5^2); pair o1=(0,0),o2=(m1+m2,0),x=(m1,23.5),y=(m1,-23.5); draw(circle(o1,R1)); draw(circle(o2,R2)); pair q=(-R1/(R2-R1)*o2.x,0); pair a=tangent(q,o1,R1,2); pair b=tangent(q,o2,R2,2); pair d=intersectionpoints(circle(o1,R1),q--y+15*(y-q))[0]; pair c=intersectionpoints(circle(o2,R2),q--y+15*(y-q))[1]; pair p=extension(a,d,b,c); dot(q^^a^^b^^x^^y^^c^^d^^p); draw(q--b^^q--c); draw(p--d^^p--c^^x--y); draw(a--y^^b--y); draw(d--x--c); label("$A$",a,NW,fontsize(8)); label("$B$",b,NE,fontsize(8)); label("$C$",c,SE,fontsize(8)); label("$D$",d,SW,fontsize(8)); label("$X$",x,2*WNW,fontsize(8)); label("$Y$",y,3*S,fontsize(8)); label("$P$",p,N,fontsize(8)); label("$Q$",q,W,fontsize(8)); [/asy] As $ABCD$ is cyclic, we know that $\angle BCD=180-\angle DAB=\angle BAP$. But then as $AB$ is tangent to $\omega_2$ at $B$, we see that $\angle BCD=\angle ABY$. Therefore, $\angle ABY=\angle BAP$, and $BY\parallel PD$. A similar argument shows $AY\parallel PC$. These parallel lines show $\triangle PDC\sim\triangle ADY\sim\triangle BYC$. Also, we showed that $\frac{R_2}{R_1}=\frac{67}{37}$, so the ratio of similarity between $\triangle ADY$ and $\triangle BYC$ is $\frac{37}{67}$, or rather \[\frac{AD}{BY}=\frac{DY}{YC}=\frac{YA}{CB}=\frac{37}{67}.\] We can now use the parallel lines to find more similar triangles. As $\triangle AQD\sim \triangle BQY$, we know that \[\frac{QA}{QB}=\frac{QD}{QY}=\frac{AD}{BY}=\frac{37}{67}.\] Setting $QA=37x$, we see that $QB=67x$, hence $AB=30x$, and the problem simplifies to finding $30^2x^2$. Setting $QD=37^2y$, we also see that $QY=37\cdot 67y$, hence $DY=37\cdot 30y$. Also, as $\triangle AQY\sim \triangle BQC$, we find that \[\frac{QY}{QC}=\frac{YA}{CB}=\frac{37}{67}.\] As $QY=37\cdot 67y$, we see that $QC=67^2y$, hence $YC=67\cdot30y$.

Applying Power of a Point to point $Q$ with respect to $\omega_2$, we find \[67^2x^2=37\cdot 67^3 y^2,\] or $x^2=37\cdot 67 y^2$. We wish to find $AB^2=30^2x^2=30^2\cdot 37\cdot 67y^2$.

Applying Stewart's Theorem to $\triangle XDC$, we find \[37^2\cdot (67\cdot 30y)+67^2\cdot(37\cdot 30y)=(67\cdot 30y)\cdot (37\cdot 30y)\cdot (104\cdot 30y)+47^2\cdot (104\cdot 30y).\] We can cancel $30\cdot 104\cdot y$ from both sides, finding $37\cdot 67=30^2\cdot 67\cdot 37y^2+47^2$. Therefore, \[AB^2=30^2\cdot 37\cdot 67y^2=37\cdot 67-47^2=\boxed{270}.\]

Solution 4

[asy] size(9cm); import olympiad; real R1=45,R2=67*R1/37; real m1=sqrt(R1^2-23.5^2); real m2=sqrt(R2^2-23.5^2); pair o1=(0,0),o2=(m1+m2,0),x=(m1,23.5),y=(m1,-23.5); draw(circle(o1,R1)); draw(circle(o2,R2)); pair q=(-R1/(R2-R1)*o2.x,0); pair a=tangent(q,o1,R1,2); pair b=tangent(q,o2,R2,2); pair d=intersectionpoints(circle(o1,R1),q--y+15*(y-q))[0]; pair c=intersectionpoints(circle(o2,R2),q--y+15*(y-q))[1]; dot(a^^b^^x^^y^^c^^d); draw(x--y); draw(a--y^^b--y); draw(d--x--c); draw(a--b--c--d--cycle); draw(x--a^^x--b); label("$A$",a,NW,fontsize(9)); label("$B$",b,NE,fontsize(9)); label("$C$",c,SE,fontsize(9)); label("$D$",d,SW,fontsize(9)); label("$X$",x,2*N,fontsize(9)); label("$Y$",y,3*S,fontsize(9)); [/asy] First of all, since quadrilaterals $ADYX$ and $XYCB$ are cyclic, we can let $\angle DAX = \angle XYC = \theta$, and $\angle XYD = \angle CBX = 180 - \theta$, due to the properties of cyclic quadrilaterals. In addition, let $\angle BAX = x$ and $\angle ABX = y$. Thus, $\angle ADX = \angle AYX = x$ and $\angle XYB = \angle XCB = y$. Then, since quadrilateral $ABCD$ is cyclic as well, we have the following sums: \[\theta + x +\angle XCY + y = 180^{\circ}\] \[180^{\circ} - \theta + y + \angle XDY + x = 180^{\circ}\] Cancelling out $180^{\circ}$ in the second equation and isolating $\theta$ yields $\theta = y + \angle XDY + x$. Substituting $\theta$ back into the first equation, we obtain \[2x + 2y + \angle XCY + \angle XDY = 180^{\circ}\] Since \[x + y +\angle XAY + \angle XCY + \angle DAY = 180^{\circ}\] \[x + y + \angle XDY + \angle XCY + \angle DAY = 180^{\circ}\] we can then imply that $\angle DAY = x + y$. Similarly, $\angle YBC = x + y$. So then $\angle DXY = \angle YXC = x + y$, so since we know that $XY$ bisects $\angle DXC$, we can solve for $DY$ and $YC$ with Stewart’s Theorem. Let $DY = 37n$ and $YC = 67n$. Then \[37n \cdot 67n \cdot 104n + 47^2 \cdot 104n = 37^2 \cdot 67n + 67^2 \cdot 37n\] \[37n \cdot 67n + 47^2 = 37 \cdot 67\] \[n^2 = \frac{270}{2479}\] Now, since $\angle AYX = x$ and $\angle BYX = y$, $\angle AYB = x + y$. From there, let $\angle AYD = \alpha$ and $\angle BYC = \beta$. From angle chasing we can derive that $\angle YDX = \angle YAX = \beta - x$ and $\angle YCX = \angle YBX = \alpha - y$. From there, since $\angle ADX = x$, it is quite clear that $\angle ADY = \beta$, and $\angle YAB = \beta$ can be found similarly. From there, since $\angle ADY = \angle YAB = \angle BYC = \beta$ and $\angle DAY = \angle AYB = \angle YBC = x + y$, we have $AA$ similarity between $\triangle DAY$, $\triangle AYB$, and $\triangle YBC$. Therefore the length of $AY$ is the geometric mean of the lengths of $DA$ and $YB$ (from $\triangle DAY \sim \triangle AYB$). However, $\triangle DAY \sim \triangle AYB \sim \triangle YBC$ yields the proportion $\frac{AD}{DY} = \frac{YA}{AB} = \frac{BY}{YC}$; hence, the length of $AB$ is the geometric mean of the lengths of $DY$ and $YC$. We can now simply use arithmetic to calculate $AB^2$. \[AB^2 = DY \cdot YC\] \[AB^2 = 37 \cdot 67 \cdot \frac{270}{2479}\] \[AB^2 = \boxed{270}\]

-Solution by TheBoomBox77

Solution 5 (not too different)

Let $E = DA \cap CB$. By Radical Axes, $E$ lies on $XY$. Note that $EAXB$ is cyclic as $X$ is the Miquel point of $\triangle EDC$ in this configuration.

Claim. $\triangle DXE \sim \triangle EXC$ Proof. We angle chase. \[\measuredangle XEC = \measuredangle XEB = \measuredangle XAB = \measuredangle XDA = \measuredangle XDE\]and\[\measuredangle XCE = \measuredangle XCB = \measuredangle XBA = \measuredangle XEA = \measuredangle XED. \square\]

Let $F = EX \cap AB$. Note \[FA^2 = FX \cdot FY = FB^2\]and\[EF \cdot FX = AF \cdot FB = FA^2 = FX \cdot FY \implies EF = FY\]By our claim, \[\frac{DX}{XE} = \frac{EX}{XC} \implies EX^2 = DX \cdot XC = 67 \cdot 37 \implies FY = \frac{EY}{2} = \frac{EX+XY}{2} = \frac{\sqrt{67 \cdot 37}+47}{2}\]and\[FX=FY-47=\frac{\sqrt{67 \cdot 37}-47}{2}\]Finally, \[AB^2 = (2 \cdot FA)^2 = 4 \cdot FX \cdot FY = 4 \cdot \frac{(67 \cdot 37) - 47^2}{4} = \boxed{270}. \blacksquare\]~Mathscienceclass


Solution 6 (No words)

2016 AIME I 15.png
2016 AIME I 15b.png

$AB^2 = 4 AM^2 =2x(2x+ 2 XY) =(XP - XY) (XP + XY) = XP^2 - XY^2 = XC \cdot XD - XY^2 = 67 \cdot 37 - 47^2 = \boxed{270}.$

vladimir.shelomovskii@gmail.com, vvsss

Solution 7 (Linearity of Power of a Point)

Extend $\overline{AD}$ and $\overline{BC}$ to meet at point $P$. Let $M$ be the midpoint of segment $AB$. Then by radical axis on $(ADY)$, $(BCY)$ and $(ABCD)$, $P$ lies on $XY$. By the bisector lemma, $M$ lies on $XY$. It is well-known that $P$, $A$, $X$, and $B$ are concyclic. By Power of a point on $M$ with respect to $(PAXB)$ and $(ADY)$, \[|\text{Pow}(M, (PAXB))| = MX \cdot MP = MA^2 = |\text{Pow}(M, (ADY))| = MX \cdot MY,\] so $MP=MY$. Thus $AB$ and $PY$ bisect each other, so $PAYB$ is a parallelogram. This implies that \[\angle DAY = \angle YBC,\] so by the inscribed angle theorem $\overline{XY}$ bisects $\angle DXC$.

Claim: $AB^2 = DY \cdot YC$.

Proof. Define the linear function $f(\bullet) := \text{Pow}(\bullet, (ADY)) - \text{Pow}(\bullet, (ABCD))$. Since $\overline{BY}$ is parallel to the radical axis $\overline{AD}$ of $(ADY)$ and $(ABCD)$ by our previous parallelism, $f(B)=f(Y)$. Note that $f(B)=AB^2$ while $f(Y)=DY \cdot YC$, so we conclude. $\square$

By Stewart's theorem on $\triangle DXC$, $DY \cdot YC=37 \cdot 67 - 47^2 = 270$, so $AB^2=\boxed{270}$.

~ Leo.Euler

Video Solution by MOP 2024

https://youtu.be/qFfgB15fYS8

~r00tsOfUnity

Video Solution

https://youtu.be/QoVIorvv_I8

~MathProblemSolvingSkills.com

Video Solution by The Power of Logic

https://youtu.be/lTZx6tp2Fvg

See Also

2016 AIME I (Problems • Answer Key • Resources)
Preceded by
Problem 14 		Followed by
Last Question
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2016_AIME_I_Problems/Problem_15&oldid=210195"