Difference between revisions of "2019 USAMO Problems/Problem 2"
(→Solution 2) |
(→Solution) |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 30: | Line 30: | ||
Since <math>P</math> is the isogonal conjugate of <math>N</math>, <math>\measuredangle PEA = \measuredangle MEC = \measuredangle BEN</math>. However <math>\measuredangle MEC = \measuredangle BEN</math> implies that <math>M</math> is the midpoint of <math>CD</math> from similar triangles, so we are done. <math>\square</math> | Since <math>P</math> is the isogonal conjugate of <math>N</math>, <math>\measuredangle PEA = \measuredangle MEC = \measuredangle BEN</math>. However <math>\measuredangle MEC = \measuredangle BEN</math> implies that <math>M</math> is the midpoint of <math>CD</math> from similar triangles, so we are done. <math>\square</math> | ||
| − | |||
| − | |||
==Solution 2== | ==Solution 2== | ||
| Line 37: | Line 35: | ||
[[File:2019 USAMO 2a.png|450px|right]] | [[File:2019 USAMO 2a.png|450px|right]] | ||
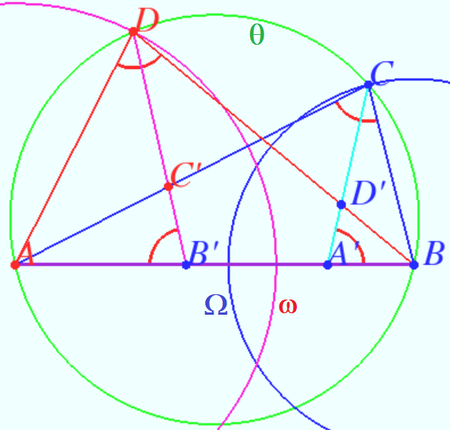
Let <math>\omega</math> be the circle centered at <math>A</math> with radius <math>AD.</math> | Let <math>\omega</math> be the circle centered at <math>A</math> with radius <math>AD.</math> | ||
| + | |||
Let <math>\Omega</math> be the circle centered at <math>B</math> with radius <math>BC.</math> | Let <math>\Omega</math> be the circle centered at <math>B</math> with radius <math>BC.</math> | ||
| − | We denote <math>I_\omega</math> and <math> | + | |
| + | We denote <math>I_\omega</math> and <math>I_\Omega</math> inversion with respect to <math>\omega</math> and <math>\Omega,</math> respectively. | ||
<cmath>B'= I_\omega (B), C'= I_\omega (C), D = I_\omega (D) \implies</cmath> | <cmath>B'= I_\omega (B), C'= I_\omega (C), D = I_\omega (D) \implies</cmath> | ||
<cmath>AB' \cdot AB = AD^2, \angle ACB = \angle AB'C'.</cmath> | <cmath>AB' \cdot AB = AD^2, \angle ACB = \angle AB'C'.</cmath> | ||
| − | <cmath>A'= I_\Omega (A), D'= I_\Omega (D), C = I_\ | + | <cmath>A'= I_\Omega (A), D'= I_\Omega (D), C = I_\Omega (C) \implies</cmath> |
| − | <cmath> | + | <cmath>BA' \cdot AB = BC^2, \angle BDA = \angle BA'D'.</cmath> |
Let <math>\theta</math> be the circle <math>ABCD.</math> | Let <math>\theta</math> be the circle <math>ABCD.</math> | ||
| Line 49: | Line 49: | ||
<cmath>\angle BA'D' = \angle BA'C = \angle BDA.</cmath> | <cmath>\angle BA'D' = \angle BA'C = \angle BDA.</cmath> | ||
<math>ABCD</math> is cyclic <math>\implies \angle BA'C = \angle AB'D.</math> | <math>ABCD</math> is cyclic <math>\implies \angle BA'C = \angle AB'D.</math> | ||
| − | < | + | <cmath>AB' + BA' = \frac {AD^2 + BC^2 }{AB} = AB \implies</cmath> points <math>A'</math> and <math>B'</math> are coincide. |
Denote <math>A' = B' = Q \in AB.</math> | Denote <math>A' = B' = Q \in AB.</math> | ||
| − | Suppose, we move <math> | + | Suppose, we move point <math>Q</math> from <math>A</math> to <math>B.</math> Then <math>\angle AQD</math> decreases monotonically, <math>\angle BQC</math> increases monotonically. So, there is only one point where <cmath>\angle AQD = \angle BQC \implies P = Q.</cmath> |
<cmath>B = I_\omega (P), D' = I_\omega (D'), C' = I_\omega (C), A = I_\omega (\infty) \implies</cmath> | <cmath>B = I_\omega (P), D' = I_\omega (D'), C' = I_\omega (C), A = I_\omega (\infty) \implies</cmath> | ||
| − | <math>\hspace{ | + | <math>\hspace{19mm} I_\omega (CD'P) = AC'D'B</math> is cyclic. |
<cmath>\angle ACD = \angle ABD = \angle CC'D \implies C' D' || CD \implies</cmath> | <cmath>\angle ACD = \angle ABD = \angle CC'D \implies C' D' || CD \implies</cmath> | ||
| − | <math>\hspace{ | + | <math>\hspace{19mm} C'D'CD</math> is trapezoid. |
It is known that the intersection of the diagonals, intersection point of the lines containing the lateral sides of the trapezoid and the midpoints of two parallel sides are collinear. | It is known that the intersection of the diagonals, intersection point of the lines containing the lateral sides of the trapezoid and the midpoints of two parallel sides are collinear. | ||
| Line 66: | Line 66: | ||
==See also== | ==See also== | ||
{{USAMO newbox|year=2019|num-b=1|num-a=3}} | {{USAMO newbox|year=2019|num-b=1|num-a=3}} | ||
| + | |||
| + | {{MAA Notice}} | ||
Latest revision as of 21:51, 18 October 2022
Contents
Problem
Let ![]() be a cyclic quadrilateral satisfying
be a cyclic quadrilateral satisfying ![]() . The diagonals of
. The diagonals of ![]() intersect at
intersect at ![]() . Let
. Let ![]() be a point on side
be a point on side ![]() satisfying
satisfying ![]() . Show that line
. Show that line ![]() bisects
bisects ![]() .
.
Solution
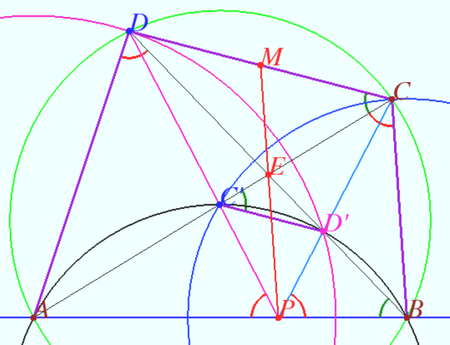
Let ![]() . Also, let
. Also, let ![]() be the midpoint of
be the midpoint of ![]() .
Note that only one point
.
Note that only one point ![]() satisfies the given angle condition. With this in mind, construct
satisfies the given angle condition. With this in mind, construct ![]() with the following properties:
with the following properties:
(1) ![]()
(2) ![]()
Claim: ![]()
Proof:
The conditions imply the similarities ![]() and
and ![]() whence
whence ![]() as desired.
as desired. ![]()
Claim: ![]() is a symmedian in
is a symmedian in ![]()
Proof:
We have
 as desired.
as desired. ![]()
Since ![]() is the isogonal conjugate of
is the isogonal conjugate of ![]() ,
, ![]() . However
. However ![]() implies that
implies that ![]() is the midpoint of
is the midpoint of ![]() from similar triangles, so we are done.
from similar triangles, so we are done. ![]()
Solution 2
Let ![]() be the circle centered at
be the circle centered at ![]() with radius
with radius ![]()
Let ![]() be the circle centered at
be the circle centered at ![]() with radius
with radius ![]()
We denote ![]() and
and ![]() inversion with respect to
inversion with respect to ![]() and
and ![]() respectively.
respectively.
![]()
![]()
![]()
![]() Let
Let ![]() be the circle
be the circle ![]()
![]() straight line, therefore
straight line, therefore ![]()
![]() straight line, therefore
straight line, therefore
![]()
![]() is cyclic
is cyclic ![]()
![]() points
points ![]() and
and ![]() are coincide.
are coincide.
Denote ![]()
Suppose, we move point ![]() from
from ![]() to
to ![]() Then
Then ![]() decreases monotonically,
decreases monotonically, ![]() increases monotonically. So, there is only one point where
increases monotonically. So, there is only one point where ![]()
![]()
![]() is cyclic.
is cyclic.
![]()
![]() is trapezoid.
is trapezoid.
It is known that the intersection of the diagonals, intersection point of the lines containing the lateral sides of the trapezoid and the midpoints of two parallel sides are collinear.
vladimir.shelomovskii@gmail.com, vvsss
See also
| 2019 USAMO (Problems • Resources) | ||
| Preceded by Problem 1 |
Followed by Problem 3 | |
| 1 • 2 • 3 • 4 • 5 • 6 | ||
| All USAMO Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.