Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2024 AIME II Problems/Problem 8"
 
(14 intermediate revisions by 7 users not shown)
Line 1: Line 1:
−
Torus <math>T</math> is the surface produced by revolving a circle with radius 3 around an axis in the plane of the circle that is a distance 6 from the center of the circle (so like a donut). Let <math>S</math> be a sphere with a radius 11. When <math>T</math> rests on the outside of <math>S</math>, it is externally tangent to <math>S</math> along a circle with radius <math>r_i</math>, and when <math>T</math> rests on the outside of <math>S</math>, it is externally tangent to <math>S</math> along a circle with radius <math>r_o</math>. The difference <math>r_i-r_o</math> can be written as <math>\frac{m}{n}</math>, where <math>m</math> and <math>n</math> are relatively prime positive integers. Find <math>m+n</math>.
+
==Problem==
 +
Torus <math>T</math> is the surface produced by revolving a circle with radius <math>3</math> around an axis in the plane of the circle that is a distance <math>6</math> from the center of the circle (so like a donut). Let <math>S</math> be a sphere with a radius <math>11</math>. When <math>T</math> rests on the inside of <math>S</math>, it is internally tangent to <math>S</math> along a circle with radius <math>r_i</math>, and when <math>T</math> rests on the outside of <math>S</math>, it is externally tangent to <math>S</math> along a circle with radius <math>r_o</math>. The difference <math>r_i-r_o</math> can be written as <math>\tfrac{m}{n}</math>, where <math>m</math> and <math>n</math> are relatively prime positive integers. Find <math>m+n</math>.
 +
 
 +
<asy>
 +
unitsize(0.3 inch);
 +
draw(ellipse((0,0), 3, 1.75));
 +
draw((-1.2,0.1)..(-0.8,-0.03)..(-0.4,-0.11)..(0,-0.15)..(0.4,-0.11)..(0.8,-0.03)..(1.2,0.1));
 +
draw((-1,0.04)..(-0.5,0.12)..(0,0.16)..(0.5,0.12)..(1,0.04));
 +
draw((0,2.4)--(0,-0.15));
 +
draw((0,-0.15)--(0,-1.75), dashed);
 +
draw((0,-1.75)--(0,-2.25));
 +
draw(ellipse((2,0), 1, 0.9));
 +
draw((2.03,-0.02)--(2.9,-0.4));
 +
</asy>
 +
 
 +
==Solution 1==
 +
First, let's consider a section <math>\mathcal{P} </math> of the solids, along the axis.
 +
By some 3D-Geomerty thinking, we can simply know that the axis crosses the sphere center. So, that is saying, the <math>\mathcal{P} </math> we took crosses one of the equator of the sphere.
 +
 
 +
Here I drew two graphs, the first one is the case when <math>T</math> is internally tangent to <math>S</math>,
 +
 
 +
<asy>
 +
unitsize(0.35cm);
 +
pair O = (0, 0);
 +
real r1 = 11;
 +
real r2 = 3;
 +
draw(circle(O, r1));
 +
pair A = O + (0, -r1);
 +
pair B = O + (0, r1);
 +
draw(A--B);
 +
pair C = O + (0, -1.25*r1);
 +
pair D = O + (0, 1.25*r1);
 +
draw(C--D, dashed);
 +
dot(O);
 +
pair E = (2 * r2, -sqrt((r1 - r2) * (r1 - r2) - 4 * r2 * r2));
 +
pair F = (0, -sqrt((r1 - r2) * (r1 - r2) - 4 * r2 * r2));
 +
pair G = (-r2 * O + r1 * E) / (r1 - r2);
 +
pair H = (-r2 * O + r1 * F) / (r1 - r2);
 +
draw(circle(E, r2));
 +
draw(circle((-2 * r2, -sqrt((r1 - r2) * (r1 - r2) - 4 * r2 * r2)), r2));
 +
draw(O--G, dashed);
 +
draw(F--E, dashed);
 +
draw(G--H, dashed);
 +
label("$O$", O, SW);
 +
label("$A$", A, SW);
 +
label("$B$", B, NW);
 +
label("$C$", C, NW);
 +
label("$D$", D, SW);
 +
label("$E_i$", E, NE);
 +
label("$F_i$", F, W);
 +
label("$G_i$", G, SE);
 +
label("$H_i$", H, W);
 +
label("$r_i$", 0.5 * H + 0.5 * G, NE);
 +
label("$3$", 0.5 * E + 0.5 * G, NE);
 +
label("$11$", 0.5 * O + 0.5 * G, NE);
 +
</asy>
 +
 
 +
and the second one is when <math>T</math> is externally tangent to <math>S</math>.
 +
 
 +
<asy>
 +
unitsize(0.35cm);
 +
pair O = (0, 0);
 +
real r1 = 11;
 +
real r2 = 3;
 +
draw(circle(O, r1));
 +
pair A = O + (0, -r1);
 +
pair B = O + (0, r1);
 +
draw(A--B);
 +
pair C = O + (0, -1.25*(r1 + r2));
 +
pair D = O + (0, 1.25*r1);
 +
draw(C--D, dashed);
 +
dot(O);
 +
pair E = (2 * r2, -sqrt((r1 + r2) * (r1 + r2) - 4 * r2 * r2));
 +
pair F = (0, -sqrt((r1 + r2) * (r1 + r2) - 4 * r2 * r2));
 +
pair G = (r2 * O + r1 * E) / (r1 + r2);
 +
pair H = (r2 * O + r1 * F) / (r1 + r2);
 +
draw(circle(E, r2));
 +
draw(circle((-2 * r2, -sqrt((r1 + r2) * (r1 + r2) - 4 * r2 * r2)), r2));
 +
draw(O--E, dashed);
 +
draw(F--E, dashed);
 +
draw(G--H, dashed);
 +
label("$O$", O, SW);
 +
label("$A$", A, SW);
 +
label("$B$", B, NW);
 +
label("$C$", C, NW);
 +
label("$D$", D, SW);
 +
label("$E_o$", E, NE);
 +
label("$F_o$", F, SW);
 +
label("$G_o$", G, S);
 +
label("$H_o$", H, W);
 +
label("$r_o$", 0.5 * H + 0.5 * G, NE);
 +
label("$3$", 0.5 * E + 0.5 * G, NE);
 +
label("$11$", 0.5 * O + 0.5 * G, NE);
 +
</asy>
 +
 
 +
For both graphs, point <math>O</math> is the center of sphere <math>S</math>, and points <math>A</math> and <math>B</math> are the intersections of the sphere and the axis. Point <math>E</math> (ignoring the subscripts) is one of the circle centers of the intersection of torus <math>T</math> with section <math>\mathcal{P} </math>. Point <math>G</math> (again, ignoring the subscripts) is one of the tangents between the torus <math>T</math> and sphere <math>S</math> on section <math>\mathcal{P} </math>. <math>EF\bot CD</math>, <math>HG\bot CD</math>.
 +
 
 +
And then, we can start our calculation.
 +
 
 +
In both cases, we know <math>\Delta OEF\sim \Delta OGH\Longrightarrow \frac{EF}{OE} =\frac{GH}{OG}</math>.
 +
 
 +
Hence, in the case of internal tangent, <math>\frac{E_iF_i}{OE_i} =\frac{G_iH_i}{OG_i}\Longrightarrow \frac{6}{11-3} =\frac{r_i}{11}\Longrightarrow r_i=\frac{33}{4} </math>.
 +
 
 +
In the case of external tangent, <math>\frac{E_oF_o}{OE_o} =\frac{G_oH_o}{OG_o}\Longrightarrow \frac{6}{11+3} =\frac{r_o}{11}\Longrightarrow r_o=\frac{33}{7} </math>.
 +
 
 +
Thereby, <math>r_i-r_o=\frac{33}{4}-\frac{33}{7}=\frac{99}{28}</math>. And there goes the answer, <math>99+28=\boxed{\mathbf{127} }</math>
 +
 
 +
~Prof_Joker
 +
==Solution 2==
 +
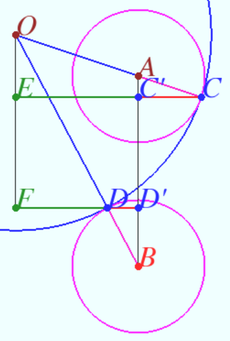
[[File:2024 AIME II 8.png|230px|right]]
 +
<cmath>OC = OD = 11, AC = BD =  3, EC' = FD' = 6.</cmath>
 +
<cmath>\frac {CC'}{C'E} = \frac{AC}{OA} \implies CC' = \frac {3 \cdot 6}{11-3}</cmath>
 +
<cmath>\frac {DD'}{DB} = \frac{FD'}{OB} \implies DD' = \frac {3 \cdot 6}{11+3}</cmath>
 +
<cmath>CC' + DD' = \frac {9}{4}+\frac {9}{7} = \frac {99}{28}.</cmath>
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
 
 +
==Video Solution==
 +
 
 +
https://youtu.be/-1HLRjtLCSM
 +
 
 +
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
 +
 
 +
==Video Solution（中文）subtitle in English ==
 +
https://youtu.be/YdQdDBROG8U
 +
 
 +
==See also==
 +
{{AIME box|year=2024|num-b=7|num-a=9|n=II}}
 +
 
 +
[[Category:Intermediate Geometry Problems]]
 +
{{MAA Notice}}

Latest revision as of 19:31, 22 October 2024

Problem

Torus $T$ is the surface produced by revolving a circle with radius $3$ around an axis in the plane of the circle that is a distance $6$ from the center of the circle (so like a donut). Let $S$ be a sphere with a radius $11$. When $T$ rests on the inside of $S$, it is internally tangent to $S$ along a circle with radius $r_i$, and when $T$ rests on the outside of $S$, it is externally tangent to $S$ along a circle with radius $r_o$. The difference $r_i-r_o$ can be written as $\tfrac{m}{n}$, where $m$ and $n$ are relatively prime positive integers. Find $m+n$.

[asy] unitsize(0.3 inch); draw(ellipse((0,0), 3, 1.75)); draw((-1.2,0.1)..(-0.8,-0.03)..(-0.4,-0.11)..(0,-0.15)..(0.4,-0.11)..(0.8,-0.03)..(1.2,0.1)); draw((-1,0.04)..(-0.5,0.12)..(0,0.16)..(0.5,0.12)..(1,0.04)); draw((0,2.4)--(0,-0.15)); draw((0,-0.15)--(0,-1.75), dashed); draw((0,-1.75)--(0,-2.25)); draw(ellipse((2,0), 1, 0.9)); draw((2.03,-0.02)--(2.9,-0.4)); [/asy]

Solution 1

First, let's consider a section $\mathcal{P}$ of the solids, along the axis. By some 3D-Geomerty thinking, we can simply know that the axis crosses the sphere center. So, that is saying, the $\mathcal{P}$ we took crosses one of the equator of the sphere.

Here I drew two graphs, the first one is the case when $T$ is internally tangent to $S$,

[asy] unitsize(0.35cm); pair O = (0, 0); real r1 = 11; real r2 = 3; draw(circle(O, r1)); pair A = O + (0, -r1); pair B = O + (0, r1); draw(A--B); pair C = O + (0, -1.25*r1); pair D = O + (0, 1.25*r1); draw(C--D, dashed); dot(O); pair E = (2 * r2, -sqrt((r1 - r2) * (r1 - r2) - 4 * r2 * r2)); pair F = (0, -sqrt((r1 - r2) * (r1 - r2) - 4 * r2 * r2)); pair G = (-r2 * O + r1 * E) / (r1 - r2); pair H = (-r2 * O + r1 * F) / (r1 - r2); draw(circle(E, r2)); draw(circle((-2 * r2, -sqrt((r1 - r2) * (r1 - r2) - 4 * r2 * r2)), r2)); draw(O--G, dashed); draw(F--E, dashed); draw(G--H, dashed); label("$O$", O, SW); label("$A$", A, SW); label("$B$", B, NW); label("$C$", C, NW); label("$D$", D, SW); label("$E_i$", E, NE); label("$F_i$", F, W); label("$G_i$", G, SE); label("$H_i$", H, W); label("$r_i$", 0.5 * H + 0.5 * G, NE); label("$3$", 0.5 * E + 0.5 * G, NE); label("$11$", 0.5 * O + 0.5 * G, NE); [/asy]

and the second one is when $T$ is externally tangent to $S$.

[asy] unitsize(0.35cm); pair O = (0, 0); real r1 = 11; real r2 = 3; draw(circle(O, r1)); pair A = O + (0, -r1); pair B = O + (0, r1); draw(A--B); pair C = O + (0, -1.25*(r1 + r2)); pair D = O + (0, 1.25*r1); draw(C--D, dashed); dot(O); pair E = (2 * r2, -sqrt((r1 + r2) * (r1 + r2) - 4 * r2 * r2)); pair F = (0, -sqrt((r1 + r2) * (r1 + r2) - 4 * r2 * r2)); pair G = (r2 * O + r1 * E) / (r1 + r2); pair H = (r2 * O + r1 * F) / (r1 + r2); draw(circle(E, r2)); draw(circle((-2 * r2, -sqrt((r1 + r2) * (r1 + r2) - 4 * r2 * r2)), r2)); draw(O--E, dashed); draw(F--E, dashed); draw(G--H, dashed); label("$O$", O, SW); label("$A$", A, SW); label("$B$", B, NW); label("$C$", C, NW); label("$D$", D, SW); label("$E_o$", E, NE); label("$F_o$", F, SW); label("$G_o$", G, S); label("$H_o$", H, W); label("$r_o$", 0.5 * H + 0.5 * G, NE); label("$3$", 0.5 * E + 0.5 * G, NE); label("$11$", 0.5 * O + 0.5 * G, NE); [/asy]

For both graphs, point $O$ is the center of sphere $S$, and points $A$ and $B$ are the intersections of the sphere and the axis. Point $E$ (ignoring the subscripts) is one of the circle centers of the intersection of torus $T$ with section $\mathcal{P}$. Point $G$ (again, ignoring the subscripts) is one of the tangents between the torus $T$ and sphere $S$ on section $\mathcal{P}$. $EF\bot CD$, $HG\bot CD$.

And then, we can start our calculation.

In both cases, we know $\Delta OEF\sim \Delta OGH\Longrightarrow \frac{EF}{OE} =\frac{GH}{OG}$.

Hence, in the case of internal tangent, $\frac{E_iF_i}{OE_i} =\frac{G_iH_i}{OG_i}\Longrightarrow \frac{6}{11-3} =\frac{r_i}{11}\Longrightarrow r_i=\frac{33}{4}$.

In the case of external tangent, $\frac{E_oF_o}{OE_o} =\frac{G_oH_o}{OG_o}\Longrightarrow \frac{6}{11+3} =\frac{r_o}{11}\Longrightarrow r_o=\frac{33}{7}$.

Thereby, $r_i-r_o=\frac{33}{4}-\frac{33}{7}=\frac{99}{28}$. And there goes the answer, $99+28=\boxed{\mathbf{127} }$

~Prof_Joker

Solution 2

2024 AIME II 8.png

\[OC = OD = 11, AC = BD = 3, EC' = FD' = 6.\] \[\frac {CC'}{C'E} = \frac{AC}{OA} \implies CC' = \frac {3 \cdot 6}{11-3}\] \[\frac {DD'}{DB} = \frac{FD'}{OB} \implies DD' = \frac {3 \cdot 6}{11+3}\] \[CC' + DD' = \frac {9}{4}+\frac {9}{7} = \frac {99}{28}.\] vladimir.shelomovskii@gmail.com, vvsss

Video Solution

https://youtu.be/-1HLRjtLCSM

~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

Video Solution（中文）subtitle in English

https://youtu.be/YdQdDBROG8U

See also

2024 AIME II (Problems • Answer Key • Resources)
Preceded by
Problem 7 		Followed by
Problem 9
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2024_AIME_II_Problems/Problem_8&oldid=230369"