Difference between revisions of "Cyclic quadrilateral"
Scrabbler94 (talk | contribs) (Undo revision 215841 by Marianasinta (talk)) (Tag: Undo) |
(→Problems) |
||
| (8 intermediate revisions by 3 users not shown) | |||
| Line 7: | Line 7: | ||
In a quadrilateral <math>ABCD</math>: | In a quadrilateral <math>ABCD</math>: | ||
| − | * <math>\angle A + \angle C = \angle B + \angle D = {180}^{o} </math> This property is both sufficient and necessary, and is often used to show that a quadrilateral is cyclic. | + | * <math>\angle A + \angle C = \angle B + \angle D = {180}^{o} </math> This property is both sufficient and necessary (Sufficient & necessary = if and only if), and is often used to show that a quadrilateral is cyclic. |
* <math>\angle ABD = \angle ACD</math> | * <math>\angle ABD = \angle ACD</math> | ||
* <math>\angle BCA = \angle BDA</math> | * <math>\angle BCA = \angle BDA</math> | ||
| Line 14: | Line 14: | ||
* All four [[perpendicular bisector|perpendicular bisectors]] are [[concurrent]]. The converse is also true. This intersection is the [[circumcenter]] of the quadrilateral. | * All four [[perpendicular bisector|perpendicular bisectors]] are [[concurrent]]. The converse is also true. This intersection is the [[circumcenter]] of the quadrilateral. | ||
* Any two opposite sites of the quadrilateral are antiparallel with respect to the other two opposite sites. | * Any two opposite sites of the quadrilateral are antiparallel with respect to the other two opposite sites. | ||
| − | |||
== Applicable Theorems/Formulae == | == Applicable Theorems/Formulae == | ||
| Line 22: | Line 21: | ||
* [[Ptolemy's Theorem]] | * [[Ptolemy's Theorem]] | ||
* [[Brahmagupta's formula]] | * [[Brahmagupta's formula]] | ||
| + | |||
| + | == Problems == | ||
| + | |||
| + | === Intermediate/Advanced === | ||
| + | * [[1991 AIME Problems/Problem 12]] | ||
| + | * [[2001 AIME I Problems/Problem 13]] | ||
| + | * [[2000 AIME I Problems/Problem 14]] | ||
| + | * [[1997 AIME Problems/Problem 15]] | ||
[[Category:Definition]] | [[Category:Definition]] | ||
Latest revision as of 18:41, 3 January 2025
A cyclic quadrilateral is a quadrilateral that can be inscribed in a circle. While all triangles are cyclic, the same is not true of quadrilaterals. They have a number of interesting properties.
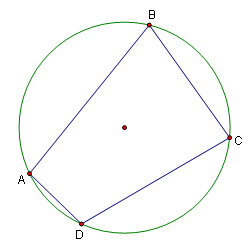
Properties
In a quadrilateral ![]() :
:
 This property is both sufficient and necessary (Sufficient & necessary = if and only if), and is often used to show that a quadrilateral is cyclic.
This property is both sufficient and necessary (Sufficient & necessary = if and only if), and is often used to show that a quadrilateral is cyclic.



- All four perpendicular bisectors are concurrent. The converse is also true. This intersection is the circumcenter of the quadrilateral.
- Any two opposite sites of the quadrilateral are antiparallel with respect to the other two opposite sites.
Applicable Theorems/Formulae
The following theorems and formulae apply to cyclic quadrilaterals:
Problems
Intermediate/Advanced
- 1991 AIME Problems/Problem 12
- 2001 AIME I Problems/Problem 13
- 2000 AIME I Problems/Problem 14
- 1997 AIME Problems/Problem 15
This article is a stub. Help us out by expanding it.









