Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2008 IMO Problems/Problem 1"

m
 
(One intermediate revision by one other user not shown)
Line 4: Line 4:
 
== Solution ==
 
== Solution ==
  
−
[[Image:IMO20081.png|right|100px]]
+
[[Image:IMO20081.png|right|500px]]
  
 
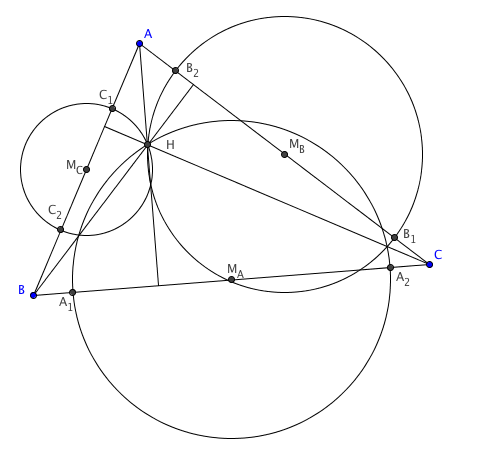
Let <math>M_A</math>, <math>M_B</math>, and <math>M_C</math> be the midpoints of sides <math>BC</math>, <math>CA</math>, and <math>AB</math>, respectively. It's not hard to see that <math>M_BM_C\parallel BC</math>. We also have that <math>AH\perp BC</math>, so <math>AH \perp M_BM_C</math>. Now note that the radical axis of two circles is perpendicular to the line connecting their centers. We know that <math>H</math> is on the radical axis of the circles centered at <math>M_B</math> and <math>M_C</math>, so <math>A</math> is too. We then have <math>AC_1\cdot AC_2=AB_2\cdot AB_1\Rightarrow \frac{AB_2}{AC_1}=\frac{AC_2}{AB_1}</math>. This implies that <math>\triangle AB_2C_1\sim \triangle AC_2B_1</math>, so <math>\angle AB_2C_1=\angle AC_2B_1</math>. Therefore <math>\angle C_1B_2B_1=180^{\circ}-\angle AB_2C_1=180^{\circ}-\angle AC_2B_1</math>. This shows that quadrilateral <math>C_1C_2B_1B_2</math> is cyclic. Note that the center of its circumcircle is at the intersection of the perpendicular bisectors of the segments <math>C_1C_2</math> and <math>B_1B_2</math>. However, these are just the perpendicular bisectors of <math>AB</math> and <math>CA</math>, which meet at the circumcenter of <math>ABC</math>, so the circumcenter of <math>C_1C_2B_1B_2</math> is the circumcenter of triangle <math>ABC</math>. Similarly, the circumcenters of <math>A_1A_2B_1B_2</math> and <math>C_1C_2A_1A_2</math> are coincident with the circumcenter of <math>ABC</math>. The desired result follows.
 
Let <math>M_A</math>, <math>M_B</math>, and <math>M_C</math> be the midpoints of sides <math>BC</math>, <math>CA</math>, and <math>AB</math>, respectively. It's not hard to see that <math>M_BM_C\parallel BC</math>. We also have that <math>AH\perp BC</math>, so <math>AH \perp M_BM_C</math>. Now note that the radical axis of two circles is perpendicular to the line connecting their centers. We know that <math>H</math> is on the radical axis of the circles centered at <math>M_B</math> and <math>M_C</math>, so <math>A</math> is too. We then have <math>AC_1\cdot AC_2=AB_2\cdot AB_1\Rightarrow \frac{AB_2}{AC_1}=\frac{AC_2}{AB_1}</math>. This implies that <math>\triangle AB_2C_1\sim \triangle AC_2B_1</math>, so <math>\angle AB_2C_1=\angle AC_2B_1</math>. Therefore <math>\angle C_1B_2B_1=180^{\circ}-\angle AB_2C_1=180^{\circ}-\angle AC_2B_1</math>. This shows that quadrilateral <math>C_1C_2B_1B_2</math> is cyclic. Note that the center of its circumcircle is at the intersection of the perpendicular bisectors of the segments <math>C_1C_2</math> and <math>B_1B_2</math>. However, these are just the perpendicular bisectors of <math>AB</math> and <math>CA</math>, which meet at the circumcenter of <math>ABC</math>, so the circumcenter of <math>C_1C_2B_1B_2</math> is the circumcenter of triangle <math>ABC</math>. Similarly, the circumcenters of <math>A_1A_2B_1B_2</math> and <math>C_1C_2A_1A_2</math> are coincident with the circumcenter of <math>ABC</math>. The desired result follows.
 +
 +
==See Also==
 +
 +
{{IMO box|year=2008|before=First Problem|num-a=2}}

Latest revision as of 00:08, 19 November 2023

Problem

An acute-angled triangle $ABC$ has orthocentre $H$. The circle passing through $H$ with centre the midpoint of $BC$ intersects the line $BC$ at $A_1$ and $A_2$. Similarly, the circle passing through $H$ with centre the midpoint of $CA$ intersects the line $CA$ at $B_1$ and $B_2$, and the circle passing through $H$ with centre the midpoint of $AB$ intersects the line $AB$ at $C_1$ and $C_2$. Show that $A_1$, $A_2$, $B_1$, $B_2$, $C_1$, $C_2$ lie on a circle.

Solution

IMO20081.png

Let $M_A$, $M_B$, and $M_C$ be the midpoints of sides $BC$, $CA$, and $AB$, respectively. It's not hard to see that $M_BM_C\parallel BC$. We also have that $AH\perp BC$, so $AH \perp M_BM_C$. Now note that the radical axis of two circles is perpendicular to the line connecting their centers. We know that $H$ is on the radical axis of the circles centered at $M_B$ and $M_C$, so $A$ is too. We then have $AC_1\cdot AC_2=AB_2\cdot AB_1\Rightarrow \frac{AB_2}{AC_1}=\frac{AC_2}{AB_1}$. This implies that $\triangle AB_2C_1\sim \triangle AC_2B_1$, so $\angle AB_2C_1=\angle AC_2B_1$. Therefore $\angle C_1B_2B_1=180^{\circ}-\angle AB_2C_1=180^{\circ}-\angle AC_2B_1$. This shows that quadrilateral $C_1C_2B_1B_2$ is cyclic. Note that the center of its circumcircle is at the intersection of the perpendicular bisectors of the segments $C_1C_2$ and $B_1B_2$. However, these are just the perpendicular bisectors of $AB$ and $CA$, which meet at the circumcenter of $ABC$, so the circumcenter of $C_1C_2B_1B_2$ is the circumcenter of triangle $ABC$. Similarly, the circumcenters of $A_1A_2B_1B_2$ and $C_1C_2A_1A_2$ are coincident with the circumcenter of $ABC$. The desired result follows.

See Also

2008 IMO (Problems) • Resources
Preceded by
First Problem 		1 • 2 • 3 • 4 • 5 • 6 Followed by
Problem 2
All IMO Problems and Solutions
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2008_IMO_Problems/Problem_1&oldid=204528"