Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1988 AIME Problems/Problem 12"
m
 
(6 intermediate revisions by 5 users not shown)
Line 4: Line 4:
 
[[Image:1988_AIME-12.png]]
 
[[Image:1988_AIME-12.png]]
  
−
== Solution ==
+
== Solution 1 ==
 
Call the [[cevian]]s AD, BE, and CF. Using area ratios (<math>\triangle PBC</math> and <math>\triangle ABC</math> have the same base), we have:  
 
Call the [[cevian]]s AD, BE, and CF. Using area ratios (<math>\triangle PBC</math> and <math>\triangle ABC</math> have the same base), we have:  
  
Line 22: Line 22:
 
<cmath>3(ab + bc + ca) + 18(a + b + c) + 81 = abc + 3(ab + bc + ca) + 9(a + b + c) + 27</cmath>
 
<cmath>3(ab + bc + ca) + 18(a + b + c) + 81 = abc + 3(ab + bc + ca) + 9(a + b + c) + 27</cmath>
 
<cmath>9(a + b + c) + 54 = abc=\boxed{441}</cmath>
 
<cmath>9(a + b + c) + 54 = abc=\boxed{441}</cmath>
 +
 +
==Solution 2==
 +
 +
Let <math>A,B,C</math> be the weights of the respective vertices. We see that the weights of the feet of the cevians are <math>A+B,B+C,C+A</math>. By [[mass points]], we have that: <cmath>\dfrac{a}{3}=\dfrac{B+C}{A}</cmath> <cmath>\dfrac{b}{3}=\dfrac{C+A}{B}</cmath> <cmath>\dfrac{c}{3}=\dfrac{A+B}{C}</cmath>
 +
 +
If we add the equations together, we get <math>\frac{a+b+c}{3}=\frac{A^2B+A^2C+B^2A+B^2C+C^2A+C^2B}{ABC}=\frac{43}{3}</math>
 +
 +
If we multiply them together, we get <math>\frac{abc}{27}=\frac{A^2B+A^2C+B^2A+B^2C+C^2A+C^2B+2ABC}{ABC}=\frac{49}{3} \implies abc=\boxed{441}</math>
 +
 +
==Solution 3==
 +
 +
You can use mass points to derive <math>\frac {d}{a + d} + \frac {d}{b + d} + \frac {d}{c + d}=1.</math> Plugging it in yields <math>\frac{3}{a + 3} + \frac{3}{b + 3} + \frac{3}{c+3} = 1.</math> We proceed as we did in Solution 1 - however, to make the equation look less messy, we do the substitution <math>a'=a+3,b'=b+3,c'=c+3.</math>
 +
 +
Then we have <math>\frac{3}{a'}+\frac{3}{b'}+\frac{3}{c'}=1.</math> Clearing fractions gives us <math>a'b'c'=3a'b'+3b'c'+3c'a'\to a'b'c'-3a'b'-3b'c'-3c'a'=0.</math> Factoring yields <math>(a'-3)(b'-3)(c'-3)=9(a'+b'+c')-27,</math> and the left hand side looks suspiciously like what we want to find. (It is.)
 +
 +
Substituting yields our answer as <math>9\cdot 52-27=\boxed{441}.</math>
 +
 +
== Solution 4 (Ceva Identity) ==
 +
 +
A cool identity derived from Ceva's Theorem is that:
 +
 +
<cmath>\frac{AP}{PA'}\frac{BP}{PB'}\frac{CP}{PC'} = 2 + \frac{AP}{PA'} + \frac{BP}{PB'} + \frac{CP}{PC'}</cmath>
 +
 +
To see this, we use another Ceva's Theorem identity (sometimes attributed to Gergonne): <math>\frac{AP}{PA'}=\frac{AC'}{C'B}+\frac{AB'}{B'C}</math>, and similarly for cevians <math>BB'</math> and <math>CC'</math>.  And then:
 +
 +
<math>\frac{AP}{PA'}\frac{BP}{PB'}\frac{CP}{PC'} =
 +
\left(\frac{AB'}{B'C}+\frac{AC'}{C'B}\right)
 +
\left(\frac{BC'}{C'A}+\frac{BA'}{A'C}\right)
 +
\left(\frac{CB'}{B'A}+\frac{CA'}{A'B}\right) = \\
 +
\underbrace{\frac{AB'\cdot CA'\cdot BC'}{B'C\cdot A'B\cdot C'A}}_{Ceva} +
 +
\underbrace{\frac{AC'\cdot BA'\cdot CB'}{C'B\cdot A'C\cdot B'A}}_{Ceva} +
 +
\underbrace{\frac{AB'}{B'C} + \frac{AC'}{C'B}}_{Gergonne} +
 +
\underbrace{\frac{BA'}{A'C} + \frac{BC'}{C'A}}_{Gergonne} +
 +
\underbrace{\frac{CA'}{A'B} + \frac{CB'}{B'A}}_{Gergonne} = \\
 +
2 + \frac{AP}{PA'} + \frac{BP}{PB'} + \frac{CP}{PC'}</math>
 +
 +
Inserting <math>a, b, c, d</math> into our identity gives:
 +
 +
<cmath>\frac{a}{d}\frac{b}{d}\frac{c}{d}=2+\frac{a}{d}+\frac{b}{d}+\frac{c}{d}\implies abc=d^3(2+\frac{a+b+c}{d})=3^3(2+\frac{43}{3})=\boxed{441}</cmath>
 +
 +
This problem is quite similar to the 1992 AIME problem 14, which also featured concurrent cevians and is trivialized by the identity used in this solution. For reference, below is a link.
 +
https://artofproblemsolving.com/wiki/index.php/1992_AIME_Problems/Problem_14
  
 
== See also ==
 
== See also ==

Latest revision as of 22:37, 7 March 2024

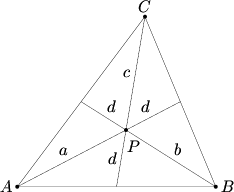
Problem

Let $P$ be an interior point of triangle $ABC$ and extend lines from the vertices through $P$ to the opposite sides. Let $a$, $b$, $c$, and $d$ denote the lengths of the segments indicated in the figure. Find the product $abc$ if $a + b + c = 43$ and $d = 3$.

1988 AIME-12.png

Solution 1

Call the cevians AD, BE, and CF. Using area ratios ($\triangle PBC$ and $\triangle ABC$ have the same base), we have:

$\frac {d}{a + d} = \frac {[PBC]}{[ABC]}$

Similarily, $\frac {d}{b + d} = \frac {[PCA]}{[ABC]}$ and $\frac {d}{c + d} = \frac {[PAB]}{[ABC]}$.

Then, $\frac {d}{a + d} + \frac {d}{b + d} + \frac {d}{c + d} = \frac {[PBC]}{[ABC]} + \frac {[PCA]}{[ABC]} + \frac {[PAB]}{[ABC]} = \frac {[ABC]}{[ABC]} = 1$

The identity $\frac {d}{a + d} + \frac {d}{b + d} + \frac {d}{c + d} = 1$ is a form of Ceva's Theorem.

Plugging in $d = 3$, we get

\[\frac{3}{a + 3} + \frac{3}{b + 3} + \frac{3}{c+3} = 1\] \[3[(a + 3)(b + 3) + (b + 3)(c + 3) + (c + 3)(a + 3)] = (a+3)(b+3)(c+3)\] \[3(ab + bc + ca) + 18(a + b + c) + 81 = abc + 3(ab + bc + ca) + 9(a + b + c) + 27\] \[9(a + b + c) + 54 = abc=\boxed{441}\]

Solution 2

Let $A,B,C$ be the weights of the respective vertices. We see that the weights of the feet of the cevians are $A+B,B+C,C+A$. By mass points, we have that: \[\dfrac{a}{3}=\dfrac{B+C}{A}\] \[\dfrac{b}{3}=\dfrac{C+A}{B}\] \[\dfrac{c}{3}=\dfrac{A+B}{C}\]

If we add the equations together, we get $\frac{a+b+c}{3}=\frac{A^2B+A^2C+B^2A+B^2C+C^2A+C^2B}{ABC}=\frac{43}{3}$

If we multiply them together, we get $\frac{abc}{27}=\frac{A^2B+A^2C+B^2A+B^2C+C^2A+C^2B+2ABC}{ABC}=\frac{49}{3} \implies abc=\boxed{441}$

Solution 3

You can use mass points to derive $\frac {d}{a + d} + \frac {d}{b + d} + \frac {d}{c + d}=1.$ Plugging it in yields $\frac{3}{a + 3} + \frac{3}{b + 3} + \frac{3}{c+3} = 1.$ We proceed as we did in Solution 1 - however, to make the equation look less messy, we do the substitution $a'=a+3,b'=b+3,c'=c+3.$

Then we have $\frac{3}{a'}+\frac{3}{b'}+\frac{3}{c'}=1.$ Clearing fractions gives us $a'b'c'=3a'b'+3b'c'+3c'a'\to a'b'c'-3a'b'-3b'c'-3c'a'=0.$ Factoring yields $(a'-3)(b'-3)(c'-3)=9(a'+b'+c')-27,$ and the left hand side looks suspiciously like what we want to find. (It is.)

Substituting yields our answer as $9\cdot 52-27=\boxed{441}.$

Solution 4 (Ceva Identity)

A cool identity derived from Ceva's Theorem is that:

\[\frac{AP}{PA'}\frac{BP}{PB'}\frac{CP}{PC'} = 2 + \frac{AP}{PA'} + \frac{BP}{PB'} + \frac{CP}{PC'}\]

To see this, we use another Ceva's Theorem identity (sometimes attributed to Gergonne): $\frac{AP}{PA'}=\frac{AC'}{C'B}+\frac{AB'}{B'C}$, and similarly for cevians $BB'$ and $CC'$. And then:

$\frac{AP}{PA'}\frac{BP}{PB'}\frac{CP}{PC'} = \left(\frac{AB'}{B'C}+\frac{AC'}{C'B}\right) \left(\frac{BC'}{C'A}+\frac{BA'}{A'C}\right) \left(\frac{CB'}{B'A}+\frac{CA'}{A'B}\right) = \\ \underbrace{\frac{AB'\cdot CA'\cdot BC'}{B'C\cdot A'B\cdot C'A}}_{Ceva} + \underbrace{\frac{AC'\cdot BA'\cdot CB'}{C'B\cdot A'C\cdot B'A}}_{Ceva} + \underbrace{\frac{AB'}{B'C} + \frac{AC'}{C'B}}_{Gergonne} + \underbrace{\frac{BA'}{A'C} + \frac{BC'}{C'A}}_{Gergonne} + \underbrace{\frac{CA'}{A'B} + \frac{CB'}{B'A}}_{Gergonne} = \\ 2 + \frac{AP}{PA'} + \frac{BP}{PB'} + \frac{CP}{PC'}$

Inserting $a, b, c, d$ into our identity gives:

\[\frac{a}{d}\frac{b}{d}\frac{c}{d}=2+\frac{a}{d}+\frac{b}{d}+\frac{c}{d}\implies abc=d^3(2+\frac{a+b+c}{d})=3^3(2+\frac{43}{3})=\boxed{441}\]

This problem is quite similar to the 1992 AIME problem 14, which also featured concurrent cevians and is trivialized by the identity used in this solution. For reference, below is a link. https://artofproblemsolving.com/wiki/index.php/1992_AIME_Problems/Problem_14

See also

1988 AIME (Problems • Answer Key • Resources)
Preceded by
Problem 11 		Followed by
Problem 13
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1988_AIME_Problems/Problem_12&oldid=216594"