Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2015 AIME I Problems/Problem 6"

(Created page with "==Problem== Point <math>A,B,C,D,</math> and <math>E</math> are equally spaced on a minor arc of a cirle. Points <math>E,F,G,H,I</math> and <math>A</math> are equally spaced on...")
 
m
 
(27 intermediate revisions by 17 users not shown)
Line 1: Line 1:
 
==Problem==
 
==Problem==
−
Point <math>A,B,C,D,</math> and <math>E</math> are equally spaced on a minor arc of a cirle. Points <math>E,F,G,H,I</math> and <math>A</math> are equally spaced on a minor arc of a second circle with center <math>C</math> as shown in the figure below. The angle <math>\angle ABD</math> exceeds <math>\angle AHG</math> by <math>12^\circ</math>. Find the degree measure of <math>\angle BAG</math>.
+
Point <math>A,B,C,D,</math> and <math>E</math> are equally spaced on a minor arc of a circle. Points <math>E,F,G,H,I</math> and <math>A</math> are equally spaced on a minor arc of a second circle with center <math>C</math> as shown in the figure below. The angle <math>\angle ABD</math> exceeds <math>\angle AHG</math> by <math>12^\circ</math>. Find the degree measure of <math>\angle BAG</math>.
 +
 
 +
<asy>
 +
pair A,B,C,D,E,F,G,H,I,O;
 +
O=(0,0);
 +
C=dir(90);
 +
B=dir(70);
 +
A=dir(50);
 +
D=dir(110);
 +
E=dir(130);
 +
draw(arc(O,1,50,130));
 +
real x=2*sin(20*pi/180);
 +
F=x*dir(228)+C;
 +
G=x*dir(256)+C;
 +
H=x*dir(284)+C;
 +
I=x*dir(312)+C;
 +
draw(arc(C,x,200,340));
 +
label("$A$",A,dir(0));
 +
label("$B$",B,dir(75));
 +
label("$C$",C,dir(90));
 +
label("$D$",D,dir(105));
 +
label("$E$",E,dir(180));
 +
label("$F$",F,dir(225));
 +
label("$G$",G,dir(260));
 +
label("$H$",H,dir(280));
 +
label("$I$",I,dir(315));
 +
</asy>
 +
 
 +
==Solution 1==
 +
 
 +
Let <math>O</math> be the center of the circle with <math>ABCDE</math> on it.
 +
 
 +
Let <math>x</math> be the degree measurement of <math>\overarc{ED}=\overarc{DC}=\overarc{CB}=\overarc{BA}</math> in circle <math>O</math>
 +
 
 +
and <math>y</math> be the degree measurement of <math>\overarc{EF}=\overarc{FG}=\overarc{GH}=\overarc{HI}=\overarc{IA}</math> in circle <math>C</math>.
 +
 
 +
<math>\angle ECA</math> is, therefore, <math>5y</math> by way of circle <math>C</math> and <cmath>\frac{360-4x}{2}=180-2x</cmath> by way of circle <math>O</math>.
 +
<math>\angle ABD</math> is <math>180 - \frac{3x}{2}</math> by way of circle <math>O</math>, and <cmath>\angle AHG = 180 - \frac{3y}{2}</cmath> by way of circle <math>C</math>.
 +
 
 +
This means that:
 +
 
 +
<cmath>180-\frac{3x}{2}=180-\frac{3y}{2}+12</cmath>
 +
 
 +
which when simplified yields <cmath>\frac{3x}{2}+12=\frac{3y}{2}</cmath> or <cmath>x+8=y</cmath>
 +
Since:
 +
<cmath>5y=180-2x</cmath> and <cmath>5x+40=180-2x</cmath>
 +
So:
 +
<cmath>7x=140\Longleftrightarrow x=20</cmath>
 +
<cmath>y=28</cmath>
 +
<math>\angle BAG</math> is equal to <math>\angle BAE</math> + <math>\angle EAG</math>, which equates to <math>\frac{3x}{2} + y</math>.
 +
Plugging in yields <math>30+28</math>, or <math>\boxed{058}</math>.
 +
 
 +
==Solution 2==
 +
Let <math>m</math> be the degree measurement of <math>\angle GCH</math>. Since <math>G,H</math> lie on a circle with center <math>C</math>, <math>\angle GHC=\frac{180-m}{2}=90-\frac{m}{2}</math>.
 +
 
 +
Since <math>\angle ACH=2 \angle GCH=2m</math>, <math>\angle AHC=\frac{180-2m}{2}=90-m</math>. Adding <math>\angle GHC</math> and <math>\angle AHC</math> gives <math>\angle AHG=180-\frac{3m}{2}</math>, and <math>\angle ABD=\angle AHG+12=192-\frac{3m}{2}</math>. Since <math>AE</math> is parallel to <math>BD</math>, <math>\angle DBA=180-\angle ABD=\frac{3m}{2}-12=</math><math>\overarc{BE}</math>.
 +
 
 +
We are given that <math>A,B,C,D,E</math> are evenly distributed on a circle. Hence,
 +
 
 +
<math>\overarc{ED}=\overarc{DC}=\overarc{CB}=\overarc{BA}</math><math>=\frac{\angle DBA}{3}=\frac{m}{2}-4</math>
 +
 
 +
Here comes the key: Draw a line through <math>C</math> parallel to <math>AE</math>, and select a point <math>X</math> to the right of point <math>C</math>.
 +
 
 +
<math>\angle ACX</math> = <math>\overarc{AB}</math> + <math>\overarc{BC}</math> = <math>m-8</math>.
 +
 
 +
Let the midpoint of <math>\overline{HG}</math> be <math>Y</math>, then <math>\angle YCX=\angle ACX+\angle ACY=(m-8)+\frac{5m}{2}=90</math>. Solving gives <math>m=28</math>
 +
 
 +
The rest of the solution proceeds as in solution 1, which gives <math>\boxed{058}</math>
 +
 
 +
 
 +
 
 +
==Solution 3==
 +
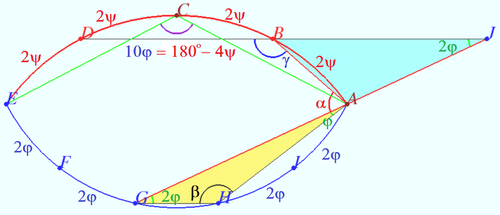
[[File:2015 AIME I 6.png|500px|right]]
 +
Let <math>\angle GAH = \varphi \implies \overset{\Large\frown} {GH} = 2\varphi \implies</math>
 +
<cmath>\overset{\Large\frown} {EF} = \overset{\Large\frown} {FG} = \overset{\Large\frown} {HI} = \overset{\Large\frown} {IA} = 2\varphi \implies</cmath>
 +
<cmath>\angle AGH = 2\varphi, \angle ACE = 10 \varphi.</cmath>
 +
 
 +
<cmath>BD||GH \implies \angle AJB = \angle AGH = 2 \varphi.</cmath>
 +
<cmath>\triangle AHG: \hspace{10mm}  \angle AHG = \beta = 180^\circ – 3 \varphi.</cmath>
 +
<math>\hspace{10mm} \triangle ABJ:  \hspace{10mm} \angle BAG + \angle ABD = \alpha + \gamma = 180^\circ + 2 \varphi. </math>
 +
 
 +
Let arc <math> \overset{\Large\frown} {AB} = 2\psi \implies</math>
 +
 
 +
<math>\angle ACE = \frac {360^\circ – 8 \psi}{2}= 180^\circ – 4 \psi,  \angle ABD = \gamma =\frac {360^\circ – 6 \psi}{2} =180^\circ – 3 \psi.</math>
 +
<math>\gamma –  \beta = 3(\varphi – \psi) = 12^\circ \implies \psi = \varphi – 4^\circ \implies 10 \varphi = 180^\circ – 4(\varphi – 4^\circ) \implies 14 \varphi = 196^\circ \implies \varphi = 14^\circ.</math>
 +
 
 +
Therefore <math>\gamma = 180^\circ – 3 \cdot (14^\circ – 4^\circ) = 150^\circ \implies  \alpha = 180^\circ + 2 \cdot 14^\circ – 150^\circ = \boxed{\textbf{058}}.</math>
 +
 
 +
 
 +
 
 +
==Video Solution==
 +
 
 +
https://youtu.be/IuwkX2Dv25s
 +
 
 +
~MathProblemSolvingSkills.com
 +
 
 +
 
  
 
==See Also==
 
==See Also==
 
{{AIME box|year=2015|n=I|num-b=5|num-a=7}}
 
{{AIME box|year=2015|n=I|num-b=5|num-a=7}}
 
{{MAA Notice}}
 
{{MAA Notice}}
 +
 +
[[Category:Introductory Geometry Problems]]

Latest revision as of 15:04, 21 July 2023

Problem

Point $A,B,C,D,$ and $E$ are equally spaced on a minor arc of a circle. Points $E,F,G,H,I$ and $A$ are equally spaced on a minor arc of a second circle with center $C$ as shown in the figure below. The angle $\angle ABD$ exceeds $\angle AHG$ by $12^\circ$. Find the degree measure of $\angle BAG$.

[asy] pair A,B,C,D,E,F,G,H,I,O; O=(0,0); C=dir(90); B=dir(70); A=dir(50); D=dir(110); E=dir(130); draw(arc(O,1,50,130)); real x=2*sin(20*pi/180); F=x*dir(228)+C; G=x*dir(256)+C; H=x*dir(284)+C; I=x*dir(312)+C; draw(arc(C,x,200,340)); label("$A$",A,dir(0)); label("$B$",B,dir(75)); label("$C$",C,dir(90)); label("$D$",D,dir(105)); label("$E$",E,dir(180)); label("$F$",F,dir(225)); label("$G$",G,dir(260)); label("$H$",H,dir(280)); label("$I$",I,dir(315)); [/asy]

Solution 1

Let $O$ be the center of the circle with $ABCDE$ on it.

Let $x$ be the degree measurement of $\overarc{ED}=\overarc{DC}=\overarc{CB}=\overarc{BA}$ in circle $O$

and $y$ be the degree measurement of $\overarc{EF}=\overarc{FG}=\overarc{GH}=\overarc{HI}=\overarc{IA}$ in circle $C$.

$\angle ECA$ is, therefore, $5y$ by way of circle $C$ and \[\frac{360-4x}{2}=180-2x\] by way of circle $O$. $\angle ABD$ is $180 - \frac{3x}{2}$ by way of circle $O$, and \[\angle AHG = 180 - \frac{3y}{2}\] by way of circle $C$.

This means that:

\[180-\frac{3x}{2}=180-\frac{3y}{2}+12\]

which when simplified yields \[\frac{3x}{2}+12=\frac{3y}{2}\] or \[x+8=y\] Since: \[5y=180-2x\] and \[5x+40=180-2x\] So: \[7x=140\Longleftrightarrow x=20\] \[y=28\] $\angle BAG$ is equal to $\angle BAE$ + $\angle EAG$, which equates to $\frac{3x}{2} + y$. Plugging in yields $30+28$, or $\boxed{058}$.

Solution 2

Let $m$ be the degree measurement of $\angle GCH$. Since $G,H$ lie on a circle with center $C$, $\angle GHC=\frac{180-m}{2}=90-\frac{m}{2}$.

Since $\angle ACH=2 \angle GCH=2m$, $\angle AHC=\frac{180-2m}{2}=90-m$. Adding $\angle GHC$ and $\angle AHC$ gives $\angle AHG=180-\frac{3m}{2}$, and $\angle ABD=\angle AHG+12=192-\frac{3m}{2}$. Since $AE$ is parallel to $BD$, $\angle DBA=180-\angle ABD=\frac{3m}{2}-12=$$\overarc{BE}$.

We are given that $A,B,C,D,E$ are evenly distributed on a circle. Hence,

$\overarc{ED}=\overarc{DC}=\overarc{CB}=\overarc{BA}$$=\frac{\angle DBA}{3}=\frac{m}{2}-4$

Here comes the key: Draw a line through $C$ parallel to $AE$, and select a point $X$ to the right of point $C$.

$\angle ACX$ = $\overarc{AB}$ + $\overarc{BC}$ = $m-8$.

Let the midpoint of $\overline{HG}$ be $Y$, then $\angle YCX=\angle ACX+\angle ACY=(m-8)+\frac{5m}{2}=90$. Solving gives $m=28$

The rest of the solution proceeds as in solution 1, which gives $\boxed{058}$


Solution 3

2015 AIME I 6.png

Let $\angle GAH = \varphi \implies \overset{\Large\frown} {GH} = 2\varphi \implies$ \[\overset{\Large\frown} {EF} = \overset{\Large\frown} {FG} = \overset{\Large\frown} {HI} = \overset{\Large\frown} {IA} = 2\varphi \implies\] \[\angle AGH = 2\varphi, \angle ACE = 10 \varphi.\]

\[BD||GH \implies \angle AJB = \angle AGH = 2 \varphi.\] \[\triangle AHG: \hspace{10mm} \angle AHG = \beta = 180^\circ – 3 \varphi.\] $\hspace{10mm} \triangle ABJ: \hspace{10mm} \angle BAG + \angle ABD = \alpha + \gamma = 180^\circ + 2 \varphi.$

Let arc $\overset{\Large\frown} {AB} = 2\psi \implies$

$\angle ACE = \frac {360^\circ – 8 \psi}{2}= 180^\circ – 4 \psi, \angle ABD = \gamma =\frac {360^\circ – 6 \psi}{2} =180^\circ – 3 \psi.$ $\gamma – \beta = 3(\varphi – \psi) = 12^\circ \implies \psi = \varphi – 4^\circ \implies 10 \varphi = 180^\circ – 4(\varphi – 4^\circ) \implies 14 \varphi = 196^\circ \implies \varphi = 14^\circ.$

Therefore $\gamma = 180^\circ – 3 \cdot (14^\circ – 4^\circ) = 150^\circ \implies \alpha = 180^\circ + 2 \cdot 14^\circ – 150^\circ = \boxed{\textbf{058}}.$


Video Solution

https://youtu.be/IuwkX2Dv25s

~MathProblemSolvingSkills.com


See Also

2015 AIME I (Problems • Answer Key • Resources)
Preceded by
Problem 5 		Followed by
Problem 7
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2015_AIME_I_Problems/Problem_6&oldid=195958"