Difference between revisions of "2015 AIME I Problems/Problem 11"

Latest revision as of 16:43, 27 September 2023

Problem

Triangle $ABC$ has positive integer side lengths with $AB=AC$ . Let $I$ be the intersection of the bisectors of $\angle B$ and $\angle C$ . Suppose $BI=8$ . Find the smallest possible perimeter of $\triangle ABC$ .

Solution 1

Let $D$ be the midpoint of $\overline{BC}$ . Then by SAS Congruence, $\triangle ABD \cong \triangle ACD$ , so $\angle ADB = \angle ADC = 90^o$ .

Now let $BD=y$ , $AB=x$ , and $\angle IBD = \dfrac{\angle ABD}{2} = \theta$ .

Then $\mathrm{cos}{(\theta)} = \dfrac{y}{8}$

and $\mathrm{cos}{(2\theta)} = \dfrac{y}{x} = 2\mathrm{cos^2}{(\theta)} - 1 = \dfrac{y^2-32}{32}$ .

Cross-multiplying yields $32y = x(y^2-32)$ .

Since $x,y>0$ , $y^2-32$ must be positive, so $y > 5.5$ .

Additionally, since $\triangle IBD$ has hypotenuse $\overline{IB}$ of length $8$ , $BD=y < 8$ .

Therefore, given that $BC=2y$ is an integer, the only possible values for $y$ are $6$ , $6.5$ , $7$ , and $7.5$ .

However, only one of these values, $y=6$ , yields an integral value for $AB=x$ , so we conclude that $y=6$ and $x=\dfrac{32(6)}{(6)^2-32}=48$ .

Thus the perimeter of $\triangle ABC$ must be $2(x+y) = \boxed{108}$ .

Solution 2 (No Trig)

Let $AB=x$ and the foot of the altitude from $A$ to $BC$ be point $E$ and $BE=y$ . Since ABC is isosceles, $I$ is on $AE$ . By Pythagorean Theorem, $AE=\sqrt{x^2-y^2}$ . Let $IE=a$ and $IA=b$ . By Angle Bisector theorem, $\frac{y}{a}=\frac{x}{b}$ . Also, $a+b=\sqrt{x^2-y^2}$ . Solving for $a$ , we get $a=\frac{\sqrt{x^2-y^2}}{1+\frac{x}{y}}$ . Then, using Pythagorean Theorem on $\triangle BEI$ we have $y^2+\left(\frac{\sqrt{x^2-y^2}}{1+\frac{x}{y}}\right)^2=8^2=64$ . Simplifying, we have $y^2+y^2\frac{x^2-y^2}{(x+y)^2}=64$ . Factoring out the $y^2$ , we have $y^2\left(1+\frac{x^2-y^2}{(x+y)^2}\right)=64$ . Adding 1 to the fraction and simplifying, we have $\frac{y^2x(x+y)}{(x+y)^2}=32$ . Crossing out the $x+y$ , and solving for $x$ yields $32y = x(y^2-32)$ . Then, we continue as Solution 1 does.

Solution 3

Let $AB=x$ , call the midpoint of $BC$ point $E$ , call the point where the incircle meets $AB$ point $D$ ,

and let $BE=y$ . We are looking for the minimum value of $2(x+y)$ . $AE$ is an altitude because the triangle

is isosceles. By Pythagoras on $BEI$ , the inradius is $\sqrt{64-y^2}$ and by Pythagoras on $ABE$ , $AE$ is

$\sqrt{x^2-y^2}$ . By equal tangents, $BE=BD=y$ , so $AD=x-y$ . Since $ID$ is an inradius, $ID=IE$ and using pythagoras on $ADI$ yields $AI=$ $\sqrt{x^2-2xy+64}$ . $ADI$ is similar to $AEB$ by $AA$ , so we

can write $\frac{x-y}{\sqrt{x^2-2xy+64}}=\frac{\sqrt{x^2-y^2}}{x}$ . Simplifying, $\frac{x}{\sqrt{x^2-2xy+64}}=\sqrt{\frac{x+y}{x-y}}$ .

Squaring, subtracting 1 from both sides, and multiplying everything out, we get $yx^2-2xy^2+64y=yx^2 -32x+32y-xy^2$ , which turns into $32y=x(y^2-32)$ . Finish as in Solution 1.

Solution 4

Angle bisectors motivate trig bash. Define angle $IBC = x$ . Foot of perpendicular from $I$ to $BC$ is point $P$ . $\overline{BC} = 2\overline{BP} = 2(8\cos(x)) = N$ , where $N$ is an integer. Thus, $\cos(x) = \frac{N}{16}$ . Via double angle, we calculate $\overline{AB}$ to be $\frac{8\cos(x)}{2\cos(x)^2 - 1} = \frac{64N}{N^2 - 128}$ . This is to be an integer. We can bound $N$ now, as $N > 11$ to avoid negative values and $N < 16$ due to triangle inequality. Testing, $N = 12$ works, giving $\overline{AB} = 48, \overline{BC} = 12$ . Our answer is $2 * 48 + 12 = \boxed{108}$ . - whatRthose

Solution 5

Let $M$ be midpoint $BC, BM = x, AB = y, \angle IBM = \alpha.$

$BI$ is the bisector of $\angle ABM$ in $\triangle ABM.$ $BI = \frac {2 xy \cos \alpha}{x+y} = 8, \cos \alpha = \frac {x}{8} \implies \frac {x^2 y}{x+y} = 32.$ $y = \frac {32 x} {x^2 - 32}.$ $BC = 2x$ is integer, $5.5^2 < 32 \implies x \ge 6.$ $BM < BI \implies x =\{ 6, 6.5, 7, 7.5 \}.$

If $x > 6$ then $y$ is not integer. $x = 6 \implies y = 48 \implies 2(x+y) = \boxed{\textbf{108}}.$ vladimir.shelomovskii@gmail.com, vvsss

Video Solution

https://youtu.be/R8kvayz7Rtw?si=hFg4yGZO4dxyxAuG

~MathProblemSolvingSkills.com

@@ Line 1: / Line 1: @@
 ==Problem==
 Triangle <math>ABC</math> has positive integer side lengths with <math>AB=AC</math>. Let <math>I</math> be the intersection of the bisectors of <math>\angle B</math> and <math>\angle C</math>. Suppose <math>BI=8</math>. Find the smallest possible perimeter of <math>\triangle ABC</math>.
+==Solution 1==
+Let <math>D</math> be the midpoint of <math>\overline{BC}</math>. Then by SAS Congruence, <math>\triangle ABD \cong \triangle ACD</math>, so <math>\angle ADB = \angle ADC = 90^o</math>.
+Now let <math>BD=y</math>, <math>AB=x</math>, and <math>\angle IBD = \dfrac{\angle ABD}{2} = \theta</math>.
+Then <math>\mathrm{cos}{(\theta)} = \dfrac{y}{8}</math>
+and <math>\mathrm{cos}{(2\theta)} = \dfrac{y}{x} = 2\mathrm{cos^2}{(\theta)} - 1 = \dfrac{y^2-32}{32}</math>.
+Cross-multiplying yields <math>32y = x(y^2-32)</math>.
+Since <math>x,y>0</math>, <math>y^2-32</math> must be positive, so <math>y > 5.5</math>.
+Additionally, since <math>\triangle IBD</math> has hypotenuse <math>\overline{IB}</math> of length <math>8</math>, <math>BD=y < 8</math>.
+Therefore, given that <math>BC=2y</math> is an integer, the only possible values for <math>y</math> are <math>6</math>, <math>6.5</math>, <math>7</math>, and <math>7.5</math>.
+However, only one of these values, <math>y=6</math>, yields an integral value for <math>AB=x</math>, so we conclude that <math>y=6</math> and <math>x=\dfrac{32(6)}{(6)^2-32}=48</math>.
+Thus the perimeter of <math>\triangle ABC</math> must be <math>2(x+y) = \boxed{108}</math>.
+==Solution 2 (No Trig)==
+Let <math>AB=x</math> and the foot of the altitude from <math>A</math> to <math>BC</math> be point <math>E</math> and <math>BE=y</math>. Since ABC is isosceles, <math>I</math> is on <math>AE</math>. By Pythagorean Theorem, <math>AE=\sqrt{x^2-y^2}</math>. Let <math>IE=a</math> and <math>IA=b</math>. By Angle Bisector theorem, <math>\frac{y}{a}=\frac{x}{b}</math>. Also, <math>a+b=\sqrt{x^2-y^2}</math>. Solving for <math>a</math>, we get <math>a=\frac{\sqrt{x^2-y^2}}{1+\frac{x}{y}}</math>. Then, using Pythagorean Theorem on <math>\triangle BEI</math> we have <math>y^2+\left(\frac{\sqrt{x^2-y^2}}{1+\frac{x}{y}}\right)^2=8^2=64</math>. Simplifying, we have <math>y^2+y^2\frac{x^2-y^2}{(x+y)^2}=64</math>. Factoring out the <math>y^2</math>, we have <math>y^2\left(1+\frac{x^2-y^2}{(x+y)^2}\right)=64</math>. Adding 1 to the fraction and simplifying, we have <math>\frac{y^2x(x+y)}{(x+y)^2}=32</math>. Crossing out the <math>x+y</math>, and solving for <math>x</math> yields <math>32y = x(y^2-32)</math>. Then, we continue as Solution 1 does.
+==Solution 3==
+Let <math>AB=x</math>, call the midpoint of <math>BC</math> point <math>E</math>, call the point where the incircle meets <math>AB</math> point <math>D</math>,
+and let <math>BE=y</math>. We are looking for the minimum value of <math>2(x+y)</math>. <math>AE</math> is an altitude because the triangle
+is isosceles. By Pythagoras on <math>BEI</math>, the inradius is <math>\sqrt{64-y^2}</math> and by Pythagoras on <math>ABE</math>, <math>AE</math> is
+<math>\sqrt{x^2-y^2}</math>. By equal tangents, <math>BE=BD=y</math>, so <math>AD=x-y</math>. Since <math>ID</math> is an inradius, <math>ID=IE</math> and
+using pythagoras on <math>ADI</math> yields <math>AI=</math><math>\sqrt{x^2-2xy+64}</math>. <math>ADI</math> is similar to <math>AEB</math> by <math>AA</math>, so we
+can write <math>\frac{x-y}{\sqrt{x^2-2xy+64}}=\frac{\sqrt{x^2-y^2}}{x}</math>. Simplifying, <math>\frac{x}{\sqrt{x^2-2xy+64}}=\sqrt{\frac{x+y}{x-y}}</math>.
+Squaring, subtracting 1 from both sides, and multiplying everything out, we get <math>yx^2-2xy^2+64y=yx^2 -32x+32y-xy^2</math>, which turns into <math>32y=x(y^2-32)</math>. Finish as in Solution 1.
+==Solution 4==
+Angle bisectors motivate trig bash.
+Define angle <math>IBC = x</math>. Foot of perpendicular from <math>I</math> to <math>BC</math> is point <math>P</math>.
+<math>\overline{BC} = 2\overline{BP} = 2(8\cos(x)) = N</math>, where <math>N</math> is an integer. Thus, <math>\cos(x) = \frac{N}{16}</math>. Via double angle, we calculate <math>\overline{AB}</math> to be <math>\frac{8\cos(x)}{2\cos(x)^2 - 1} = \frac{64N}{N^2 - 128}</math>. This is to be an integer.  We can bound <math>N</math> now, as <math>N > 11</math> to avoid negative values and <math>N < 16</math> due to triangle inequality. Testing, <math>N = 12</math> works, giving <math>\overline{AB} = 48, \overline{BC} = 12</math>.
+Our answer is <math>2 * 48 + 12 = \boxed{108}</math>.
+- whatRthose
+==Solution 5==
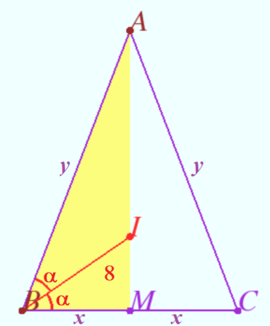
+[[File:2015 AIME I 11.png|270px|right]]
+Let <math>M</math> be midpoint <math>BC, BM = x, AB = y, \angle IBM = \alpha.</math>
+<math>BI</math> is the bisector of <math>\angle ABM</math> in <math>\triangle ABM.</math>
+<math>BI = \frac {2 xy \cos \alpha}{x+y} = 8, \cos \alpha = \frac {x}{8} \implies \frac {x^2 y}{x+y} = 32.</math>
+<cmath>y = \frac {32 x} {x^2 - 32}.</cmath>
+<math>BC = 2x</math> is integer, <math>5.5^2 < 32 \implies x \ge 6.</math>
+<math>BM < BI \implies x =\{ 6, 6.5, 7, 7.5 \}.</math>
+If <math>x > 6</math> then <math>y</math> is not integer.
+<cmath>x = 6 \implies y = 48 \implies 2(x+y) =  \boxed{\textbf{108}}.</cmath>
+'''vladimir.shelomovskii@gmail.com, vvsss'''
+==Video Solution==
+https://youtu.be/R8kvayz7Rtw?si=hFg4yGZO4dxyxAuG
+~MathProblemSolvingSkills.com
 ==See Also==
 {{AIME box|year=2015|n=I|num-b=10|num-a=12}}
 {{MAA Notice}}
+[[Category: Intermediate Geometry Problems]]

2015 AIME I (Problems • Answer Key • Resources)
Preceded by Problem 10	Followed by Problem 12
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search