Difference between revisions of "2016 AIME II Problems/Problem 14"
Mathgeek2006 (talk | contribs) m |
Ninjaforce (talk | contribs) |
||
| (29 intermediate revisions by 16 users not shown) | |||
| Line 1: | Line 1: | ||
| + | ==Problem== | ||
Equilateral <math>\triangle ABC</math> has side length <math>600</math>. Points <math>P</math> and <math>Q</math> lie outside the plane of <math>\triangle ABC</math> and are on opposite sides of the plane. Furthermore, <math>PA=PB=PC</math>, and <math>QA=QB=QC</math>, and the planes of <math>\triangle PAB</math> and <math>\triangle QAB</math> form a <math>120^{\circ}</math> dihedral angle (the angle between the two planes). There is a point <math>O</math> whose distance from each of <math>A,B,C,P,</math> and <math>Q</math> is <math>d</math>. Find <math>d</math>. | Equilateral <math>\triangle ABC</math> has side length <math>600</math>. Points <math>P</math> and <math>Q</math> lie outside the plane of <math>\triangle ABC</math> and are on opposite sides of the plane. Furthermore, <math>PA=PB=PC</math>, and <math>QA=QB=QC</math>, and the planes of <math>\triangle PAB</math> and <math>\triangle QAB</math> form a <math>120^{\circ}</math> dihedral angle (the angle between the two planes). There is a point <math>O</math> whose distance from each of <math>A,B,C,P,</math> and <math>Q</math> is <math>d</math>. Find <math>d</math>. | ||
| − | ==Solution== | + | ==Solution 1== |
| − | The inradius of <math>\triangle ABC</math> is <math>100\sqrt 3</math> and the circumradius is <math>200 \sqrt 3</math>. Now, consider the line perpendicular to plane <math>ABC</math> through the circumcenter of <math>\triangle ABC</math>. Note that <math>P,Q,O</math> must lie on that line to be equidistant from each of the triangle's vertices. Also, note that since <math>P, Q, O</math> are collinear, and <math>OP=OQ</math>, we must have <math>O</math> is the midpoint of <math>PQ</math>. Now, Let <math>K</math> be the circumcenter of <math>\triangle ABC</math>, and <math>L</math> be the foot of the altitude from <math>A</math> to <math>BC</math>. We must have <math>\tan(\angle KLP+ \angle QLK)= \tan(120^{\circ})</math>. Setting <math>KP=x</math> and <math>KQ=y</math>, assuming WLOG <math>x>y</math>, we must have <math> | + | The inradius of <math>\triangle ABC</math> is <math>100\sqrt 3</math> and the circumradius is <math>200 \sqrt 3</math>. Now, consider the line perpendicular to plane <math>ABC</math> through the circumcenter of <math>\triangle ABC</math>. Note that <math>P,Q,O</math> must lie on that line to be equidistant from each of the triangle's vertices. Also, note that since <math>P, Q, O</math> are collinear, and <math>OP=OQ</math>, we must have <math>O</math> is the midpoint of <math>PQ</math>. Now, Let <math>K</math> be the circumcenter of <math>\triangle ABC</math>, and <math>L</math> be the foot of the altitude from <math>A</math> to <math>BC</math>. We must have <math>\tan(\angle KLP+ \angle QLK)= \tan(120^{\circ})</math>. Setting <math>KP=x</math> and <math>KQ=y</math>, assuming WLOG <math>x>y</math>, we must have <math>\tan(120^{\circ})=-\sqrt{3}=\dfrac{\dfrac{x+y}{100 \sqrt{3}}}{\dfrac{30000-xy}{30000}}</math>. Therefore, we must have <math>100(x+y)=xy-30000</math>. Also, we must have <math>\left(\dfrac{x+y}{2}\right)^{2}=\left(\dfrac{x-y}{2}\right)^{2}+120000</math> by the Pythagorean theorem, so we have <math>xy=120000</math>, so substituting into the other equation we have <math>90000=100(x+y)</math>, or <math>x+y=900</math>. Since we want <math>\dfrac{x+y}{2}</math>, the desired answer is <math>\boxed{450}</math>. |
| − | Solution by | + | ==Solution 2 (Short & Simple)== |
| + | Draw a good diagram. Draw <math>CH</math> as an altitude of the triangle. Scale everything down by a factor of <math>100\sqrt{3}</math>, so that <math>AB=2\sqrt{3}</math>. Finally, call the center of the triangle U. Draw a cross-section of the triangle via line <math>CH</math>, which of course includes <math>P, Q</math>. From there, we can call <math>OU=h</math>. There are two crucial equations we can thus generate. WLOG set <math>PU<QU</math>, then we call <math>PU=d-h, QU=d+h</math>. First equation: using the Pythagorean Theorem on <math>\triangle UOB</math>, <math>h^2+2^2=d^2</math>. Next, using the tangent addition formula on angles <math>\angle PHU, \angle UHQ</math> we see that after simplifying <math>-d^2+h^2=-4, 2d=3\sqrt{3}</math> in the numerator, so <math>d=\frac{3\sqrt{3}}{2}</math>. Multiply back the scalar and you get <math>\boxed{450}</math>. Not that hard, was it? | ||
| + | |||
| + | ==Solution 3== | ||
| + | To make numbers more feasible, we'll scale everything down by a factor of <math>100</math> so that <math>\overline{AB}=\overline{BC}=\overline{AC}=6</math>. We should also note that <math>P</math> and <math>Q</math> must lie on the line that is perpendicular to the plane of <math>ABC</math> and also passes through the circumcenter of <math>ABC</math> (due to <math>P</math> and <math>Q</math> being equidistant from <math>A</math>, <math>B</math>, <math>C</math>), let <math>D</math> be the altitude from <math>C</math> to <math>AB</math>. We can draw a vertical cross-section of the figure then: <asy>pair C, D, I, P, Q, O; D=(0,0); C=(5.196152,0); P=(1.732051,7.37228); I=(1.732051,0); Q=(1.732051,-1.62772); O=(1.732051,2.87228); draw(C--Q--D--P--cycle); draw(C--D, dashed); draw(P--Q, dotted); draw(O--C, dotted); label("$C$", C, E); label("$D$", D, W); label("$I$", I, NW); label("$P$", P, N); label("$Q$", Q, S); label("$O$", O, SW); dot(O); dot(I);</asy> We let <math>\angle PDI=\alpha</math> so <math>\angle QDI=120^{\circ}-\alpha</math>, also note that <math>\overline{PO}=\overline{QO}=\overline{CO}=d</math>. Because <math>I</math> is the centroid of <math>ABC</math>, we know that ratio of <math>\overline{CI}</math> to <math>\overline{DI}</math> is <math>2:1</math>. Since we've scaled the figure down, the length of <math>CD</math> is <math>3\sqrt{3}</math>, from this it's easy to know that <math>\overline{CI}=2\sqrt{3}</math> and <math>\overline{DI}=\sqrt{3}</math>. The following two equations arise: <cmath> | ||
| + | -fatant | ||
| + | |||
| + | ==Solution 4== | ||
| + | |||
| + | We use the diagram from solution 3. From basic angle chasing, | ||
| + | <cmath>180=\angle{QOC}+\angle{CO}P=2\angle{OCP}+2\angle{OCQ}=2\angle{QCP}</cmath> | ||
| + | so triangle QCP is a right triangle. This means that triangles <math>CQI</math> and <math>CPI</math> are similar. If we let <math>\angle{IDQ}=x</math> and <math>\angle{PDI}=y</math>, then we know <math>x+y=120</math> and <cmath>\frac{PG}{GC}=\frac{GC}{GQ}\Rightarrow\frac{100\sqrt{3}\tan{y}}{200\sqrt{3}}=\frac{200\sqrt{3}}{100\sqrt{3}\tan{x}}\Rightarrow\tan{x}\tan{y}=4</cmath> We also know that <cmath>PQ=2d=100\sqrt{3}(\tan{x}+\tan{y})</cmath> <cmath>d=50\sqrt{3}(\tan{x}+\tan{y})</cmath> <cmath>\frac{d}{1-\tan{x}\tan{y}}=50\sqrt{3}\cdot\frac{\tan{x}+\tan{y}}{1-\tan{x}\tan{y}}</cmath> <cmath>\frac{d}{-3}=50\sqrt{3}\tan{(x+y)}</cmath> <cmath>d=-150\sqrt{3}\tan{120}=-150\sqrt{3}(-\sqrt{3})=\boxed{450}</cmath> | ||
| + | |||
| + | -EZmath2006 | ||
| + | |||
| + | ==Solution 5== | ||
| + | |||
| + | We use the diagram from solution 3. | ||
| + | |||
| + | Let <math>BP = a</math> and <math>BQ = b</math>. Then, by Stewart's on <math>BPQ</math>, we find | ||
| + | <cmath>2x^3 + 2x^3 = a^2x + b^2x \implies a^2 + b^2 = 4x^2.</cmath> | ||
| + | |||
| + | The altitude from <math>P</math> to <math>ABC</math> is <math>\sqrt{a^2 - (200\sqrt{3})^2}</math> so | ||
| + | <cmath>PQ = 2x = \sqrt{a^2 - (200\sqrt{3})^2} + \sqrt{b^2 - (200\sqrt{3})^2}.</cmath> | ||
| + | |||
| + | Furthermore, the altitude from <math>P</math> to <math>AB</math> is <math>\sqrt{a^2 - 300^2}</math>, so, by LoC and the dihedral condition, | ||
| + | <cmath>a^2 - 300^2 + b^2 - 300^2 + \sqrt{a^2 - 300^2}\sqrt{b^2-300^2} = 4x^2.</cmath> | ||
| + | |||
| + | Squaring the equation for <math>PQ</math> and substituting <math>a^2 + b^2 = 4x^2</math> yields | ||
| + | <cmath>2\sqrt{a^2 - (200\sqrt{3})^2}\sqrt{b^2 - (200\sqrt{3})^2} = 6\cdot 200^2.</cmath> | ||
| + | |||
| + | Substituting <math>a^2 + b^2 = 4x^2</math> into the other equation, | ||
| + | <cmath>\sqrt{a^2 - 300^2}\sqrt{b^2-300^2} = 2\cdot 300^2.</cmath> | ||
| + | |||
| + | Squaring both of these gives | ||
| + | <cmath>a^2b^2-3\cdot 200^2(a^2 + b^2) + 9\cdot 200^4 = 9\cdot 200^4</cmath> | ||
| + | <cmath>a^2b^2 - 300^2(a^2+b^2) + 300^4 = 4\cdot 300^4.</cmath> | ||
| + | |||
| + | Substituting <math>a^2 + b^2 = 4x^2</math> and solving for <math>x</math> gives <math>\boxed{450}</math>, as desired. | ||
| + | |||
| + | -mathtiger6 | ||
| + | |||
| + | ==Solution 6 (Geometry)== | ||
| + | [[File:2016 AIME II 14.png|400px|right]] | ||
| + | [[File:2016 AIME II 14a.png|400px|right]] | ||
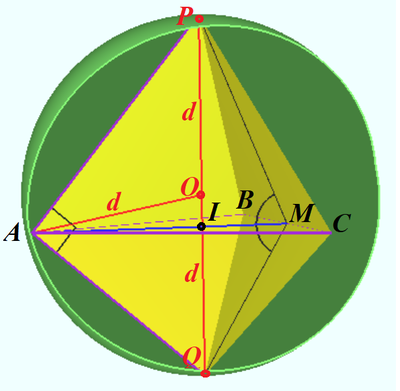
| + | Let <math>AB = a, M</math> be midpoint <math>BC, I</math> be the center of equilateral <math>\triangle ABC,</math> | ||
| + | <math>IM = b = \frac {a}{2\sqrt{3}}, O</math> be the center of sphere <math>ABCPQ.</math> | ||
| + | Then <cmath>AI = 2b, AO = BO = PO =QO = d.</cmath> | ||
| + | <cmath>QA=QB=QC,PA=PB=PC \implies</cmath> | ||
| + | <cmath>POIQ\perp ABC, \angle PMQ = 120^\circ.</cmath> | ||
| + | (See upper diagram). | ||
| + | |||
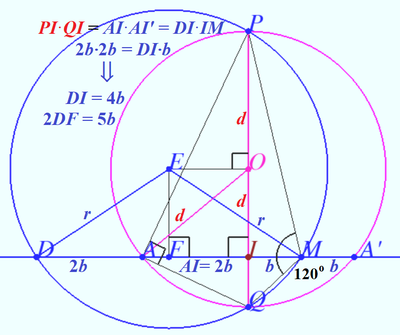
| + | We construct the circle PQMD, use the formulas for intersecting chords and get | ||
| + | <cmath>DI = 5b, FI = EO = \frac{3b}{2}</cmath> | ||
| + | <cmath>\implies FM = \frac{5b}{2}.</cmath> | ||
| + | (See lower diagram). | ||
| + | |||
| + | We apply the Law of Sine to <math>\triangle PMQ</math> and get | ||
| + | <cmath>2EM \sin 120^\circ =PQ</cmath> | ||
| + | <cmath>\implies r \sqrt{3} = 2d</cmath> | ||
| + | <cmath>\implies 3r^2 = 4d^2.</cmath> | ||
| + | We apply the Pythagorean Law on <math>\triangle AOI</math> and <math>\triangle EFM</math> and get | ||
| + | <cmath>d^2 = 4b^2 + OI^2, r^2 = \frac {25b^2}{4} + EF^2 \implies</cmath> | ||
| + | <cmath>r = 3b\implies d = \frac {3a}{2} = \boxed {450}.</cmath> | ||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==Solution 7== | ||
| + | Let <math>M</math> be the midpoint of <math>\overline{AB}</math> and <math>X</math> the center of <math>\triangle ABC</math>. Then <cmath>P, O, Q, M, X, C</cmath> all lie in the same vertical plane. We can make the following observations: | ||
| + | * The equilateral triangle has side length <math>600</math>, so <math>MC=300\sqrt{3}</math> and <math>X</math> divides <math>MC</math> so that <math>MX=100\sqrt{3}</math> and <math>XC=200\sqrt{3}</math>; | ||
| + | * <math>O</math> is the midpoint of <math>PQ</math> since <math>O</math> is equidistant from <math>A, B, C, P, Q</math> – it is also the circumcenter of <math>\triangle PCQ</math>; | ||
| + | * <math>\angle PMQ=120^{\circ}</math>, the dihedral angle. | ||
| + | |||
| + | To make calculations easier, we will denote <math>100\sqrt{3}=m</math>, so that <math>MX=m</math> and <math>XC=2m</math>. | ||
| + | |||
| + | <asy> | ||
| + | unitsize(20); | ||
| + | pair P = (0, 12); | ||
| + | pair Q = (0, -3); | ||
| + | pair O = (P+Q)/2; | ||
| + | pair M = (-3, 0); | ||
| + | pair X = (0, 0); | ||
| + | pair C = (6, 0); | ||
| + | draw(P--O--Q); | ||
| + | draw(M--X--C); | ||
| + | draw(P--M--Q, blue); | ||
| + | draw(Q--C--P); | ||
| + | draw(circle((0, 4.5), 7.5)); | ||
| + | label("$P$", P, N); | ||
| + | label("$Q$", Q, S); | ||
| + | label("$O$", O, E); | ||
| + | dot(O); | ||
| + | label("$M$", M, W); | ||
| + | label("$X$", X, NE); | ||
| + | label("$C$", C, E); | ||
| + | label("$m$", (M+X)/2, N); | ||
| + | label("$2m$", (X+C)/2, N); | ||
| + | </asy> | ||
| + | |||
| + | Denote <math>PX=p</math> and <math>QX=q</math>, where the tangent addition formula on <math>\triangle PMQ</math> yields <cmath>\frac{\tan\measuredangle PMX+\tan\measuredangle QMX}{1-\tan\measuredangle PMX\tan\measuredangle QMX}=\tan(120^{\circ})=-\sqrt{3}.</cmath> Using <math>\tan\measuredangle PMX=\frac{p}{m}</math> and <math>\tan\measuredangle QMX=\frac{q}{m}</math>, we have <cmath>\frac{\frac{p}{m}+\frac{q}{m}}{1-\frac{p}{m}\cdot\frac{q}{m}}=-\sqrt{3}.</cmath> After multiplying both numerator and denominator by <math>m^{2}</math> we have <cmath>\frac{(p+q)m}{m^{2}-pq}=-\sqrt{3}.</cmath> But note that <math>pq=(2m)(2m)=4m^{2}</math> by power of a point at <math>X</math>, where we deduce by symmetry that <math>MM^{\prime}=MX=m</math> on the diagram below: <asy> | ||
| + | unitsize(20); | ||
| + | pair P = (0, 12); | ||
| + | pair Q = (0, -3); | ||
| + | pair O = (P+Q)/2; | ||
| + | pair M = (-3, 0); | ||
| + | pair Mprime = (-6, 0); | ||
| + | pair X = (0, 0); | ||
| + | pair C = (6, 0); | ||
| + | draw(P--O--Q); | ||
| + | draw(Mprime--M--X--C); | ||
| + | draw(P--M--Q, blue); | ||
| + | draw(Q--C--P); | ||
| + | draw(circle((0, 4.5), 7.5)); | ||
| + | label("$P$", P, N); | ||
| + | label("$Q$", Q, S); | ||
| + | label("$O$", O, E); | ||
| + | dot(O); | ||
| + | label("$M$", M, S); | ||
| + | label("$M^{\prime}$", Mprime, W); | ||
| + | label("$X$", X, SE); | ||
| + | label("$C$", C, E); | ||
| + | label("$m$", (Mprime+M)/2, N); | ||
| + | label("$m$", (M+X)/2, N); | ||
| + | label("$2m$", (X+C)/2, N); | ||
| + | </asy> | ||
| + | |||
| + | Thus <cmath> | ||
| + | |||
| + | ==Solution 8 (Law of Cosines)== | ||
| + | |||
| + | Let <math>Z</math> be the center of <math>\triangle ABC</math>. Let <math>A’</math> be the midpoint of <math>BC</math>. Let <math>ZA’ = c = 100\sqrt{3}</math> and <math>ZA = 2c = 200\sqrt{3}</math>. Let <math>PZ = a</math> and <math>QZ = b</math>. We will be working in the plane that contains the points: <math>A</math>, <math>P</math>, <math>A’</math>, <math>Q</math>, <math>O</math>, and <math>Z</math>. | ||
| + | |||
| + | Since <math>P</math>, <math>O</math>, and <math>Q</math> are collinear and <math>PO = QO = AO</math>, <math>\triangle PAQ</math> is a right triangle with <math>\angle PAQ = 90^{\circ}</math>. Since <math>AZ \perp PQ</math>, <math>(PZ)(QZ) = (AZ)^2 = ab = (2c)^2 = 120000</math>. | ||
| + | |||
| + | <math>PA’ = \sqrt{a^2 + c^2}</math>, <math>QA’ = \sqrt{b^2 + c^2}</math>, <math>PQ = a + b</math>, and <math>\angle PAQ = 120^{\circ}</math>. By Law of Cosines <cmath>(a + b)^2 = a^2 + b^2 + 2c^2 + \sqrt{a^2b^2 + a^2c^2 + b^2c^2 + c^4}</cmath>. Substituting <math>4c^2</math> for <math>ab</math> and simplifying, we get <cmath>6c = \sqrt{17c^2 + a^2 + b^2}</cmath>. Squaring and simplifying, we get <cmath>a^2 + b^2 = 19c^2 = 570000</cmath>. Adding <math>2ab = 8c^2</math> to both sides we get <math>PQ = a + b = 900</math>. Since <math>O</math> is the midpoint of <math>PQ</math>, <math>d = PO = \boxed{450}</math> | ||
| + | |||
| + | ~numerophile | ||
| + | |||
| + | ==Solution 9 (Coordinate Bash)== | ||
| + | |||
| + | Set <math>AB = s, M</math> as midpoint <math>BC, I</math> as the center of equilateral <math>\triangle ABC,</math> and by <math>30-60-90</math> triangle formulas, we know <math>IM = b = \frac {s}{2\sqrt{3}}, IA = IB = IC = \frac{s}{\sqrt{3}}</math>. | ||
| + | |||
| + | First note that <math>P</math> and <math>Q</math> are on the line perpendicular to plane <math>ABC</math> through the circumcenter of <math>\triangle ABC</math>. Then notice that point <math>O</math> is the midpoint of <math>PQ</math>, so it also lies on this axis. Then, we see that the position of <math>O</math> relative to the triangle fully determines the positions of both <math>P</math> and <math>Q</math>, so setting the coordinates of <math>O</math> as <math>(0,0,h)</math> where the origin is defined the circumcenter and <math>\triangle ABC</math> lies in the <math>xy</math>-plane, we get: <cmath> | ||
| + | |||
| + | Thus, the coordinates of <math>P</math> and <math>Q</math> are <math>(0,0,h\pm\sqrt{h^2+\frac{s^2}{3}})</math>. Now we make use of the angle condition. WLOG set the coordinates of <math>M</math> as <math>(\frac{s}{2\sqrt{3}},0,0)</math>. We know the angle between <math>PM</math> and <math>QM</math> is <math>120^{\circ}</math>, so after solving for the vectors, taking their dot product, equating it to <math>PM \cdot QM \cdot\cos{120^{\circ}}</math>, and <math>\textit{finally}</math> solving for <math>h</math> in terms of <math>s</math>, we get <cmath>\[ | ||
| + | h^2 = \frac{11}{48}s^2 \ | ||
| + | \implies OA^2 = h^2 + \frac{s^2}{3} = \frac{27}{48}s^2 \ | ||
| + | \implies OA = \frac{3}{4}s = \boxed{450} | ||
| + | \]</cmath> | ||
| + | |||
| + | |||
| + | (If someone feels like it, please feel free to fill in the rest of the details!) | ||
| + | |||
| + | ~ninjaforce | ||
| + | |||
| + | ==Video Solution by MOP 2024== | ||
| + | https://youtu.be/hyhIlsAR2hs | ||
| + | |||
| + | ~r00tsOfUnity | ||
== See also == | == See also == | ||
{{AIME box|year=2016|n=II|num-b=13|num-a=15}} | {{AIME box|year=2016|n=II|num-b=13|num-a=15}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
| + | [[Category:Intermediate Geometry Problems]] | ||
| + | [[Category:3D Geometry Problems]] | ||
Latest revision as of 18:39, 25 November 2024
Contents
[hide]Problem
Equilateral ![]() has side length
has side length ![]() . Points
. Points ![]() and
and ![]() lie outside the plane of
lie outside the plane of ![]() and are on opposite sides of the plane. Furthermore,
and are on opposite sides of the plane. Furthermore, ![]() , and
, and ![]() , and the planes of
, and the planes of ![]() and
and ![]() form a
form a ![]() dihedral angle (the angle between the two planes). There is a point
dihedral angle (the angle between the two planes). There is a point ![]() whose distance from each of
whose distance from each of ![]() and
and ![]() is
is ![]() . Find
. Find ![]() .
.
Solution 1
The inradius of ![]() is
is ![]() and the circumradius is
and the circumradius is ![]() . Now, consider the line perpendicular to plane
. Now, consider the line perpendicular to plane ![]() through the circumcenter of
through the circumcenter of ![]() . Note that
. Note that ![]() must lie on that line to be equidistant from each of the triangle's vertices. Also, note that since
must lie on that line to be equidistant from each of the triangle's vertices. Also, note that since ![]() are collinear, and
are collinear, and ![]() , we must have
, we must have ![]() is the midpoint of
is the midpoint of ![]() . Now, Let
. Now, Let ![]() be the circumcenter of
be the circumcenter of ![]() , and
, and ![]() be the foot of the altitude from
be the foot of the altitude from ![]() to
to ![]() . We must have
. We must have ![]() . Setting
. Setting ![]() and
and ![]() , assuming WLOG
, assuming WLOG ![]() , we must have
, we must have  . Therefore, we must have
. Therefore, we must have ![]() . Also, we must have
. Also, we must have ![]() by the Pythagorean theorem, so we have
by the Pythagorean theorem, so we have ![]() , so substituting into the other equation we have
, so substituting into the other equation we have ![]() , or
, or ![]() . Since we want
. Since we want ![]() , the desired answer is
, the desired answer is ![]() .
.
Solution 2 (Short & Simple)
Draw a good diagram. Draw ![]() as an altitude of the triangle. Scale everything down by a factor of
as an altitude of the triangle. Scale everything down by a factor of ![]() , so that
, so that ![]() . Finally, call the center of the triangle U. Draw a cross-section of the triangle via line
. Finally, call the center of the triangle U. Draw a cross-section of the triangle via line ![]() , which of course includes
, which of course includes ![]() . From there, we can call
. From there, we can call ![]() . There are two crucial equations we can thus generate. WLOG set
. There are two crucial equations we can thus generate. WLOG set ![]() , then we call
, then we call ![]() . First equation: using the Pythagorean Theorem on
. First equation: using the Pythagorean Theorem on ![]() ,
, ![]() . Next, using the tangent addition formula on angles
. Next, using the tangent addition formula on angles ![]() we see that after simplifying
we see that after simplifying ![]() in the numerator, so
in the numerator, so ![]() . Multiply back the scalar and you get
. Multiply back the scalar and you get ![]() . Not that hard, was it?
. Not that hard, was it?
Solution 3
To make numbers more feasible, we'll scale everything down by a factor of ![]() so that
so that ![]() . We should also note that
. We should also note that ![]() and
and ![]() must lie on the line that is perpendicular to the plane of
must lie on the line that is perpendicular to the plane of ![]() and also passes through the circumcenter of
and also passes through the circumcenter of ![]() (due to
(due to ![]() and
and ![]() being equidistant from
being equidistant from ![]() ,
, ![]() ,
, ![]() ), let
), let ![]() be the altitude from
be the altitude from ![]() to
to ![]() . We can draw a vertical cross-section of the figure then:
. We can draw a vertical cross-section of the figure then: ![[asy]pair C, D, I, P, Q, O; D=(0,0); C=(5.196152,0); P=(1.732051,7.37228); I=(1.732051,0); Q=(1.732051,-1.62772); O=(1.732051,2.87228); draw(C--Q--D--P--cycle); draw(C--D, dashed); draw(P--Q, dotted); draw(O--C, dotted); label("$C$", C, E); label("$D$", D, W); label("$I$", I, NW); label("$P$", P, N); label("$Q$", Q, S); label("$O$", O, SW); dot(O); dot(I);[/asy]](http://latex.artofproblemsolving.com/e/f/a/efaeb3adee97ec95aa69d4c1d7682595037fb1e8.png) We let
We let ![]() so
so ![]() , also note that
, also note that ![]() . Because
. Because ![]() is the centroid of
is the centroid of ![]() , we know that ratio of
, we know that ratio of ![]() to
to ![]() is
is ![]() . Since we've scaled the figure down, the length of
. Since we've scaled the figure down, the length of ![]() is
is ![]() , from this it's easy to know that
, from this it's easy to know that ![]() and
and ![]() . The following two equations arise:
. The following two equations arise:  Using trig identities for the tangent, we find that
Using trig identities for the tangent, we find that  Okay, now we can plug this into
Okay, now we can plug this into ![]() to get:
to get:  Notice that
Notice that ![]() only appears in the above system of equations in the form of
only appears in the above system of equations in the form of ![]() , we can set
, we can set ![]() for convenience since we really only care about
for convenience since we really only care about ![]() . Now we have
. Now we have  Looking at
Looking at ![]() , it's tempting to square it to get rid of the square-root so now we have:
, it's tempting to square it to get rid of the square-root so now we have: ![]() See the sneaky
See the sneaky ![]() in the above equation? That we means we can substitute it for
in the above equation? That we means we can substitute it for ![]() :
:  Use the quadratic formula, we find that
Use the quadratic formula, we find that ![]() - the two solutions were expected because
- the two solutions were expected because ![]() can be
can be ![]() or
or ![]() . We can plug this into
. We can plug this into ![]() :
:  I'll use
I'll use ![]() because both values should give the same answer for
because both values should give the same answer for ![]() .
.  Wait! Before you get excited, remember that we scaled the entire figure by
Wait! Before you get excited, remember that we scaled the entire figure by ![]() ?? That means that the answer is
?? That means that the answer is ![]() .
-fatant
.
-fatant
Solution 4
We use the diagram from solution 3. From basic angle chasing,
![]() so triangle QCP is a right triangle. This means that triangles
so triangle QCP is a right triangle. This means that triangles ![]() and
and ![]() are similar. If we let
are similar. If we let ![]() and
and ![]() , then we know
, then we know ![]() and
and ![]() We also know that
We also know that ![]()
![]()
![]()
![]()
![]()
-EZmath2006
Solution 5
We use the diagram from solution 3.
Let ![]() and
and ![]() . Then, by Stewart's on
. Then, by Stewart's on ![]() , we find
, we find
![]()
The altitude from ![]() to
to ![]() is
is ![]() so
so
![]()
Furthermore, the altitude from ![]() to
to ![]() is
is ![]() , so, by LoC and the dihedral condition,
, so, by LoC and the dihedral condition,
![]()
Squaring the equation for ![]() and substituting
and substituting ![]() yields
yields
![]()
Substituting ![]() into the other equation,
into the other equation,
![]()
Squaring both of these gives
![]()
![]()
Substituting ![]() and solving for
and solving for ![]() gives
gives ![]() , as desired.
, as desired.
-mathtiger6
Solution 6 (Geometry)
Let ![]() be midpoint
be midpoint ![]() be the center of equilateral
be the center of equilateral ![]()
![]() be the center of sphere
be the center of sphere ![]() Then
Then ![]()
![]()
![]() (See upper diagram).
(See upper diagram).
We construct the circle PQMD, use the formulas for intersecting chords and get
![]()
![]() (See lower diagram).
(See lower diagram).
We apply the Law of Sine to ![]() and get
and get
![]()
![]()
![]() We apply the Pythagorean Law on
We apply the Pythagorean Law on ![]() and
and ![]() and get
and get
![]()
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Solution 7
Let ![]() be the midpoint of
be the midpoint of ![]() and
and ![]() the center of
the center of ![]() . Then
. Then ![]() all lie in the same vertical plane. We can make the following observations:
all lie in the same vertical plane. We can make the following observations:
- The equilateral triangle has side length
 , so
, so  and
and  divides
divides  so that
so that  and
and  ;
;  is the midpoint of
is the midpoint of  since
since  is equidistant from
is equidistant from  – it is also the circumcenter of
– it is also the circumcenter of  ;
; , the dihedral angle.
, the dihedral angle.
To make calculations easier, we will denote ![]() , so that
, so that ![]() and
and ![]() .
.
![[asy] unitsize(20); pair P = (0, 12); pair Q = (0, -3); pair O = (P+Q)/2; pair M = (-3, 0); pair X = (0, 0); pair C = (6, 0); draw(P--O--Q); draw(M--X--C); draw(P--M--Q, blue); draw(Q--C--P); draw(circle((0, 4.5), 7.5)); label("$P$", P, N); label("$Q$", Q, S); label("$O$", O, E); dot(O); label("$M$", M, W); label("$X$", X, NE); label("$C$", C, E); label("$m$", (M+X)/2, N); label("$2m$", (X+C)/2, N); [/asy]](http://latex.artofproblemsolving.com/f/2/9/f2935430194dec37bb4ea5490f12c13f1538456f.png)
Denote ![]() and
and ![]() , where the tangent addition formula on
, where the tangent addition formula on ![]() yields
yields ![]() Using
Using ![]() and
and ![]() , we have
, we have ![]() After multiplying both numerator and denominator by
After multiplying both numerator and denominator by ![]() we have
we have ![]() But note that
But note that ![]() by power of a point at
by power of a point at ![]() , where we deduce by symmetry that
, where we deduce by symmetry that ![]() on the diagram below:
on the diagram below: ![[asy] unitsize(20); pair P = (0, 12); pair Q = (0, -3); pair O = (P+Q)/2; pair M = (-3, 0); pair Mprime = (-6, 0); pair X = (0, 0); pair C = (6, 0); draw(P--O--Q); draw(Mprime--M--X--C); draw(P--M--Q, blue); draw(Q--C--P); draw(circle((0, 4.5), 7.5)); label("$P$", P, N); label("$Q$", Q, S); label("$O$", O, E); dot(O); label("$M$", M, S); label("$M^{\prime}$", Mprime, W); label("$X$", X, SE); label("$C$", C, E); label("$m$", (Mprime+M)/2, N); label("$m$", (M+X)/2, N); label("$2m$", (X+C)/2, N); [/asy]](http://latex.artofproblemsolving.com/d/f/e/dfe4d44ec3cc7c7a40a2883bde36f27b40949bc1.png)
Thus  Earlier we assigned the variable
Earlier we assigned the variable ![]() to the length
to the length ![]() which implies
which implies ![]() . Thus the distance
. Thus the distance ![]() is equal to
is equal to ![]() .
.
Solution 8 (Law of Cosines)
Let ![]() be the center of
be the center of ![]() . Let
. Let ![]() be the midpoint of
be the midpoint of ![]() . Let
. Let ![]() and
and ![]() . Let
. Let ![]() and
and ![]() . We will be working in the plane that contains the points:
. We will be working in the plane that contains the points: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
Since ![]() ,
, ![]() , and
, and ![]() are collinear and
are collinear and ![]() ,
, ![]() is a right triangle with
is a right triangle with ![]() . Since
. Since ![]() ,
, ![]() .
.
![]() ,
, ![]() ,
, ![]() , and
, and ![]() . By Law of Cosines
. By Law of Cosines ![]() . Substituting
. Substituting ![]() for
for ![]() and simplifying, we get
and simplifying, we get ![]() . Squaring and simplifying, we get
. Squaring and simplifying, we get ![]() . Adding
. Adding ![]() to both sides we get
to both sides we get ![]() . Since
. Since ![]() is the midpoint of
is the midpoint of ![]() ,
, ![]()
~numerophile
Solution 9 (Coordinate Bash)
Set ![]() as midpoint
as midpoint ![]() as the center of equilateral
as the center of equilateral ![]() and by
and by ![]() triangle formulas, we know
triangle formulas, we know ![]() .
.
First note that ![]() and
and ![]() are on the line perpendicular to plane
are on the line perpendicular to plane ![]() through the circumcenter of
through the circumcenter of ![]() . Then notice that point
. Then notice that point ![]() is the midpoint of
is the midpoint of ![]() , so it also lies on this axis. Then, we see that the position of
, so it also lies on this axis. Then, we see that the position of ![]() relative to the triangle fully determines the positions of both
relative to the triangle fully determines the positions of both ![]() and
and ![]() , so setting the coordinates of
, so setting the coordinates of ![]() as
as ![]() where the origin is defined the circumcenter and
where the origin is defined the circumcenter and ![]() lies in the
lies in the ![]() -plane, we get:
-plane, we get: ![]()
Thus, the coordinates of ![]() and
and ![]() are
are ![]() . Now we make use of the angle condition. WLOG set the coordinates of
. Now we make use of the angle condition. WLOG set the coordinates of ![]() as
as ![]() . We know the angle between
. We know the angle between ![]() and
and ![]() is
is ![]() , so after solving for the vectors, taking their dot product, equating it to
, so after solving for the vectors, taking their dot product, equating it to ![]() , and
, and ![]() solving for
solving for ![]() in terms of
in terms of ![]() , we get
, we get ![]()
(If someone feels like it, please feel free to fill in the rest of the details!)
~ninjaforce
Video Solution by MOP 2024
~r00tsOfUnity
See also
| 2016 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 13 |
Followed by Problem 15 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()