Difference between revisions of "2016 AIME I Problems/Problem 15"
Theboombox77 (talk | contribs) (→Solution 3) |
|||
| (36 intermediate revisions by 15 users not shown) | |||
| Line 4: | Line 4: | ||
==Solution== | ==Solution== | ||
| + | Using the radical axis theorem, the lines <math>\overline{AD}, \overline{BC}, \overline{XY}</math> are all concurrent at one point, call it <math>F</math>. Now recall by Miquel's theorem in <math>\triangle FDC</math> the fact that quadrilaterals <math>DAXY</math> and <math>CBXY</math> are cyclic implies <math>FAXB</math> is cyclic as well. Denote <math>\omega_{3}\equiv(FAXB)</math> and <math>Z\equiv\ell\cap\overline{FXY}</math>. | ||
| − | ===Solution 1=== | + | Since point <math>Z</math> lies on the radical axis of <math>\omega_{1},\omega_{2}</math>, it has equal power with respect to both circles, thus <cmath>AZ^{2}=\text{Pow}_{\omega_{1}}(Z)=ZX\cdot ZY=\text{Pow}_{\omega_{2}}(Z)=ZB^{2}\implies AZ=ZB.</cmath> Also, notice that <cmath>AZ\cdot ZB=\text{Pow}_{\omega_{3}}(Z)=ZX\cdot ZF\implies ZY=ZF.</cmath> The diagonals of quadrilateral <math>FAYB</math> bisect each other at <math>Z</math>, so we conclude that <math>FAYB</math> is a parallelogram. Let <math>u:=ZX</math>, so that <math>ZY=ZF=u+47</math>. |
| + | |||
| + | Because <math>FAYB</math> is a parallelogram and quadrilaterals <math>DAXY, CBXY</math> are cyclic, <cmath>\angle DFX=\angle AFX=\angle BYX=\angle BCX=\angle FCX~~\text{and}~~\angle XDF=\angle XDA=\angle XYA=\angle XFB=\angle XFC</cmath> so we have the pair of similar triangles <math>\triangle DFX~\sim~\triangle FCX</math>. Thus <cmath>\dfrac{37}{2u+47}=\dfrac{2u+47}{67}\implies 2u+47=\sqrt{37\cdot 67}\implies u=\dfrac{1}{2}\left(\sqrt{37\cdot 67}-47\right).</cmath> Now compute <cmath>AB^{2}=4AZ^{2}=4\cdot ZX\cdot ZY=4u(u+47)=37\cdot 67-47^{2}=\textbf{270}.</cmath> | ||
| + | |||
| + | [[File:AIME 2016-I15 Geogebra Diagram.png|840px]] | ||
| + | |||
| + | ==Solution 1== | ||
| + | |||
| + | Let <math>Z = XY \cap AB</math>. By the radical axis theorem <math>AD, XY, BC</math> are concurrent, say at <math>P</math>. Moreover, <math>\triangle DXP \sim \triangle PXC</math> by simple angle chasing. Let <math>y = PX, x = XZ</math>. Then <cmath>\frac{y}{37} = \frac{67}{y} \qquad \implies \qquad y^2 = 37 \cdot 67.</cmath> Now, <math>AZ^2 = \tfrac 14 AB^2</math>, and by power of a point, <cmath>\begin{align*} | ||
| + | x(y-x) &= \tfrac 14 AB^2, \quad \text{and} \\ | ||
| + | x(47+x) &= \tfrac 14 AB^2 | ||
| + | \end{align*}</cmath> Solving, we get <cmath>\tfrac 14 AB^2 = \tfrac 12 (y-47)\cdot \tfrac 12 (y+47) \qquad \implies</cmath> | ||
| + | <cmath> \qquad AB ^ 2 = 37\cdot 67 - 47^2 = \boxed{270}</cmath> | ||
| + | |||
| + | ==Solution 2== | ||
By the Radical Axis Theorem <math>AD, XY, BC</math> concur at point <math>E</math>. | By the Radical Axis Theorem <math>AD, XY, BC</math> concur at point <math>E</math>. | ||
| Line 13: | Line 28: | ||
<cmath>XE^2 - XY^2 = (XE + XY)(XE - XY) = EY \cdot 2XS = 2SY \cdot 2SX = 4SA^2 = AB^2.</cmath>Hence <math>AB^2 = 37 \cdot 67 - 47^2 = \boxed{270}.</math> | <cmath>XE^2 - XY^2 = (XE + XY)(XE - XY) = EY \cdot 2XS = 2SY \cdot 2SX = 4SA^2 = AB^2.</cmath>Hence <math>AB^2 = 37 \cdot 67 - 47^2 = \boxed{270}.</math> | ||
| − | + | ==Solution 3== | |
First, we note that as <math>\triangle XDY</math> and <math>\triangle XYC</math> have bases along the same line, <math>\frac{[\triangle XDY]}{[\triangle XYC]}=\frac{DY}{YC}</math>. We can also find the ratio of their areas using the circumradius area formula. If <math>R_1</math> is the radius of <math>\omega_1</math> and if <math>R_2</math> is the radius of <math>\omega_2</math>, then | First, we note that as <math>\triangle XDY</math> and <math>\triangle XYC</math> have bases along the same line, <math>\frac{[\triangle XDY]}{[\triangle XYC]}=\frac{DY}{YC}</math>. We can also find the ratio of their areas using the circumradius area formula. If <math>R_1</math> is the radius of <math>\omega_1</math> and if <math>R_2</math> is the radius of <math>\omega_2</math>, then | ||
<cmath>\frac{[\triangle XDY]}{[\triangle XYC]}=\frac{(37\cdot 47\cdot DY)/(4R_1)}{(47\cdot 67\cdot YC)/(4R_2)}=\frac{37\cdot DY\cdot R_2}{67\cdot YC\cdot R_1}.</cmath> | <cmath>\frac{[\triangle XDY]}{[\triangle XYC]}=\frac{(37\cdot 47\cdot DY)/(4R_1)}{(47\cdot 67\cdot YC)/(4R_2)}=\frac{37\cdot DY\cdot R_2}{67\cdot YC\cdot R_1}.</cmath> | ||
| Line 65: | Line 80: | ||
<cmath>AB^2=30^2\cdot 37\cdot 67y^2=37\cdot 67-47^2=\boxed{270}.</cmath> | <cmath>AB^2=30^2\cdot 37\cdot 67y^2=37\cdot 67-47^2=\boxed{270}.</cmath> | ||
| − | ==Solution | + | ==Solution 4== |
<asy> | <asy> | ||
size(9cm); | size(9cm); | ||
| Line 96: | Line 111: | ||
<cmath>\theta + x +\angle XCY + y = 180^{\circ}</cmath> | <cmath>\theta + x +\angle XCY + y = 180^{\circ}</cmath> | ||
<cmath>180^{\circ} - \theta + y + \angle XDY + x = 180^{\circ}</cmath> | <cmath>180^{\circ} - \theta + y + \angle XDY + x = 180^{\circ}</cmath> | ||
| − | Cancelling out <math>180^{\circ}</math> in the second equation isolating <math>\theta</math> yields <math>\theta = y + \angle XDY + x</math>. Substituting <math>\theta</math> back into the first equation, we obtain | + | Cancelling out <math>180^{\circ}</math> in the second equation and isolating <math>\theta</math> yields <math>\theta = y + \angle XDY + x</math>. Substituting <math>\theta</math> back into the first equation, we obtain |
<cmath>2x + 2y + \angle XCY + \angle XDY = 180^{\circ}</cmath> | <cmath>2x + 2y + \angle XCY + \angle XDY = 180^{\circ}</cmath> | ||
Since | Since | ||
| Line 105: | Line 120: | ||
<cmath>37n \cdot 67n + 47^2 = 37 \cdot 67</cmath> | <cmath>37n \cdot 67n + 47^2 = 37 \cdot 67</cmath> | ||
<cmath>n^2 = \frac{270}{2479}</cmath> | <cmath>n^2 = \frac{270}{2479}</cmath> | ||
| − | Now, since <math>\angle AYX = x</math> and <math>\angle BYX = y</math>, <math>\angle AYB = x + y</math>. From there, let <math>\angle AYD = \alpha</math> and <math>\angle BYC = \beta</math>. From angle chasing we can derive that <math>\angle YDX = \angle YAX = \beta - x</math> and <math>\angle YCX = \angle YBX = \alpha - y</math>. From there, since <math>\angle ADX = x</math>, it is quite clear that <math>\angle ADY = \beta</math>, and <math>\angle YAB = \beta</math> can be found similarly. From there, since <math>\angle ADY = \angle YAB = \angle BYC = \beta</math> and <math>\angle DAY = \angle AYB = \angle YBC = x + y</math>, we have <math>AA</math> similarity between <math>\triangle DAY</math>, <math>\triangle AYB</math>, and <math>\triangle YBC</math>. Therefore the length of <math>AY</math> is the geometric mean of the lengths of <math>DA</math> and <math>YB</math> (from <math>\triangle DAY \sim \triangle AYB</math>). However, <math>\triangle DAY \sim \triangle AYB \sim \triangle YBC</math> yields the proportion <math>\frac{AD}{DY} = \frac{YA}{AB} = \frac{BY}{YC}</math>; | + | Now, since <math>\angle AYX = x</math> and <math>\angle BYX = y</math>, <math>\angle AYB = x + y</math>. From there, let <math>\angle AYD = \alpha</math> and <math>\angle BYC = \beta</math>. From angle chasing we can derive that <math>\angle YDX = \angle YAX = \beta - x</math> and <math>\angle YCX = \angle YBX = \alpha - y</math>. From there, since <math>\angle ADX = x</math>, it is quite clear that <math>\angle ADY = \beta</math>, and <math>\angle YAB = \beta</math> can be found similarly. From there, since <math>\angle ADY = \angle YAB = \angle BYC = \beta</math> and <math>\angle DAY = \angle AYB = \angle YBC = x + y</math>, we have <math>AA</math> similarity between <math>\triangle DAY</math>, <math>\triangle AYB</math>, and <math>\triangle YBC</math>. Therefore the length of <math>AY</math> is the geometric mean of the lengths of <math>DA</math> and <math>YB</math> (from <math>\triangle DAY \sim \triangle AYB</math>). However, <math>\triangle DAY \sim \triangle AYB \sim \triangle YBC</math> yields the proportion <math>\frac{AD}{DY} = \frac{YA}{AB} = \frac{BY}{YC}</math>; hence, the length of <math>AB</math> is the geometric mean of the lengths of <math>DY</math> and <math>YC</math>. |
We can now simply use arithmetic to calculate <math>AB^2</math>. | We can now simply use arithmetic to calculate <math>AB^2</math>. | ||
<cmath>AB^2 = DY \cdot YC</cmath> | <cmath>AB^2 = DY \cdot YC</cmath> | ||
| Line 112: | Line 127: | ||
'''-Solution by TheBoomBox77''' | '''-Solution by TheBoomBox77''' | ||
| + | ==Solution 5 (not too different)== | ||
| + | Let <math>E = DA \cap CB</math>. By Radical Axes, <math>E</math> lies on <math>XY</math>. Note that <math>EAXB</math> is cyclic as <math>X</math> is the Miquel point of <math>\triangle EDC</math> in this configuration. | ||
| + | |||
| + | Claim. <math>\triangle DXE \sim \triangle EXC</math> | ||
| + | Proof. We angle chase. <cmath>\measuredangle XEC = \measuredangle XEB = \measuredangle XAB = \measuredangle XDA = \measuredangle XDE</cmath>and<cmath>\measuredangle XCE = \measuredangle XCB = \measuredangle XBA = \measuredangle XEA = \measuredangle XED. \square</cmath> | ||
| + | |||
| + | Let <math>F = EX \cap AB</math>. Note <cmath>FA^2 = FX \cdot FY = FB^2</cmath>and<cmath>EF \cdot FX = AF \cdot FB = FA^2 = FX \cdot FY \implies EF = FY</cmath>By our claim, <cmath>\frac{DX}{XE} = \frac{EX}{XC} \implies EX^2 = DX \cdot XC = 67 \cdot 37 \implies FY = \frac{EY}{2} = \frac{EX+XY}{2} = \frac{\sqrt{67 \cdot 37}+47}{2}</cmath>and<cmath>FX=FY-47=\frac{\sqrt{67 \cdot 37}-47}{2}</cmath>Finally, <cmath>AB^2 = (2 \cdot FA)^2 = 4 \cdot FX \cdot FY = 4 \cdot \frac{(67 \cdot 37) - 47^2}{4} = \boxed{270}. \blacksquare</cmath>~Mathscienceclass | ||
| + | |||
| + | |||
| + | |||
| + | ==Solution 6 (No words)== | ||
| + | [[File:2016 AIME I 15.png|600px|right]] | ||
| + | [[File:2016 AIME I 15b.png|600px|left]] | ||
| + | |||
| + | <math>AB^2 = 4 AM^2 =2x(2x+ 2 XY) =(XP - XY) (XP + XY) = XP^2 - XY^2 = XC \cdot XD - XY^2 = 67 \cdot 37 - 47^2 = \boxed{270}.</math> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==Solution 7 (Linearity of Power of a Point)== | ||
| + | Extend <math>\overline{AD}</math> and <math>\overline{BC}</math> to meet at point <math>P</math>. Let <math>M</math> be the midpoint of segment <math>AB</math>. Then by radical axis on <math>(ADY)</math>, <math>(BCY)</math> and <math>(ABCD)</math>, <math>P</math> lies on <math>XY</math>. By the bisector lemma, <math>M</math> lies on <math>XY</math>. It is well-known that <math>P</math>, <math>A</math>, <math>X</math>, and <math>B</math> are concyclic. By Power of a point on <math>M</math> with respect to <math>(PAXB)</math> and <math>(ADY)</math>, <cmath> |\text{Pow}(M, (PAXB))| = MX \cdot MP = MA^2 = |\text{Pow}(M, (ADY))| = MX \cdot MY, </cmath> so <math>MP=MY</math>. Thus <math>AB</math> and <math>PY</math> bisect each other, so <math>PAYB</math> is a parallelogram. This implies that <cmath> \angle DAY = \angle YBC, </cmath> so by the inscribed angle theorem <math>\overline{XY}</math> bisects <math>\angle DXC</math>. | ||
| + | |||
| + | Claim: <math>AB^2 = DY \cdot YC</math>. | ||
| + | |||
| + | Proof. Define the linear function <math>f(\bullet) := \text{Pow}(\bullet, (ADY)) - \text{Pow}(\bullet, (ABCD))</math>. Since <math>\overline{BY}</math> is parallel to the radical axis <math>\overline{AD}</math> of <math>(ADY)</math> and <math>(ABCD)</math> by our previous parallelism, <math>f(B)=f(Y)</math>. Note that <math>f(B)=AB^2</math> while <math>f(Y)=DY \cdot YC</math>, so we conclude. <math>\square</math> | ||
| + | |||
| + | By Stewart's theorem on <math>\triangle DXC</math>, <math>DY \cdot YC=37 \cdot 67 - 47^2 = 270</math>, so <math>AB^2=\boxed{270}</math>. | ||
| + | |||
| + | ~ Leo.Euler | ||
| + | |||
| + | ==Video Solution by MOP 2024== | ||
| + | https://youtu.be/qFfgB15fYS8 | ||
| + | |||
| + | ~r00tsOfUnity | ||
| + | |||
| + | ==Video Solution== | ||
| + | https://youtu.be/QoVIorvv_I8 | ||
| + | |||
| + | ~MathProblemSolvingSkills.com | ||
| + | |||
| + | ==Video Solution by The Power of Logic== | ||
| + | https://youtu.be/lTZx6tp2Fvg | ||
==See Also== | ==See Also== | ||
{{AIME box|year=2016|n=I|num-b=14|after=Last Question}} | {{AIME box|year=2016|n=I|num-b=14|after=Last Question}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Latest revision as of 16:12, 8 January 2024
Contents
Problem
Circles ![]() and
and ![]() intersect at points
intersect at points ![]() and
and ![]() . Line
. Line ![]() is tangent to
is tangent to ![]() and
and ![]() at
at ![]() and
and ![]() , respectively, with line
, respectively, with line ![]() closer to point
closer to point ![]() than to
than to ![]() . Circle
. Circle ![]() passes through
passes through ![]() and
and ![]() intersecting
intersecting ![]() again at
again at ![]() and intersecting
and intersecting ![]() again at
again at ![]() . The three points
. The three points ![]() ,
, ![]() ,
, ![]() are collinear,
are collinear, ![]() ,
, ![]() , and
, and ![]() . Find
. Find ![]() .
.
Solution
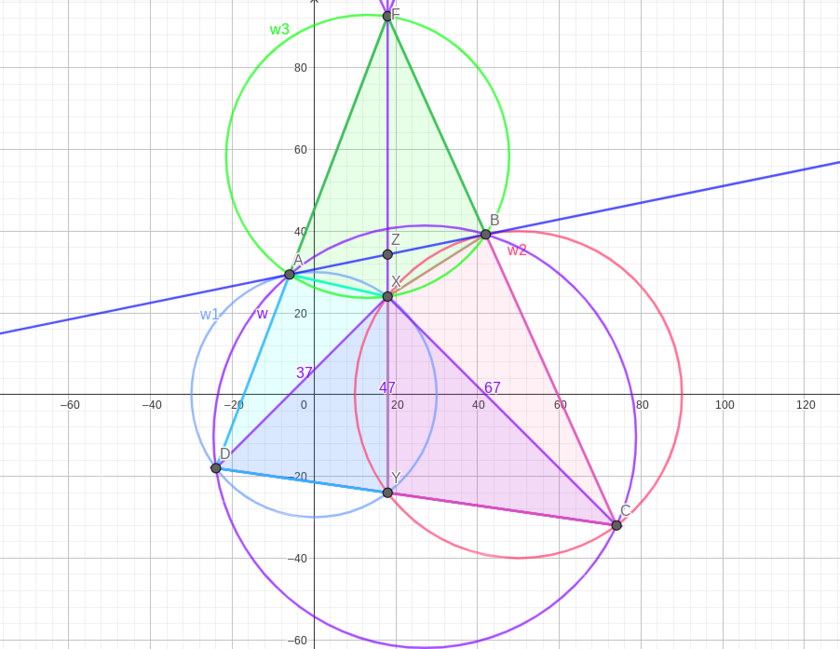
Using the radical axis theorem, the lines ![]() are all concurrent at one point, call it
are all concurrent at one point, call it ![]() . Now recall by Miquel's theorem in
. Now recall by Miquel's theorem in ![]() the fact that quadrilaterals
the fact that quadrilaterals ![]() and
and ![]() are cyclic implies
are cyclic implies ![]() is cyclic as well. Denote
is cyclic as well. Denote ![]() and
and ![]() .
.
Since point ![]() lies on the radical axis of
lies on the radical axis of ![]() , it has equal power with respect to both circles, thus
, it has equal power with respect to both circles, thus ![]() Also, notice that
Also, notice that ![]() The diagonals of quadrilateral
The diagonals of quadrilateral ![]() bisect each other at
bisect each other at ![]() , so we conclude that
, so we conclude that ![]() is a parallelogram. Let
is a parallelogram. Let ![]() , so that
, so that ![]() .
.
Because ![]() is a parallelogram and quadrilaterals
is a parallelogram and quadrilaterals ![]() are cyclic,
are cyclic, ![]() so we have the pair of similar triangles
so we have the pair of similar triangles ![]() . Thus
. Thus ![]() Now compute
Now compute ![]()
Solution 1
Let ![]() . By the radical axis theorem
. By the radical axis theorem ![]() are concurrent, say at
are concurrent, say at ![]() . Moreover,
. Moreover, ![]() by simple angle chasing. Let
by simple angle chasing. Let ![]() . Then
. Then ![]() Now,
Now, ![]() , and by power of a point,
, and by power of a point,  Solving, we get
Solving, we get ![]()
![]()
Solution 2
By the Radical Axis Theorem ![]() concur at point
concur at point ![]() .
.
Let ![]() and
and ![]() intersect at
intersect at ![]() . Note that because
. Note that because ![]() and
and ![]() are cyclic, by Miquel's Theorem
are cyclic, by Miquel's Theorem ![]() is cyclic as well. Thus
is cyclic as well. Thus
![]() and
and
![]() Thus
Thus ![]() and
and ![]() , so
, so ![]() is a parallelogram. Hence
is a parallelogram. Hence ![]() and
and ![]() . But notice that
. But notice that ![]() and
and ![]() are similar by
are similar by ![]() Similarity, so
Similarity, so ![]() . But
. But
![]() Hence
Hence ![]()
Solution 3
First, we note that as ![]() and
and ![]() have bases along the same line,
have bases along the same line, ![]() . We can also find the ratio of their areas using the circumradius area formula. If
. We can also find the ratio of their areas using the circumradius area formula. If ![]() is the radius of
is the radius of ![]() and if
and if ![]() is the radius of
is the radius of ![]() , then
, then
![]() Since we showed this to be
Since we showed this to be ![]() , we see that
, we see that ![]() .
.
We extend ![]() and
and ![]() to meet at point
to meet at point ![]() , and we extend
, and we extend ![]() and
and ![]() to meet at point
to meet at point ![]() as shown below.
as shown below.
![[asy] size(200); import olympiad; real R1=45,R2=67*R1/37; real m1=sqrt(R1^2-23.5^2); real m2=sqrt(R2^2-23.5^2); pair o1=(0,0),o2=(m1+m2,0),x=(m1,23.5),y=(m1,-23.5); draw(circle(o1,R1)); draw(circle(o2,R2)); pair q=(-R1/(R2-R1)*o2.x,0); pair a=tangent(q,o1,R1,2); pair b=tangent(q,o2,R2,2); pair d=intersectionpoints(circle(o1,R1),q--y+15*(y-q))[0]; pair c=intersectionpoints(circle(o2,R2),q--y+15*(y-q))[1]; pair p=extension(a,d,b,c); dot(q^^a^^b^^x^^y^^c^^d^^p); draw(q--b^^q--c); draw(p--d^^p--c^^x--y); draw(a--y^^b--y); draw(d--x--c); label("$A$",a,NW,fontsize(8)); label("$B$",b,NE,fontsize(8)); label("$C$",c,SE,fontsize(8)); label("$D$",d,SW,fontsize(8)); label("$X$",x,2*WNW,fontsize(8)); label("$Y$",y,3*S,fontsize(8)); label("$P$",p,N,fontsize(8)); label("$Q$",q,W,fontsize(8)); [/asy]](http://latex.artofproblemsolving.com/2/0/0/200feab33999ae63954444617d1c3d67d4a2b23b.png) As
As ![]() is cyclic, we know that
is cyclic, we know that ![]() . But then as
. But then as ![]() is tangent to
is tangent to ![]() at
at ![]() , we see that
, we see that ![]() . Therefore,
. Therefore, ![]() , and
, and ![]() . A similar argument shows
. A similar argument shows ![]() . These parallel lines show
. These parallel lines show ![]() . Also, we showed that
. Also, we showed that ![]() , so the ratio of similarity between
, so the ratio of similarity between ![]() and
and ![]() is
is ![]() , or rather
, or rather
![]() We can now use the parallel lines to find more similar triangles. As
We can now use the parallel lines to find more similar triangles. As ![]() , we know that
, we know that
![]() Setting
Setting ![]() , we see that
, we see that ![]() , hence
, hence ![]() , and the problem simplifies to finding
, and the problem simplifies to finding ![]() . Setting
. Setting ![]() , we also see that
, we also see that ![]() , hence
, hence ![]() . Also, as
. Also, as ![]() , we find that
, we find that
![]() As
As ![]() , we see that
, we see that ![]() , hence
, hence ![]() .
.
Applying Power of a Point to point ![]() with respect to
with respect to ![]() , we find
, we find
![]() or
or ![]() . We wish to find
. We wish to find ![]() .
.
Applying Stewart's Theorem to ![]() , we find
, we find
![]() We can cancel
We can cancel ![]() from both sides, finding
from both sides, finding ![]() . Therefore,
. Therefore,
![]()
Solution 4
![[asy] size(9cm); import olympiad; real R1=45,R2=67*R1/37; real m1=sqrt(R1^2-23.5^2); real m2=sqrt(R2^2-23.5^2); pair o1=(0,0),o2=(m1+m2,0),x=(m1,23.5),y=(m1,-23.5); draw(circle(o1,R1)); draw(circle(o2,R2)); pair q=(-R1/(R2-R1)*o2.x,0); pair a=tangent(q,o1,R1,2); pair b=tangent(q,o2,R2,2); pair d=intersectionpoints(circle(o1,R1),q--y+15*(y-q))[0]; pair c=intersectionpoints(circle(o2,R2),q--y+15*(y-q))[1]; dot(a^^b^^x^^y^^c^^d); draw(x--y); draw(a--y^^b--y); draw(d--x--c); draw(a--b--c--d--cycle); draw(x--a^^x--b); label("$A$",a,NW,fontsize(9)); label("$B$",b,NE,fontsize(9)); label("$C$",c,SE,fontsize(9)); label("$D$",d,SW,fontsize(9)); label("$X$",x,2*N,fontsize(9)); label("$Y$",y,3*S,fontsize(9)); [/asy]](http://latex.artofproblemsolving.com/9/e/d/9edab2433cc7ad4e4413fc95f45b47d01eae4a00.png) First of all, since quadrilaterals
First of all, since quadrilaterals ![]() and
and ![]() are cyclic, we can let
are cyclic, we can let ![]() , and
, and ![]() , due to the properties of cyclic quadrilaterals. In addition, let
, due to the properties of cyclic quadrilaterals. In addition, let ![]() and
and ![]() . Thus,
. Thus, ![]() and
and ![]() . Then, since quadrilateral
. Then, since quadrilateral ![]() is cyclic as well, we have the following sums:
is cyclic as well, we have the following sums:
![]()
![]() Cancelling out
Cancelling out ![]() in the second equation and isolating
in the second equation and isolating ![]() yields
yields ![]() . Substituting
. Substituting ![]() back into the first equation, we obtain
back into the first equation, we obtain
![]() Since
Since
![]()
![]() we can then imply that
we can then imply that ![]() . Similarly,
. Similarly, ![]() . So then
. So then ![]() , so since we know that
, so since we know that ![]() bisects
bisects ![]() , we can solve for
, we can solve for ![]() and
and ![]() with Stewart’s Theorem. Let
with Stewart’s Theorem. Let ![]() and
and ![]() . Then
. Then
![]()
![]()
![]() Now, since
Now, since ![]() and
and ![]() ,
, ![]() . From there, let
. From there, let ![]() and
and ![]() . From angle chasing we can derive that
. From angle chasing we can derive that ![]() and
and ![]() . From there, since
. From there, since ![]() , it is quite clear that
, it is quite clear that ![]() , and
, and ![]() can be found similarly. From there, since
can be found similarly. From there, since ![]() and
and ![]() , we have
, we have ![]() similarity between
similarity between ![]() ,
, ![]() , and
, and ![]() . Therefore the length of
. Therefore the length of ![]() is the geometric mean of the lengths of
is the geometric mean of the lengths of ![]() and
and ![]() (from
(from ![]() ). However,
). However, ![]() yields the proportion
yields the proportion ![]() ; hence, the length of
; hence, the length of ![]() is the geometric mean of the lengths of
is the geometric mean of the lengths of ![]() and
and ![]() .
We can now simply use arithmetic to calculate
.
We can now simply use arithmetic to calculate ![]() .
.
![]()
![]()
![]()
-Solution by TheBoomBox77
Solution 5 (not too different)
Let ![]() . By Radical Axes,
. By Radical Axes, ![]() lies on
lies on ![]() . Note that
. Note that ![]() is cyclic as
is cyclic as ![]() is the Miquel point of
is the Miquel point of ![]() in this configuration.
in this configuration.
Claim. ![]() Proof. We angle chase.
Proof. We angle chase. ![]() and
and![]()
Let ![]() . Note
. Note ![]() and
and![]() By our claim,
By our claim, ![]() and
and![]() Finally,
Finally, ![]() ~Mathscienceclass
~Mathscienceclass
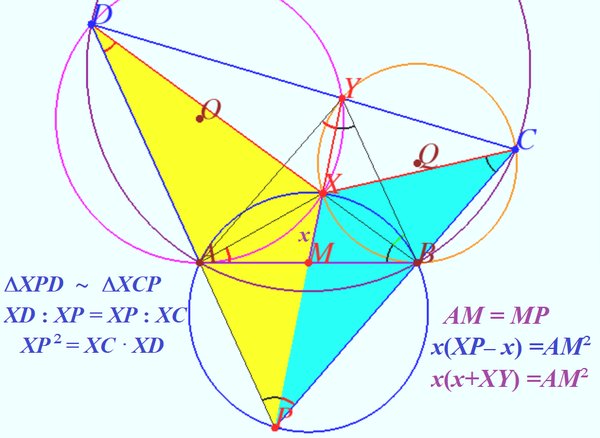
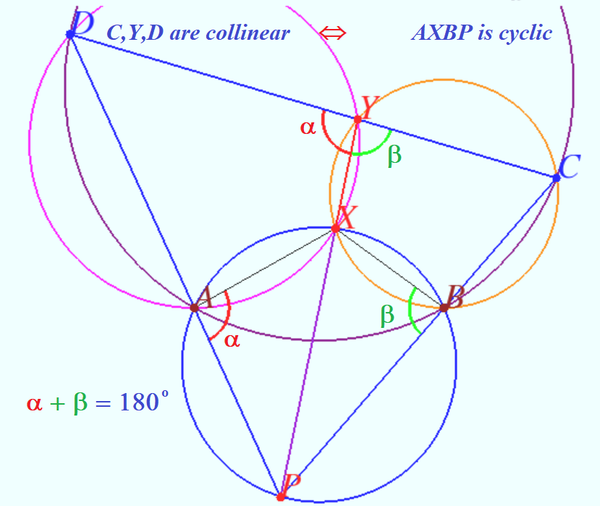
Solution 6 (No words)
![]()
vladimir.shelomovskii@gmail.com, vvsss
Solution 7 (Linearity of Power of a Point)
Extend ![]() and
and ![]() to meet at point
to meet at point ![]() . Let
. Let ![]() be the midpoint of segment
be the midpoint of segment ![]() . Then by radical axis on
. Then by radical axis on ![]() ,
, ![]() and
and ![]() ,
, ![]() lies on
lies on ![]() . By the bisector lemma,
. By the bisector lemma, ![]() lies on
lies on ![]() . It is well-known that
. It is well-known that ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are concyclic. By Power of a point on
are concyclic. By Power of a point on ![]() with respect to
with respect to ![]() and
and ![]() ,
, ![]() so
so ![]() . Thus
. Thus ![]() and
and ![]() bisect each other, so
bisect each other, so ![]() is a parallelogram. This implies that
is a parallelogram. This implies that ![]() so by the inscribed angle theorem
so by the inscribed angle theorem ![]() bisects
bisects ![]() .
.
Claim: ![]() .
.
Proof. Define the linear function ![]() . Since
. Since ![]() is parallel to the radical axis
is parallel to the radical axis ![]() of
of ![]() and
and ![]() by our previous parallelism,
by our previous parallelism, ![]() . Note that
. Note that ![]() while
while ![]() , so we conclude.
, so we conclude. ![]()
By Stewart's theorem on ![]() ,
, ![]() , so
, so ![]() .
.
~ Leo.Euler
Video Solution by MOP 2024
~r00tsOfUnity
Video Solution
~MathProblemSolvingSkills.com
Video Solution by The Power of Logic
See Also
| 2016 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Last Question | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.