Difference between revisions of "2017 AMC 12B Problems/Problem 24"

Latest revision as of 17:06, 31 July 2024

Problem

Quadrilateral $ABCD$ has right angles at $B$ and $C$ , $\triangle ABC \sim \triangle BCD$ , and $AB > BC$ . There is a point $E$ in the interior of $ABCD$ such that $\triangle ABC \sim \triangle CEB$ and the area of $\triangle AED$ is $17$ times the area of $\triangle CEB$ . What is $\tfrac{AB}{BC}$ ?

$\textbf{(A) } 1+\sqrt{2} \qquad \textbf{(B) } 2 + \sqrt{2} \qquad \textbf{(C) } \sqrt{17} \qquad \textbf{(D) } 2 + \sqrt{5} \qquad \textbf{(E) } 1 + 2\sqrt{3}$

Solution 1

Let $CD=1$ , $BC=x$ , and $AB=x^2$ . Note that $AB/BC=x$ . By the Pythagorean Theorem, $BD=\sqrt{x^2+1}$ . Since $\triangle BCD \sim \triangle ABC \sim \triangle CEB$ , the ratios of side lengths must be equal. Since $BC=x$ , $CE=\frac{x^2}{\sqrt{x^2+1}}$ and $BE=\frac{x}{\sqrt{x^2+1}}$ . Let F be a point on $\overline{BC}$ such that $\overline{EF}$ is an altitude of triangle $CEB$ . Note that $\triangle CEB \sim \triangle CFE \sim \triangle EFB$ . Therefore, $BF=\frac{x}{x^2+1}$ and $CF=\frac{x^3}{x^2+1}$ . Since $\overline{CF}$ and $\overline{BF}$ form altitudes of triangles $CED$ and $BEA$ , respectively, the areas of these triangles can be calculated. Additionally, the area of triangle $BEC$ can be calculated, as it is a right triangle. Solving for each of these yields:

\begin{align*} [BEC] &=[CED]=[BEA]=\frac{x^3}{2(x^2+1)} \\ [ABCD] &=[AED]+[DEC]+[CEB]+[BEA] \\ \frac{(BC)(AB+CD)}{2} &= 17*[CEB]+ [CEB] + [CEB] + [CEB] \\ \frac{x^3+x}{2} &= \frac{20x^3}{2(x^2+1)} \\ \frac{x}{x^2+1} &= \frac{20x^3}{x^2+1} \\ (x^2+1)^2 &=20x^2 \\ x^4-18x^2+1 &=0 \implies x^2=9+4\sqrt{5}=4+2(2\sqrt{5})+5 \\ \end{align*}

Therefore, the answer is $\boxed{\textbf{(D) } 2+\sqrt{5}}$

Solution 2

Draw line $FG$ through $E$ , with $F$ on $BC$ and $G$ on $AD$ , $FG \parallel AB$ . WLOG let $CD=1$ , $CB=x$ , $AB=x^2$ . By weighted average $FG=\frac{1+x^4}{1+x^2}$ .

Meanwhile, $FE:EG=[\triangle CBE]:[\triangle ADE]=1:17$ . This follows from comparing the ratios of triangle DEG to CFE and triangle AEG to FEB, both pairs in which the two triangles share a height perpendicular to FG, and have base ratio $EG:FE$ .

$FE=\frac{x^2}{1+x^2}$ . We obtain $\frac{1+x^4}{1+x^2}=\frac{18x^2}{1+x^2}$ , namely $x^4-18x^2+1=0$ .

The rest is the same as Solution 1.

Solution 3

Let $AB = a$ , $BC = b$ , $AC = \sqrt{a^2+b^2}$

Note that $E$ cannot be the intersection of $AC$ and $BD$ , as that would mean $[AED] = [CEB]$

$\because \triangle BCD \sim \triangle ABC, \quad \therefore \frac{CD}{BC} = \frac{BC}{AB}, \quad CD = BC \cdot \frac{BC}{AB} = b \cdot \frac{b}{a} = \frac{b^2}{a}$

$[CEB] = ( \frac{BC}{AC} )^2 \cdot [ABC] = ( \frac{b}{ \sqrt{a^2+b^2} } )^2 \cdot \frac{ab}{2} = \frac{ab^3}{2(a^2+b^2)}$

$BF = \frac{ 2[CEB] }{BC} = \frac{ 2 \cdot \frac{ab^3}{ 2(a^2+b^2) } }{b} = \frac{ab^2}{a^2+b^2}$

$\because \triangle BFE \sim \triangle ABC, \quad \therefore \frac{EF}{BF} = \frac{BC}{AB}, \quad EF = BF \cdot \frac{BC}{AB} = \frac{ab^2}{a^2+b^2} \cdot \frac{b}{a} = \frac{b^3}{a^2+b^2}$

$EG = FG - EF = b - \frac{b^3}{a^2+b^2} = \frac{a^2b}{a^2+b^2}$

$[ABCD] = \frac{AB + CD}{2} \cdot BC = \frac{a + \frac{b^2}{a} }{2} \cdot b = \frac{ b(a^2+b^2) }{ 2a }$

$[ABE] = \frac12 \cdot AB \cdot EF = \frac12 \cdot a \cdot \frac{b^3}{a^2+b^2} = \frac{ab^3}{ 2(a^2+b^2) }$

$[CDE] = \frac12 \cdot CD \cdot EG = \frac12 \cdot \frac{a^2b}{a^2+b^2} \cdot \frac{a^2b}{a^2+b^2} = \frac{ab^3}{ 2(a^2+b^2) }$

$ADE = [ABCD] - [ABE] - [CEB] - [CDE] = \frac{ b(a^2+b^2) }{ 2a } - \frac{ab^3}{ 2(a^2+b^2) } - \frac{ab^3}{ 2(a^2+b^2) }- \frac{ab^3}{ 2(a^2+b^2) } = \frac{ b(a^2+b^2)^2 - 3a^2b^3 }{ 2a(a^2+b^2) }$

$\frac{ [ADE] }{ [CEB] } = \frac { \frac{ b(a^2+b^2)^2 - 3a^2b^3 }{ 2a(a^2+b^2) } }{ \frac{ab^3}{2(a^2+b^2)} } = \frac{ (a^2 + b^2)^2 - 3a^2b^2 }{ a^2b^2 } = \frac{ a^4 - a^2b^2 + b^4 }{ a^2b^2 } = 17$

$a^4 - a^2b^2 + b^4 = 17 a^2b^2, \quad a^4 + b^4 = 18 a^2b^2, \quad \frac{a^2}{b^2} + \frac{b^2}{a^2} = 18$

Let $x = \frac{a}{b}$ ,

$x^2 + \frac{1}{x^2} = 18, \quad x^4 - 18x^2 + 1 = 0, \quad x^2 = \frac{18 + \sqrt{324-4} }{2} = 9+ 4\sqrt{5}$

$\frac{a}{b} = \sqrt{ 9+ 4\sqrt{5} } = \sqrt{ 4+ 4\sqrt{5}+5 } = \boxed{\textbf{(D) } 2+ \sqrt{5}}$

~isabelchen

Solution 4

Let $A=(-1,4a), B=(-1,0), C=(1,0), D=\bigg(1,\frac{1}{a}\bigg)$ . Then from the similar triangles condition, we compute $CE=\frac{4a}{\sqrt{4a^2+1}}$ and $BE=\frac{2}{\sqrt{4a^2+1}}$ . Hence, the $y$ -coordinate of $E$ is just $\frac{BE\cdot CE}{BC}=\frac{4a}{4a^2+1}$ . Since $E$ lies on the unit circle, we can compute the $x$ coordinate as $\frac{1-4a^2}{4a^2+1}$ . By Shoelace, we want $\frac{1}{2}\det\begin{bmatrix} -1 & 4a & 1\\ \frac{1-4a^2}{4a^2+1} & \frac{4a}{4a^2+1} & 1\\ 1 & \frac{1}{a} & 1 \end{bmatrix}=17\cdot\frac{1}{2}\cdot 2 \cdot \frac{4a}{4a^2+1}$ Factoring out denominators and expanding by minors, this is equivalent to $\frac{32a^4-8a^2+2}{2a(4a^2+1)}=\frac{68a}{4a^2+1} \Longrightarrow 16a^4-72a^2+1=0$ This factors as $(4a^2-8a-1)(4a^2+8a-1)=0$ , so $a=1+\frac{\sqrt{5}}{2}$ and so the answer is $\textbf{(D) \ }$ .

Solution 5

Let $C = (0,0), D=(\frac1a, 0), B = (0,1), A = (a,1)$ where $a>1$ . Because $BC = 1, a = \frac{AB}{BC}$ . Notice that the diagonals are perpendicular with slopes of $\frac1a$ and $-a$ . Let the intersection of $AC$ and $BD$ be $F$ , then $\triangle BFC \sim \triangle ABC$ . However, because $ABCD$ is a trapezoid, $\triangle$ $BCF$ and $\triangle ADF$ share the same area, therefore $\triangle$ $BCE$ is the reflection of $\triangle$ $BCF$ over the perpendicular bisector of $BC$ , which is $y=\frac12$ . We use the linear equations of the diagonals, $y = -ax + 1, y = \frac1a x$ , to find the coordinates of $F$ . $-ax+1 = \frac1ax \Longrightarrow x = \frac{1}{a+\frac1a} = \frac{a}{a^2+1}$ $y = \frac1ax = \frac{1}{a^2+1}$ The y-coordinate of $E$ is simply $1-\frac{1}{a^2+1} = \frac{a^2}{a^2+1}$ The area of $\triangle BCE$ is $\frac12 \frac{a}{a^2+1}$ . We apply shoelace theorem to solve for the area of $\triangle ADE$ . The coordinates of the triangle are $\{(\frac{a}{a^2+1}, \frac{a^2}{a^2+1}), (a,1), (\frac1a, 0)\}$ , so the area is

$\frac12 |\frac{a^3}{a^2+1} + \frac1a - \frac{a}{a^2+1} - \frac{a}{a^2+1}| = \frac12 |\frac{a^3-2a}{a^2+1} + \frac1a|$ $= \frac12 |\frac{a^4-2a^2}{a(a^2+1)} + \frac{a^2+1}{a(a^2+1)}| = \frac12 \frac{a^4-a^2+1}{a(a^2+1)}$ Finally, we use the property that the ratio of areas equals $17$ $\frac{\frac12}{\frac12} \frac{\frac{a^4-a^2+1}{a(a^2+1)}}{\frac{a}{a^2+1}} = 17 \Rightarrow \frac{a^4-a^2+1}{a^2} = 17 \Rightarrow a^4-18a^2+1 = 0$ $a^2 = 9+4\sqrt{5} = (2+\sqrt{5})^2 \Longrightarrow a = \boxed{\textbf{(D) } 2+\sqrt{5}}$

~Zeric

Solution 6

This solution involves proving $\triangle AED \sim \triangle CEB$ .

Let $E'$ be the intersection of $AC$ and $BD$ . Label points $F$ and $G$ the same way as $\textbf{Solution 3}$ .

$\angle AE'D = \angle CE'B = \frac{\pi}{2} = \angle AFE$ . Additionally, $\frac{E'D}{FE} = \frac{E'D}{E'G} = \frac{AE'}{AF}$ , so $\triangle AFE \sim \triangle AE'D$ by SAS. Therefore, $\angle BAC = \angle FAE + \angle EAE' = \angle E'AD + \angle EAE' = \angle EAD$ .

Next, $\angle AFE = \frac{\pi}{2} = \angle EGD$ because $FG \parallel BC$ . Also, $\pi = \angle FEA + \angle AED + \angle DEG = \angle FEA + \angle AED + \angle EAF = \frac{\pi}{2} + \angle AED$ , so $\angle AED = \frac{\pi}{2}$ . Therefore, $\triangle AED \sim \triangle ABC$ by AA. Since $\triangle CEB \sim \triangle ABC$ , $\triangle AED \sim \triangle CEB$ .

Given $\frac{[AED]}{[CEB]} = 17$ , we deduce that the ratio of corresponding side lengths of $AED$ to $CEB$ must be $\sqrt{17}$ . Now, we set $BC = 1$ , $AB = x$ , and $CD = \frac{1}{x}$ . Using the Pythagorean Theorem, $AD = \sqrt{\Big(x-\frac{1}{x}\Big)^2 + 1^2}$ . Thus, $\sqrt{17} = \frac{AD}{CB} = \frac{\sqrt{\Big(x-\frac{1}{x}\Big)^2 + 1^2}}{1}$ . Solving gives $x = 2+\sqrt{5}$ .

Finally, $\frac{AB}{BC} = \frac{2+\sqrt{5}}{1} = \boxed{\textbf{(D) } 2+\sqrt{5}}$ .

~Zhixing

Video Solution by MOP 2024

https://youtu.be/h92s2BxlohI

~r00tsOfUnity

Notes

1) $\sqrt{17}$ is the most relevant answer choice because it shares numbers with the givens of the problem.

2) It's a very good guess to replace finding the area of triangle AED with the area of the triangle DAF, where F is the projection of D onto AB(then find the closest answer choice).

@@ Line 1: / Line 1: @@
 ==Problem==
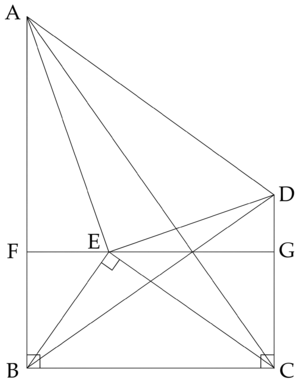
-Quadrilateral <math>ABCD</math> has right angles at <math>B</math> and <math>C</math>, <math>\triangle ABC</math> is similar to <math>\triangle BCD</math>, and <math>AB > BC</math>. There exists a point <math>E</math> in the interior of <math>ABCD</math> such that <math>\triangle ABC</math> is similar to <math>\triangle CEB</math> and the area of Triangle <math>AED</math> is <math>17</math> times the area of Triangle <math>CEB</math>. Find <math>AB/BC</math>.
+Quadrilateral <math>ABCD</math> has right angles at <math>B</math> and <math>C</math>, <math>\triangle ABC \sim \triangle BCD</math>, and <math>AB > BC</math>. There is a point <math>E</math> in the interior of <math>ABCD</math> such that <math>\triangle ABC \sim \triangle CEB</math> and the area of <math>\triangle AED</math> is <math>17</math> times the area of <math>\triangle CEB</math>. What is <math>\tfrac{AB}{BC}</math>?
 <math>\textbf{(A) } 1+\sqrt{2} \qquad \textbf{(B) } 2 + \sqrt{2} \qquad \textbf{(C) } \sqrt{17} \qquad \textbf{(D) } 2 + \sqrt{5} \qquad \textbf{(E) } 1 + 2\sqrt{3}</math>
-==Solution==
+==Solution 1==
 Let <math>CD=1</math>, <math>BC=x</math>, and <math>AB=x^2</math>. Note that <math>AB/BC=x</math>. By the Pythagorean Theorem, <math>BD=\sqrt{x^2+1}</math>. Since <math>\triangle BCD \sim \triangle ABC \sim \triangle CEB</math>, the ratios of side lengths must be equal. Since <math>BC=x</math>, <math>CE=\frac{x^2}{\sqrt{x^2+1}}</math> and <math>BE=\frac{x}{\sqrt{x^2+1}}</math>. Let F be a point on <math>\overline{BC}</math> such that <math>\overline{EF}</math> is an altitude of triangle <math>CEB</math>. Note that <math>\triangle CEB \sim \triangle CFE \sim \triangle EFB</math>. Therefore, <math>BF=\frac{x}{x^2+1}</math> and <math>CF=\frac{x^3}{x^2+1}</math>. Since <math>\overline{CF}</math> and <math>\overline{BF}</math> form altitudes of triangles <math>CED</math> and <math>BEA</math>, respectively, the areas of these triangles can be calculated. Additionally, the area of triangle <math>BEC</math> can be calculated, as it is a right triangle. Solving for each of these yields:
-<cmath>[BEC]=[CED]=[BEA]=(x^3)/(2(x^2+1))</cmath>
-<cmath>[ABCD]=[AED]+[DEC]+[CEB]+[BEA]</cmath>
+\begin{align*}
-<cmath>(AB+CD)(BC)/2= 17*[CEB]+ [CEB] + [CEB] + [CEB]</cmath>
+[BEC] &=[CED]=[BEA]=\frac{x^3}{2(x^2+1)} \\
-<cmath>(x^3+x)/2=(20x^3)/(2(x^2+1))</cmath>
+[ABCD] &=[AED]+[DEC]+[CEB]+[BEA] \\
-<cmath>(x)(x^2+1)=20x^3/(x^2+1)</cmath>
+\frac{(BC)(AB+CD)}{2} &= 17*[CEB]+ [CEB] + [CEB] + [CEB] \\
-<cmath>(x^2+1)^2=20x^2</cmath>
+\frac{x^3+x}{2} &= \frac{20x^3}{2(x^2+1)} \\
-<cmath>x^4-18x^2+1=0 \implies x^2=9+4\sqrt{5}=4+2(2\sqrt{5})+5</cmath>
+\frac{x}{x^2+1} &= \frac{20x^3}{x^2+1} \\
+(x^2+1)^2 &=20x^2 \\
+x^4-18x^2+1 &=0 \implies x^2=9+4\sqrt{5}=4+2(2\sqrt{5})+5 \\
+\end{align*}
 Therefore, the answer is <math>\boxed{\textbf{(D) } 2+\sqrt{5}}</math>
+==Solution 2==
+Draw line <math>FG</math> through <math>E</math>, with <math>F</math> on <math>BC</math> and <math>G</math> on <math>AD</math>, <math>FG \parallel AB</math>. WLOG let <math>CD=1</math>, <math>CB=x</math>, <math>AB=x^2</math>. By weighted average <math>FG=\frac{1+x^4}{1+x^2}</math>.
+Meanwhile, <math>FE:EG=[\triangle CBE]:[\triangle ADE]=1:17</math>. This follows from comparing the ratios of triangle DEG to CFE and triangle AEG to FEB, both pairs in which the two triangles share a height perpendicular to FG, and have base ratio <math>EG:FE</math>.
+<math>FE=\frac{x^2}{1+x^2}</math>. We obtain <math>\frac{1+x^4}{1+x^2}=\frac{18x^2}{1+x^2}</math>,
+namely <math>x^4-18x^2+1=0</math>.
+The rest is the same as Solution 1.
+==Solution 3==
+[[File:2017AMC12BP24.png|300px|center]]
+Let <math>AB = a</math>, <math>BC = b</math>, <math>AC = \sqrt{a^2+b^2}</math>
+Note that <math>E</math> cannot be the intersection of <math>AC</math> and <math>BD</math>, as that would mean <math>[AED] = [CEB]</math>
+<cmath>\because \triangle BCD \sim \triangle ABC, \quad \therefore \frac{CD}{BC} = \frac{BC}{AB}, \quad CD = BC \cdot \frac{BC}{AB} = b \cdot \frac{b}{a} = \frac{b^2}{a}</cmath>
+<cmath>[CEB] = ( \frac{BC}{AC} )^2 \cdot [ABC] = ( \frac{b}{ \sqrt{a^2+b^2} } )^2 \cdot \frac{ab}{2} = \frac{ab^3}{2(a^2+b^2)}</cmath>
+<cmath>BF = \frac{ 2[CEB] }{BC} = \frac{ 2 \cdot \frac{ab^3}{ 2(a^2+b^2) } }{b} = \frac{ab^2}{a^2+b^2}</cmath>
+<cmath>\because \triangle BFE \sim \triangle ABC, \quad \therefore \frac{EF}{BF} = \frac{BC}{AB}, \quad EF = BF \cdot \frac{BC}{AB} = \frac{ab^2}{a^2+b^2} \cdot \frac{b}{a} = \frac{b^3}{a^2+b^2}</cmath>
+<cmath>EG = FG - EF = b - \frac{b^3}{a^2+b^2} = \frac{a^2b}{a^2+b^2}</cmath>
+<cmath>[ABCD] = \frac{AB + CD}{2} \cdot BC = \frac{a + \frac{b^2}{a} }{2} \cdot b = \frac{ b(a^2+b^2) }{ 2a }</cmath>
+<cmath>[ABE] = \frac12 \cdot AB \cdot EF = \frac12 \cdot a \cdot \frac{b^3}{a^2+b^2} = \frac{ab^3}{ 2(a^2+b^2) }</cmath>
+<cmath>[CDE] = \frac12 \cdot CD \cdot EG = \frac12 \cdot \frac{a^2b}{a^2+b^2} \cdot \frac{a^2b}{a^2+b^2} = \frac{ab^3}{ 2(a^2+b^2) }</cmath>
+<cmath>ADE = [ABCD] - [ABE] - [CEB] - [CDE] = \frac{ b(a^2+b^2) }{ 2a } - \frac{ab^3}{ 2(a^2+b^2) } - \frac{ab^3}{ 2(a^2+b^2) }- \frac{ab^3}{ 2(a^2+b^2) } = \frac{ b(a^2+b^2)^2 - 3a^2b^3 }{ 2a(a^2+b^2) } </cmath>
+<cmath>\frac{ [ADE] }{ [CEB] } = \frac { \frac{ b(a^2+b^2)^2 - 3a^2b^3 }{ 2a(a^2+b^2) } }{ \frac{ab^3}{2(a^2+b^2)} } = \frac{
+(a^2 + b^2)^2 - 3a^2b^2 }{ a^2b^2 } = \frac{ a^4 - a^2b^2 + b^4 }{ a^2b^2 } = 17</cmath>
+<cmath>a^4 - a^2b^2 + b^4 = 17 a^2b^2, \quad a^4 + b^4 = 18 a^2b^2, \quad \frac{a^2}{b^2} + \frac{b^2}{a^2} = 18</cmath>
+Let <math>x = \frac{a}{b}</math>,
+<cmath>x^2 + \frac{1}{x^2} = 18, \quad x^4 - 18x^2 + 1 = 0, \quad x^2 = \frac{18 + \sqrt{324-4} }{2} = 9+ 4\sqrt{5}</cmath>
+<cmath>\frac{a}{b} = \sqrt{ 9+ 4\sqrt{5} } = \sqrt{ 4+ 4\sqrt{5}+5 } = \boxed{\textbf{(D) } 2+ \sqrt{5}}</cmath>
+~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen]
+== Solution 4==
+Let <math>A=(-1,4a), B=(-1,0), C=(1,0), D=\bigg(1,\frac{1}{a}\bigg)</math>. Then from the similar triangles condition, we compute <math>CE=\frac{4a}{\sqrt{4a^2+1}}</math> and <math>BE=\frac{2}{\sqrt{4a^2+1}}</math>. Hence, the <math>y</math>-coordinate of <math>E</math> is just <math>\frac{BE\cdot CE}{BC}=\frac{4a}{4a^2+1}</math>. Since <math>E</math> lies on the unit circle, we can compute the <math>x</math> coordinate as <math>\frac{1-4a^2}{4a^2+1}</math>. By Shoelace, we want <cmath>\frac{1}{2}\det\begin{bmatrix}
+-1 & 4a & 1\\
+\frac{1-4a^2}{4a^2+1} & \frac{4a}{4a^2+1} & 1\\
+& \frac{1}{a} & 1
+\end{bmatrix}=17\cdot\frac{1}{2}\cdot 2 \cdot \frac{4a}{4a^2+1}</cmath>Factoring out denominators and expanding by minors, this is equivalent to
+<cmath>\frac{32a^4-8a^2+2}{2a(4a^2+1)}=\frac{68a}{4a^2+1} \Longrightarrow 16a^4-72a^2+1=0</cmath>This factors as <math>(4a^2-8a-1)(4a^2+8a-1)=0</math>, so <math>a=1+\frac{\sqrt{5}}{2}</math> and so the answer is <math> \textbf{(D) \ }</math>.
+==Solution 5==
+Let <math>C = (0,0), D=(\frac1a, 0), B = (0,1), A = (a,1)</math> where <math>a>1</math>. Because <math>BC = 1, a = \frac{AB}{BC}</math>. Notice that the diagonals are perpendicular with slopes of <math>\frac1a</math> and <math>-a</math>. Let the intersection of <math>AC</math> and <math>BD</math> be <math>F</math>, then <math>\triangle BFC \sim \triangle ABC</math>. However, because <math>ABCD</math> is a trapezoid, <math>\triangle</math><math>BCF</math> and <math>\triangle ADF</math> share the same area, therefore <math>\triangle</math><math>BCE</math> is the reflection of <math>\triangle</math><math>BCF</math> over the perpendicular bisector of <math>BC</math>, which is <math>y=\frac12</math>. We use the linear equations of the diagonals, <math>y = -ax + 1, y = \frac1a x</math>, to find the coordinates of <math>F</math>. <cmath>-ax+1 = \frac1ax \Longrightarrow x = \frac{1}{a+\frac1a} = \frac{a}{a^2+1}</cmath> <cmath>y = \frac1ax = \frac{1}{a^2+1}</cmath>
+The y-coordinate of <math>E</math> is simply <math>1-\frac{1}{a^2+1} = \frac{a^2}{a^2+1}</math>
+The area of <math>\triangle BCE</math> is <math>\frac12 \frac{a}{a^2+1}</math>. We apply shoelace theorem to solve for the area of <math>\triangle ADE</math>. The coordinates of the triangle are <math>\{(\frac{a}{a^2+1}, \frac{a^2}{a^2+1}), (a,1), (\frac1a, 0)\}</math>, so the area is
+<cmath>\frac12 |\frac{a^3}{a^2+1} + \frac1a - \frac{a}{a^2+1} - \frac{a}{a^2+1}| = \frac12 |\frac{a^3-2a}{a^2+1} + \frac1a|</cmath>
+<cmath>= \frac12 |\frac{a^4-2a^2}{a(a^2+1)} + \frac{a^2+1}{a(a^2+1)}| = \frac12 \frac{a^4-a^2+1}{a(a^2+1)}</cmath>
+Finally, we use the property that the ratio of areas equals <math>17</math> <cmath>\frac{\frac12}{\frac12} \frac{\frac{a^4-a^2+1}{a(a^2+1)}}{\frac{a}{a^2+1}} = 17 \Rightarrow \frac{a^4-a^2+1}{a^2} = 17 \Rightarrow a^4-18a^2+1 = 0</cmath>
+<cmath>a^2 = 9+4\sqrt{5} = (2+\sqrt{5})^2 \Longrightarrow a = \boxed{\textbf{(D) } 2+\sqrt{5}}</cmath>
+~Zeric
+==Solution 6==
+This solution involves proving <math>\triangle AED \sim \triangle CEB</math>.
+Let <math>E'</math> be the intersection of <math>AC</math> and <math>BD</math>. Label points <math>F</math> and <math>G</math> the same way as <math>\textbf{Solution 3}</math>.
+<math>\angle AE'D = \angle CE'B = \frac{\pi}{2} = \angle AFE</math>. Additionally, <math>\frac{E'D}{FE} = \frac{E'D}{E'G} = \frac{AE'}{AF}</math>, so <math>\triangle AFE \sim \triangle AE'D</math> by SAS. Therefore, <math>\angle BAC = \angle FAE + \angle EAE' = \angle E'AD + \angle EAE' = \angle EAD</math>.
+Next, <math>\angle AFE = \frac{\pi}{2} = \angle EGD</math> because <math>FG \parallel BC</math>. Also, <math>\pi = \angle FEA + \angle AED + \angle DEG = \angle FEA + \angle AED + \angle EAF = \frac{\pi}{2} + \angle AED</math>, so <math>\angle AED = \frac{\pi}{2}</math>. Therefore, <math>\triangle AED \sim \triangle ABC</math> by AA. Since <math>\triangle CEB \sim \triangle ABC</math>, <math>\triangle AED \sim \triangle CEB</math>.
+Given <math>\frac{[AED]}{[CEB]} = 17</math>, we deduce that the ratio of corresponding side lengths of <math>AED</math> to <math>CEB</math> must be <math>\sqrt{17}</math>. Now, we set <math>BC = 1</math>, <math>AB = x</math>, and <math>CD = \frac{1}{x}</math>. Using the Pythagorean Theorem, <math>AD = \sqrt{\Big(x-\frac{1}{x}\Big)^2 + 1^2}</math>. Thus, <math>\sqrt{17} = \frac{AD}{CB} = \frac{\sqrt{\Big(x-\frac{1}{x}\Big)^2 + 1^2}}{1}</math>. Solving gives <math>x = 2+\sqrt{5}</math>.
+Finally, <math>\frac{AB}{BC} = \frac{2+\sqrt{5}}{1} = \boxed{\textbf{(D) } 2+\sqrt{5}}</math>.
+~Zhixing
+==Video Solution by MOP 2024==
+https://youtu.be/h92s2BxlohI
+~r00tsOfUnity
+== Notes==
+) <math>\sqrt{17}</math> is the most relevant answer choice because it shares numbers with the givens of the problem.
+) It's a very good guess to replace finding the area of triangle AED with the area of the triangle DAF, where F is the projection of D onto AB(then find the closest answer choice).
 ==See Also==
 {{AMC12 box|year=2017|ab=B|num-b=23|num-a=25}}
 {{MAA Notice}}
+[[Category:Intermediate Geometry Problems]]

2017 AMC 12B (Problems • Answer Key • Resources)
Preceded by Problem 23	Followed by Problem 25
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

Page

Toolbox

Search