Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2007 AMC 12B Problems/Problem 25"

(→‎Solution)
(→‎Solution 1)
 
(8 intermediate revisions by 4 users not shown)
Line 4: Line 4:
 
<math>\mathrm {(A)} \sqrt{2}\qquad \mathrm {(B)} \sqrt{3}\qquad \mathrm {(C)} 2\qquad \mathrm {(D)} \sqrt{5}\qquad \mathrm {(E)} \sqrt{6}</math>
 
<math>\mathrm {(A)} \sqrt{2}\qquad \mathrm {(B)} \sqrt{3}\qquad \mathrm {(C)} 2\qquad \mathrm {(D)} \sqrt{5}\qquad \mathrm {(E)} \sqrt{6}</math>
  
−
==Solution==
+
==Solution 1==
 +
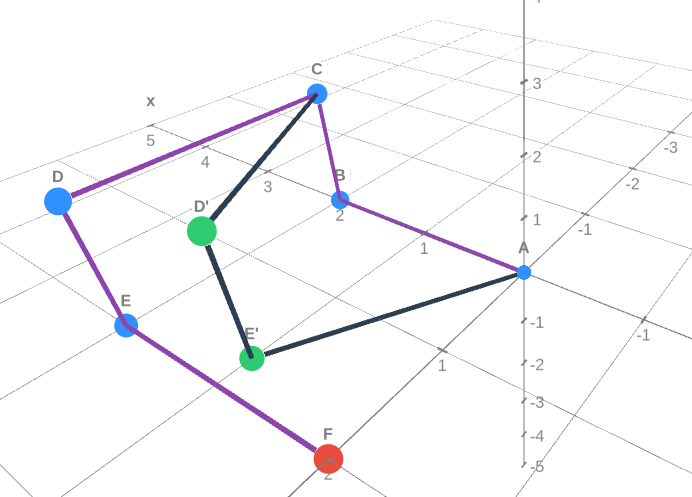
[[File:2007 AMC 12B Problem 25.png|center]]
 +
Link to graph: https://www.math3d.org/pHFSD6vRi
 +
 
 +
 
 
Let <math>A=(0,0,0)</math>, and <math>B=(2,0,0)</math>. Since <math>EA=2</math>, we could let <math>C=(2,0,2)</math>, <math>D=(2,2,2)</math>, and <math>E=(2,2,0)</math>. Now to get back to <math>A</math> we need another vertex <math>F=(0,2,0)</math>. Now if we look at this configuration as if it was two dimensions, we would see a square missing a side if we don't draw <math>FA</math>. Now we can bend these three sides into an equilateral triangle, and the coordinates change: <math>A=(0,0,0)</math>, <math>B=(2,0,0)</math>, <math>C=(2,0,2)</math>, <math>D=(1,\sqrt{3},2)</math>, and <math>E=(1,\sqrt{3},0)</math>. Checking for all the requirements, they are all satisfied. Now we find the area of triangle <math>BDE</math>. The side lengths of this triangle are <math>2, 2, 2\sqrt{2}</math>, which is an isosceles right triangle. Thus the area of it is <math>\frac{2\cdot2}{2}=2\Rightarrow \mathrm{(C)}</math>.
 
Let <math>A=(0,0,0)</math>, and <math>B=(2,0,0)</math>. Since <math>EA=2</math>, we could let <math>C=(2,0,2)</math>, <math>D=(2,2,2)</math>, and <math>E=(2,2,0)</math>. Now to get back to <math>A</math> we need another vertex <math>F=(0,2,0)</math>. Now if we look at this configuration as if it was two dimensions, we would see a square missing a side if we don't draw <math>FA</math>. Now we can bend these three sides into an equilateral triangle, and the coordinates change: <math>A=(0,0,0)</math>, <math>B=(2,0,0)</math>, <math>C=(2,0,2)</math>, <math>D=(1,\sqrt{3},2)</math>, and <math>E=(1,\sqrt{3},0)</math>. Checking for all the requirements, they are all satisfied. Now we find the area of triangle <math>BDE</math>. The side lengths of this triangle are <math>2, 2, 2\sqrt{2}</math>, which is an isosceles right triangle. Thus the area of it is <math>\frac{2\cdot2}{2}=2\Rightarrow \mathrm{(C)}</math>.
 +
 +
==Solution 2==
 +
 +
Similar to solution 1, we allow
 +
<math>A=(0,0,0)</math>, <math>B=(2,0,0)</math>, and <math>C=(0,2,0)</math>. This creates the isosceles right triangle on the plane of <math>z=0</math>
 +
 +
Now, note that <math>\angle CDE=\angle DEA=90^o</math>. This means that there exists some vector <math>DE</math> parallel to the plane of <math>ABC</math> that forms two right angles with <math>AE</math> and <math>CD</math>. By definition, this is the cross product of the two vectors <math>AE</math> and <math>CD</math>. Finding this cross product, we take the determinant of vectors
 +
 +
<math>AE=<x_1,y_1,z></math> and
 +
 +
<math>CD=<x_2,y_2,z></math> *Note that z is constant because the line is parallel to the plane*
 +
 +
to get <math>(y_1-y_2)zi+(x_1-x_2)zj+(x_1y_2-y_1x_2)k</math>
 +
 +
Because there can be no movement in the <math>z</math> direction, the k unit vector must be zero. Also, because the i unit vector must be orthogonal and also 0. Thus, the vector of line <math>DE</math> is simply <math>2tj+2k</math>
 +
 +
From this, you can figure out that line <math>BE=2</math>, and the area of <math>BDE=\frac{2\cdot2}{2}=2\Rightarrow \mathrm{(C)}</math>.
  
 
==See also==
 
==See also==

Latest revision as of 18:46, 17 July 2023

Problem

Points $A,B,C,D$ and $E$ are located in 3-dimensional space with $AB=BC=CD=DE=EA=2$ and $\angle ABC=\angle CDE=\angle DEA=90^o$. The plane of $\triangle ABC$ is parallel to $\overline{DE}$. What is the area of $\triangle BDE$?

$\mathrm {(A)} \sqrt{2}\qquad \mathrm {(B)} \sqrt{3}\qquad \mathrm {(C)} 2\qquad \mathrm {(D)} \sqrt{5}\qquad \mathrm {(E)} \sqrt{6}$

Solution 1

2007 AMC 12B Problem 25.png

Link to graph: https://www.math3d.org/pHFSD6vRi


Let $A=(0,0,0)$, and $B=(2,0,0)$. Since $EA=2$, we could let $C=(2,0,2)$, $D=(2,2,2)$, and $E=(2,2,0)$. Now to get back to $A$ we need another vertex $F=(0,2,0)$. Now if we look at this configuration as if it was two dimensions, we would see a square missing a side if we don't draw $FA$. Now we can bend these three sides into an equilateral triangle, and the coordinates change: $A=(0,0,0)$, $B=(2,0,0)$, $C=(2,0,2)$, $D=(1,\sqrt{3},2)$, and $E=(1,\sqrt{3},0)$. Checking for all the requirements, they are all satisfied. Now we find the area of triangle $BDE$. The side lengths of this triangle are $2, 2, 2\sqrt{2}$, which is an isosceles right triangle. Thus the area of it is $\frac{2\cdot2}{2}=2\Rightarrow \mathrm{(C)}$.

Solution 2

Similar to solution 1, we allow $A=(0,0,0)$, $B=(2,0,0)$, and $C=(0,2,0)$. This creates the isosceles right triangle on the plane of $z=0$

Now, note that $\angle CDE=\angle DEA=90^o$. This means that there exists some vector $DE$ parallel to the plane of $ABC$ that forms two right angles with $AE$ and $CD$. By definition, this is the cross product of the two vectors $AE$ and $CD$. Finding this cross product, we take the determinant of vectors

$AE=<x_1,y_1,z>$ and

$CD=<x_2,y_2,z>$ *Note that z is constant because the line is parallel to the plane*

to get $(y_1-y_2)zi+(x_1-x_2)zj+(x_1y_2-y_1x_2)k$

Because there can be no movement in the $z$ direction, the k unit vector must be zero. Also, because the i unit vector must be orthogonal and also 0. Thus, the vector of line $DE$ is simply $2tj+2k$

From this, you can figure out that line $BE=2$, and the area of $BDE=\frac{2\cdot2}{2}=2\Rightarrow \mathrm{(C)}$.

See also

2007 AMC 12B (Problems • Answer Key • Resources)
Preceded by
Problem 24 		Followed by
Last Problem
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2007_AMC_12B_Problems/Problem_25&oldid=195841"