Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2010 AMC 10B Problems/Problem 20"

m (→‎Solution 1)
m (→‎Solution 2)
 
(12 intermediate revisions by 6 users not shown)
Line 6: Line 6:
  
 
== Solution 1 ==
 
== Solution 1 ==
−
A good diagram is very helpful. Also, BC and FA are LINES, not LINE SEGMENTS.
+
A good diagram is very helpful.  
  
 
<center> [[File:Amc10B 2010.gif]] </center>
 
<center> [[File:Amc10B 2010.gif]] </center>
Line 18: Line 18:
  
 
== Solution 2 ==
 
== Solution 2 ==
−
As above, we note that the first circle is inscribed in an equilateral triangle of sidelength 1 (if we assume, WLOG, that the regular hexagon has sidelength 1). The inradius of an equilateral triangle with sidelength 1 is equal to <math>\frac{\sqrt{3}}{6}</math>. Therefore, the area of the first circle is <math>(\frac{\sqrt{3}}{6})^2 \cdot \pi =\frac{\pi}{12}</math>.
+
As above, we note that the first circle is inscribed in an equilateral triangle of side length <math>1</math> (if we assume, WLOG, that the regular hexagon has side length <math>1</math>). The inradius of an equilateral triangle with side length <math>1</math> is equal to <math>\frac{\sqrt{3}}{6}</math>. Therefore, the area of the first circle is <math>(\frac{\sqrt{3}}{6})^2 \cdot \pi =\frac{\pi}{12}</math>.
  
  
−
Call the center of the second circle <math>O</math>. Now we drop a perpendicular from <math>O</math> to Circle O's point of tangency with <math>GK</math> and draw another line connecting O to G. Note that because triangle <math>BGA</math> is equilateral, <math>\angle BGA=60^{\circ}</math>. <math>OG</math> bisects <math>\angle BGA</math>, so we have a 30-60-90 triangle.  
+
Call the center of the second circle <math>O</math>. Now we drop a perpendicular from <math>O</math> to circle <math>O</math>'s point of tangency with <math>GK</math> and draw another line connecting <math>O</math> to <math>G</math>. Note that because triangle <math>BGA</math> is equilateral, <math>\angle BGA=60^{\circ}</math>. <math>OG</math> bisects <math>\angle BGA</math>, so we have a <math>30-60-90</math> triangle.  
  
  
−
Call the radius of Circle O "<math>r</math>".
+
Call the radius of circle <math>O</math> <math>r</math>.
−
<math>OG=2r</math>= height of equilateral triangle + height of regular hexagon + r
+
<math>OG=2r= \text{height of equilateral triangle} + \text{height of regular hexagon} + r</math>
  
−
The height of an equilateral triangle of sidelength 1 is <math>\frac{\sqrt{3}}{2}</math>. The height of an equilateral hexagon of sidelength 1 is <math>\sqrt{3}</math>. Therefore,
+
The height of an equilateral triangle of side length <math>1</math> is <math>\frac{\sqrt{3}}{2}</math>. The height of a regular hexagon of side length <math>1</math> is <math>\sqrt{3}</math>. Therefore,
 
<math>OG=\frac{\sqrt{3}}{2} + \sqrt{3} + r</math>.
 
<math>OG=\frac{\sqrt{3}}{2} + \sqrt{3} + r</math>.
  
Line 38: Line 38:
 
<math>\frac{3\sqrt{3}}{2}=r</math>
 
<math>\frac{3\sqrt{3}}{2}=r</math>
  
−
The area of Circle O equals <math>\pi r^2=\frac{27}{4} \pi</math>
+
The area of Circle <math>O</math> equals <math>\pi r^2=\frac{27}{4} \pi</math>
  
−
Therefore, the ratio of the areas is <math>\frac{\frac{1}{12}}{\frac{27}{4}}=81</math>
+
Therefore, the ratio of the areas is <math>\frac{\frac{27}{4}}{\frac{1}{12}}=\boxed{\textbf{(D)}\ 81}</math>
 +
 
 +
==Video Solution==
 +
https://youtu.be/FQO-0E2zUVI?t=1381
 +
 
 +
~IceMatrix
  
 
==See Also==
 
==See Also==
 
{{AMC10 box|year=2010|ab=B|num-b=19|num-a=21}}
 
{{AMC10 box|year=2010|ab=B|num-b=19|num-a=21}}
 
{{MAA Notice}}
 
{{MAA Notice}}

Latest revision as of 17:41, 4 May 2024

Problem

Two circles lie outside regular hexagon $ABCDEF$. The first is tangent to $\overline{AB}$, and the second is tangent to $\overline{DE}$. Both are tangent to lines $BC$ and $FA$. What is the ratio of the area of the second circle to that of the first circle?

$\textbf{(A)}\ 18 \qquad \textbf{(B)}\ 27 \qquad \textbf{(C)}\ 36 \qquad \textbf{(D)}\ 81 \qquad \textbf{(E)}\ 108$

Solution 1

A good diagram is very helpful.

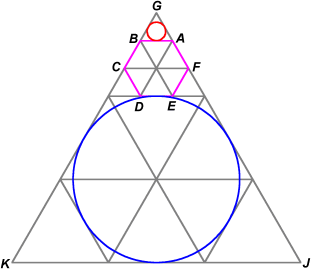
Amc10B 2010.gif

The first circle is in red, the second in blue. With this diagram, we can see that the first circle is inscribed in equilateral triangle $GBA$ while the second circle is inscribed in $GKJ$. From this, it's evident that the ratio of the blue area to the red area is equal to the ratio of the areas $\triangle GKJ$ to $\triangle GBA$

Since the ratio of areas is equal to the square of the ratio of lengths, we know our final answer is $\left(\frac{GK}{GB}\right)^2$. From the diagram, we can see that this is $9^2=\boxed{\textbf{(D)}\ 81}$

Solution 2

As above, we note that the first circle is inscribed in an equilateral triangle of side length $1$ (if we assume, WLOG, that the regular hexagon has side length $1$). The inradius of an equilateral triangle with side length $1$ is equal to $\frac{\sqrt{3}}{6}$. Therefore, the area of the first circle is $(\frac{\sqrt{3}}{6})^2 \cdot \pi =\frac{\pi}{12}$.


Call the center of the second circle $O$. Now we drop a perpendicular from $O$ to circle $O$'s point of tangency with $GK$ and draw another line connecting $O$ to $G$. Note that because triangle $BGA$ is equilateral, $\angle BGA=60^{\circ}$. $OG$ bisects $\angle BGA$, so we have a $30-60-90$ triangle.


Call the radius of circle $O$ $r$. $OG=2r= \text{height of equilateral triangle} + \text{height of regular hexagon} + r$

The height of an equilateral triangle of side length $1$ is $\frac{\sqrt{3}}{2}$. The height of a regular hexagon of side length $1$ is $\sqrt{3}$. Therefore, $OG=\frac{\sqrt{3}}{2} + \sqrt{3} + r$.

We can now set up the following equation:

$\frac{\sqrt{3}}{2} + \sqrt{3} + r=2r$

$\frac{\sqrt{3}}{2} + \sqrt{3}=r$

$\frac{3\sqrt{3}}{2}=r$

The area of Circle $O$ equals $\pi r^2=\frac{27}{4} \pi$

Therefore, the ratio of the areas is $\frac{\frac{27}{4}}{\frac{1}{12}}=\boxed{\textbf{(D)}\ 81}$

Video Solution

https://youtu.be/FQO-0E2zUVI?t=1381

~IceMatrix

See Also

2010 AMC 10B (Problems • Answer Key • Resources)
Preceded by
Problem 19 		Followed by
Problem 21
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2010_AMC_10B_Problems/Problem_20&oldid=219005"