Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Pythagoras Theorem"

(→‎Pythagorean Triples)
(→‎Pythagorean Triples)
Line 92: Line 92:
 
<math>(a+b)^2=c^2+4\left(\frac{1}{2}ab\right)\implies a^2+2ab+b^2=c^2+2ab\implies a^2 + b^2=c^2</math>. {{Halmos}}
 
<math>(a+b)^2=c^2+4\left(\frac{1}{2}ab\right)\implies a^2+2ab+b^2=c^2+2ab\implies a^2 + b^2=c^2</math>. {{Halmos}}
 
== Pythagorean Triples ==
 
== Pythagorean Triples ==
 +
Pythagorean Triples are a group of integers a,b and c in which <math>a^2+b^2=c^2</math>. These are the first few:
 
(3,4,5) (5,12,13) (7,24,25) (8,15,17)
 
(3,4,5) (5,12,13) (7,24,25) (8,15,17)
 
(9,40,41) (11,60,61) (12,35,37) (13,84,85)
 
(9,40,41) (11,60,61) (12,35,37) (13,84,85)
Line 100: Line 101:
 
(33,56,65) (33,544,545) (35,612,613) (36,77,85)
 
(33,56,65) (33,544,545) (35,612,613) (36,77,85)
 
(36,323,325) (37,684,685) And on and on...
 
(36,323,325) (37,684,685) And on and on...
−
Remember that if <math>a^2+b^2=c^2</math> then <math>xa^2+xb^2=xc^2</math>
+
Remember that if <math>a^2+b^2=c^2</math> then <math>xa^2+xb^2=xc^2</math> so I did not include 6,8,10 or 10,24,26.

Revision as of 17:21, 17 June 2019

What is the Pythagorean Theorem?

What is the Pythagorean Theorem?

The Pythagoras Theorem is also referred to as the Pythagorean Theorem$.$ Pythagorean Theorem is used to find a side of any right triangle. It is $a^2+b^2=c^2$, where $a$ and $b$ are the legs of the triangle, and $c$ is the hypotenuse.

Why is it useful?

To find sides and angles of right triangles. Also, Trigonometry is pointless without it. If you know three angles of a triangle you can use the Pythagorean Theorem to find the sides or the area even if the angles are not right. It is probably the most famous Theorem in all of math!

Can we prove it?

Yes! The are hundreds of proves. I will just show you a few of them. Mathematicians even make a hobby of finding these proves. Even a US president made a published proof! Of, course this was a president in the 1800s because, well, presidents now are not really up to proving something like that. (You know, Trump and the others).

Proofs

Proof 1

We use $[ABC]$ to denote the area of triangle $ABC$.

Let $H$ be the perpendicular to side $AB$ from ${} C$.

[asy] pair A, B, C, H; A = (0, 0); B = (4, 3); C = (4, 0); H = foot(C, A, B); draw(A--B--C--cycle); draw(C--H); draw(rightanglemark(A, C, B)); draw(rightanglemark(C, H, B)); label("$A$", A, SSW); label("$B$", B, ENE); label("$C$", C, SE); label("$H$", H, NNW); [/asy]

Since $ABC, CBH, ACH$ are similar right triangles, and the areas of similar triangles are proportional to the squares of corresponding side lengths,

$\frac{[ABC]}{AB^2} = \frac{[CBH]}{CB^2} = \frac{[ACH]}{AC^2}$.

But since triangle $ABC$ is composed of triangles $CBH$ and $ACH$, $[ABC] = [CBH] + [ACH]$, so $AB^2 = CB^2 + AC^2$. ∎

Proof 2

Consider a circle $\omega$ with center $B$ and radius $BC$. Since $BC$ and $AC$ are perpendicular, $AC$ is tangent to $\omega$. Let the line $AB$ meet $\omega$ at $Y$ and $X$, as shown in the diagram:

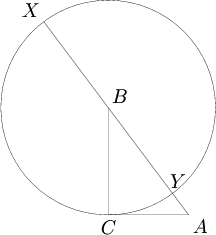
Pyth2.png

Evidently, $AY = AB - BC$ and $AX = AB + BC$. By considering the power of point $A$ with respect to $\omega$, we see

$AC^2 = AY \cdot AX = (AB-BC)(AB+BC) = AB^2 - BC^2$. ∎

Proof 3

$ABCD$ and $EFGH$ are squares.

[asy] pair A, B,C,D; A = (-10,10); B = (10,10); C = (10,-10); D = (-10,-10); pair E,F,G,H; E = (7,10); F = (10, -7); G = (-7, -10); H = (-10, 7); draw(A--B--C--D--cycle); label("$A$", A, NNW); label("$B$", B, ENE); label("$C$", C, ESE); label("$D$", D, SSW); draw(E--F--G--H--cycle); label("$E$", E, N); label("$F$", F,SE); label("$G$", G, S); label("$H$", H, W); label("a", A--B,N); label("a", B--F,SE); label("a", C--G,S); label("a", H--D,W); label("b", E--B,N); label("b", F--C,SE); label("b", G--D,S); label("b", A--H,W); label("c", E--H,NW); label("c", E--F); label("c", F--G,SE); label("c", G--H,SW); [/asy]

$(a+b)^2=c^2+4\left(\frac{1}{2}ab\right)\implies a^2+2ab+b^2=c^2+2ab\implies a^2 + b^2=c^2$. ∎

Pythagorean Triples

Pythagorean Triples are a group of integers a,b and c in which $a^2+b^2=c^2$. These are the first few: (3,4,5) (5,12,13) (7,24,25) (8,15,17) (9,40,41) (11,60,61) (12,35,37) (13,84,85) (15,112,113) (16,63,65) (17,144,145) (19,180,181) (20,21,29) (20,99,101) (21,220,221) (23,264,265) (24,143,145) (25,312,313) (27,364,365) (28,45,53) (28,195,197) (29,420,421) (31,480,481) (32,255,257) (33,56,65) (33,544,545) (35,612,613) (36,77,85) (36,323,325) (37,684,685) And on and on... Remember that if $a^2+b^2=c^2$ then $xa^2+xb^2=xc^2$ so I did not include 6,8,10 or 10,24,26.

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Pythagoras_Theorem&oldid=106536"