Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2020 AIME I Problems/Problem 1"

(Created page with "== Problem == Let <math>ABCD</math> be a parallelogram. Extend <math>\overline{DA}</math> through <math>A</math> to a point <math>P,</math> and let <math>\overline{PC}</m...")
 
(→‎Solution 2)
Line 33: Line 33:
 
=== Solution 2 ===
 
=== Solution 2 ===
  
−
We have <math>\triangle BRQ\sim \triangle DRC</math> so <math>\frac{112}{RC} = \frac{BR}{DR}</math>. We also have <math>\triangle BRC \sim \triangle DRP</math> so <math>\frac{ RC}{847} = \frac {BR}{DR}</math>. Equating the two results gives <math>\frac{112}{RC} =  \frac{ RC}{847}</math> and so <math>RC^2=112*847</math> which solves to <math>RC=\boxed{308}</math>
+
We have <math>\triangle BRQ\sim \triangle DRC</math> so <math>\frac{112}{RC} = \frac{BR}{DR}</math>. We also have <math>\triangle BRC \sim \triangle DRP</math> so <math>\frac{ RC}{847} = \frac {BR}{DR}</math>. Equating the two results gives <math>\frac{112}{RC} =  \frac{ RC}{847}</math> and so <math>RC^2=112*847</math> which solves to <math>RC=\boxed{481}</math>

Revision as of 15:56, 27 February 2020

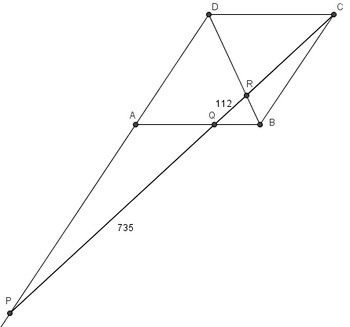
Problem

Let $ABCD$ be a parallelogram. Extend $\overline{DA}$ through $A$ to a point $P,$ and let $\overline{PC}$ meet $\overline{AB}$ at $Q$ and $\overline{DB}$ at $R.$ Given that $PQ = 735$ and $QR = 112,$ find $RC.$

Solution

Solution 1

AIME 1998-6.png

There are several similar triangles. $\triangle PAQ\sim \triangle PDC$, so we can write the proportion:

$\frac{AQ}{CD} = \frac{PQ}{PC} = \frac{735}{112 + 735 + RC} = \frac{735}{847 + RC}$

Also, $\triangle BRQ\sim DRC$, so:

$\frac{QR}{RC} = \frac{QB}{CD} = \frac{112}{RC} = \frac{CD - AQ}{CD} = 1 - \frac{AQ}{CD}$

$\frac{AQ}{CD} = 1 - \frac{112}{RC} = \frac{RC - 112}{RC}$

Substituting,

$\frac{AQ}{CD} = \frac{735}{847 + RC} = \frac{RC - 112}{RC}$

$735RC = (RC + 847)(RC - 112)$
$0 = RC^2 - 112\cdot847$

Thus, $RC = \sqrt{112*847} = 308$.

Solution 2

We have $\triangle BRQ\sim \triangle DRC$ so $\frac{112}{RC} = \frac{BR}{DR}$. We also have $\triangle BRC \sim \triangle DRP$ so $\frac{ RC}{847} = \frac {BR}{DR}$. Equating the two results gives $\frac{112}{RC} = \frac{ RC}{847}$ and so $RC^2=112*847$ which solves to $RC=\boxed{481}$

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2020_AIME_I_Problems/Problem_1&oldid=118488"