Difference between revisions of "2020 AIME I Problems/Problem 1"
(→Solution 1) |
(→Solution 1) |
||
| Line 29: | Line 29: | ||
</div> | </div> | ||
| − | Thus, <math> RC = \sqrt{13*17797} = | + | Thus, <math> RC = \sqrt{13*17797} = 481</math>. |
=== Solution 2 === | === Solution 2 === | ||
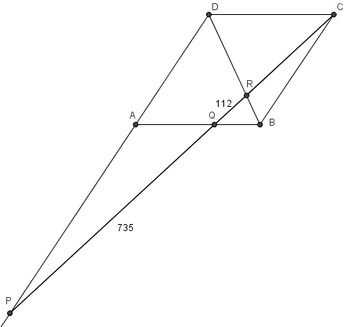
We have <math>\triangle BRQ\sim \triangle DRC</math> so <math>\frac{112}{RC} = \frac{BR}{DR}</math>. We also have <math>\triangle BRC \sim \triangle DRP</math> so <math>\frac{ RC}{847} = \frac {BR}{DR}</math>. Equating the two results gives <math>\frac{13}{RC} = \frac{ RC}{17797}</math> and so <math>RC^2=13*17797</math> which solves to <math>RC=\boxed{481}</math> | We have <math>\triangle BRQ\sim \triangle DRC</math> so <math>\frac{112}{RC} = \frac{BR}{DR}</math>. We also have <math>\triangle BRC \sim \triangle DRP</math> so <math>\frac{ RC}{847} = \frac {BR}{DR}</math>. Equating the two results gives <math>\frac{13}{RC} = \frac{ RC}{17797}</math> and so <math>RC^2=13*17797</math> which solves to <math>RC=\boxed{481}</math> | ||
Revision as of 16:59, 27 February 2020
Contents
[hide]Problem
Let ![]() be a parallelogram. Extend
be a parallelogram. Extend ![]() through
through ![]() to a point
to a point ![]() and let
and let ![]() meet
meet ![]() at
at ![]() and
and ![]() at
at ![]() Given that
Given that ![]() and
and ![]() find
find ![]()
Solution
Solution 1
There are several similar triangles. ![]() , so we can write the proportion:
, so we can write the proportion:
![]()
Also, ![]() , so:
, so:
![]()
![]()
Substituting,
![]()
![]()
![]()
Thus, ![]() .
.
Solution 2
We have ![]() so
so ![]() . We also have
. We also have ![]() so
so ![]() . Equating the two results gives
. Equating the two results gives ![]() and so
and so ![]() which solves to
which solves to ![]()