Difference between revisions of "1997 PMWC Problems/Problem I15"

Revision as of 17:16, 8 October 2007

How many paths from A to B consist of exactly six line segments (vertical, horizontal or inclined)?

Ignoring the diagonal segments, there are $\frac{6!}{3!3!} = 20$ paths.
Traversing the diagonals, we quickly find that the path must run through exactly 2 diagonals. There are ${3\choose2} = 3$ pairs of diagonals through which this is possible; quick counting shows us that each pair of diagonals yields 2 paths. So there are 6 more cases here.

In total, we get $20 + 6 = 26$ paths.

@@ Line 1: / Line 1: @@
+== Problem ==
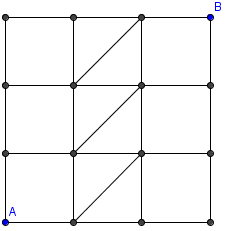
+How many paths from A to B consist of exactly six line
+segments (vertical, horizontal or inclined)?
+[[Image:1997_PMWC-I15.png]]
+== Solution ==
+[[Casework]]:
+*Ignoring the diagonal segments, there are <math>\frac{6!}{3!3!} = 20</math> paths.
+*Traversing the diagonals, we quickly find that the path must run through exactly 2 diagonals. There are <math>{3\choose2} = 3</math> pairs of diagonals through which this is possible; quick counting shows us that each pair of diagonals yields 2 paths. So there are 6 more cases here.
+In total, we get <math>20 + 6 = 26</math> paths.
+== See also ==
+{{PMWC box|year=1997|num-b=I14|num-a=T1}}
+[[Category:Introductory Combinatorics Problems]]