Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1991 OIM Problems/Problem 6"
Line 14: Line 14:
  
 
'''Case 2:''' <math>\angle NHM \ne 90^{\circ}</math>
 
'''Case 2:''' <math>\angle NHM \ne 90^{\circ}</math>
 +
 +
[[File:1991_OIM_P6b.png|500px]]
 +
 +
Let the red circle in the image above be the circumcircle of triangle <math>ABC</math>.  Let <math>BD</math> be a diameter of the circle.  This means that <math>\angle BAD</math> and <math>\angle BCD</math> are both equal to <math>90^{\circ}</math> because right angle triangles inscribed in circles with the hypothenuse on the diameter.  Therefore <math>AH</math> is parallel to <math>DC</math> and <math>CH</math> is parallel to <math>CD</math>.  Thus quadrilateral <math>ADCH</math> is a parallelogram with <math>N</math> in the center and <math>HN=ND</math>. So, one can draw point <math>D</math> using <math>N</math> and <math>H</math>.  Since <math>\angle MAD=90^{\circ}</math>, then <math>MD</math> is the diameter of a circle that also passes through <math>A</math>.  This means that one can find point <math>A</math> from the intersection of this circle and the perpendicular to <math>MN</math> that passes through <math>A</math> and we can now start our construction as follows:
 +
  
  

Revision as of 18:21, 22 December 2023

Problem

Given 3 non-aligned points $M$, $N$ and $H$, we know that $M$ and $N$ are midpoints of two sides of a triangle and that $H$ is the point of intersection of the heights of said triangle. Build the triangle.

~translated into English by Tomas Diaz. ~orders@tomasdiaz.com

Solution

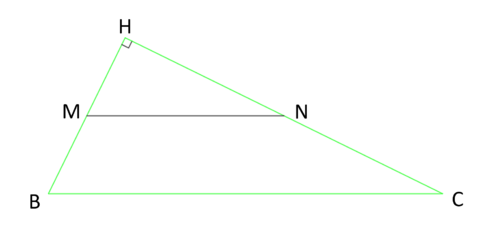
Case 1: $\angle NHM = 90^{\circ}$

1991 OIM P6a.png

If you measure $\angle NHM$ on the given points and it happens to be a right angle, then constructing the triangle is easy because point $H$ is also point $A$ of the triangle $ABC$. One can notice if this angle is a right angle or not if you can draw a perpendicular from point $M$ to line $NH$ and it passes through $H$. If this happens to be the case, then since $AM=MB$ and $AN=NC$ then one can simply draw a circle with the compass at points $M$ and $N$ with radiuses measuring $MA$ and $NA$ respectively. Then extend the lines $AM$ and $AN$ to the intersection on their respective circles at $B$ and $C$ respectively. Then draw triangle $ABC$.


Case 2: $\angle NHM \ne 90^{\circ}$

1991 OIM P6b.png

Let the red circle in the image above be the circumcircle of triangle $ABC$. Let $BD$ be a diameter of the circle. This means that $\angle BAD$ and $\angle BCD$ are both equal to $90^{\circ}$ because right angle triangles inscribed in circles with the hypothenuse on the diameter. Therefore $AH$ is parallel to $DC$ and $CH$ is parallel to $CD$. Thus quadrilateral $ADCH$ is a parallelogram with $N$ in the center and $HN=ND$. So, one can draw point $D$ using $N$ and $H$. Since $\angle MAD=90^{\circ}$, then $MD$ is the diameter of a circle that also passes through $A$. This means that one can find point $A$ from the intersection of this circle and the perpendicular to $MN$ that passes through $A$ and we can now start our construction as follows:



  • Note. I actually competed at this event in Argentina when I was in High School representing Puerto Rico. I think I may have been able to build some cases of this. I don't remember much of it.

Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.

See also

https://www.oma.org.ar/enunciados/ibe6.htm

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1991_OIM_Problems/Problem_6&oldid=208136"