Difference between revisions of "2016 IMO Problems/Problem 1"
(→Solution) |
m (→Solution 2) |
||
| Line 18: | Line 18: | ||
== Solution 2 == | == Solution 2 == | ||
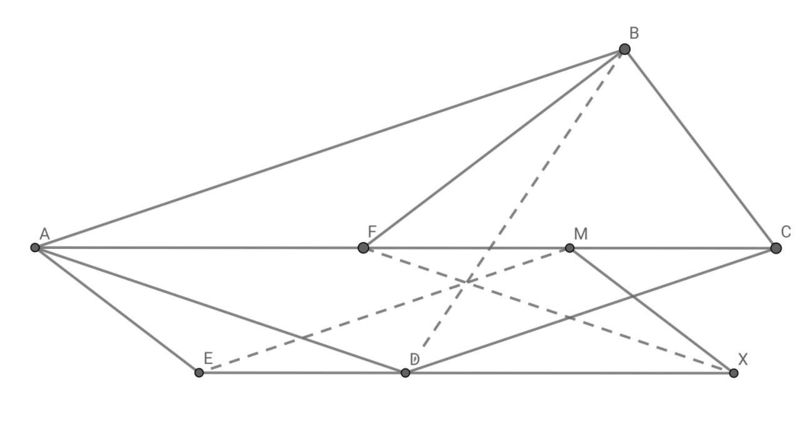
| − | Let <math>\angle(FBA) = \angle(FAB) = \angle(FAD) = \angle(FCD) = \alpha</math>. And WLOG, <math>MF = 1</math>. Hence, <math>CF = 2</math>, <math>BF = 2.cos(2\alpha) = FA</math>, <math>DA = AC | + | Let <math>\angle(FBA) = \angle(FAB) = \angle(FAD) = \angle(FCD) = \alpha</math>. And WLOG, <math>MF = 1</math>. Hence, <math>CF = 2</math>, <math>BF = 2.cos(2\alpha) = FA</math>, <math>DA = {AC}{2cos(\alpha)} = {1+cos(2\alpha}{cos(\alpha)}</math> and <math>DE = AE = {AD}{2cos(\alpha)} = {1+cos(2\alpha)}{2.(cos(\alpha))^2} = 1</math>. So <math>MX = 1</math> which means <math>B</math>, <math>C</math>, <math>X</math> and <math>F</math> are concyclic. We know that <math>DE // MC</math> and <math>DE = 1 = MC</math>, so we conclude <math>MCDE</math> is parallelogram. So <math>\angle(AME) = \alpha</math>. That means <math>MDEA</math> is isosceles trapezoid. Hence, <math>MD = EA = 1</math>. By basic angle chasing, <math>\angle(MBF) = \angle(MFB) = 2\alpha</math> and <math>\angle(MXD) = \angle(MDX) = 2\alpha</math> and we have seen that <math>MB = MF = MD = MX</math>, so <math>BFDX</math> is isosceles trapezoid. And we know that <math>ME</math> bisects <math>\angle(FMD)</math> so <math>ME</math> is the symmetrical axis of <math>BFDX</math>. İt is clear that the symmetry of <math>BD</math> with respect to <math>ME</math> is <math>FX</math>. And we are done <math>\blacksquare</math>. |
~EgeSaribas | ~EgeSaribas | ||
Revision as of 11:46, 19 May 2024
Contents
[hide]Problem
Triangle ![]() has a right angle at
has a right angle at ![]() . Let
. Let ![]() be the point on line
be the point on line ![]() such that
such that ![]() and
and ![]() lies between
lies between ![]() and
and ![]() . Point
. Point ![]() is chosen so that
is chosen so that ![]() and
and ![]() is the bisector of
is the bisector of ![]() . Point
. Point ![]() is chosen so that
is chosen so that ![]() and
and ![]() is the bisector of
is the bisector of ![]() . Let
. Let ![]() be the midpoint of
be the midpoint of ![]() . Let
. Let ![]() be the point such that
be the point such that ![]() is a parallelogram. Prove that
is a parallelogram. Prove that ![]() and
and ![]() are concurrent.
are concurrent.
Solution
The Problem shows that
And
Finally
~Athmyx
Solution 2
Let ![]() . And WLOG,
. And WLOG, ![]() . Hence,
. Hence, ![]() ,
, ![]() ,
, ![]() and
and ![]() . So
. So ![]() which means
which means ![]() ,
, ![]() ,
, ![]() and
and ![]() are concyclic. We know that
are concyclic. We know that ![]() and
and ![]() , so we conclude
, so we conclude ![]() is parallelogram. So
is parallelogram. So ![]() . That means
. That means ![]() is isosceles trapezoid. Hence,
is isosceles trapezoid. Hence, ![]() . By basic angle chasing,
. By basic angle chasing, ![]() and
and ![]() and we have seen that
and we have seen that ![]() , so
, so ![]() is isosceles trapezoid. And we know that
is isosceles trapezoid. And we know that ![]() bisects
bisects ![]() so
so ![]() is the symmetrical axis of
is the symmetrical axis of ![]() . İt is clear that the symmetry of
. İt is clear that the symmetry of ![]() with respect to
with respect to ![]() is
is ![]() . And we are done
. And we are done ![]() .
.
~EgeSaribas
See Also
| 2016 IMO (Problems) • Resources | ||
| Preceded by First Problem |
1 • 2 • 3 • 4 • 5 • 6 | Followed by Problem 2 |
| All IMO Problems and Solutions | ||