Difference between revisions of "2024 AMC 12B Problems/Problem 21"

Revision as of 09:00, 19 December 2024

Problem

The measures of the smallest angles of three different right triangles sum to $90^\circ$ . All three triangles have side lengths that are primitive Pythagorean triples. Two of them are $3-4-5$ and $5-12-13$ . What is the perimeter of the third triangle?

$\textbf{(A) } 40 \qquad\textbf{(B) } 126 \qquad\textbf{(C) } 154 \qquad\textbf{(D) } 176 \qquad\textbf{(E) } 208$

Solution 1

Let $\alpha$ and $\beta$ be the smallest angles of the $3-4-5$ and $5-12-13$ triangles respectively. We have $\tan(\alpha)=\frac{3}{4} \text{ and } \tan(\beta)=\frac{5}{12}$ Then $\tan(\alpha+\beta)=\frac{\frac{3}{4}+\frac{5}{12}}{1-\frac{3}{4}\cdot\frac{5}{12}}=\frac{56}{33}$ Let $\theta$ be the smallest angle of the third triangle. Consider $\tan{90^\circ}=\tan((\alpha+\beta)+\theta)=\frac{\frac{56}{33}+\tan{\theta}}{1-\frac{56}{33}\cdot\tan{\theta}}$ In order for this to be undefined, we need $1-\frac{56}{33}\cdot\tan{\theta}=0$ so $\tan{\theta}=\frac{33}{56}$ Hence the base side lengths of the third triangle are $33$ and $56$ . By the Pythagorean Theorem, the hypotenuse of the third triangle is $65$ , so the perimeter is $33+56+65=\boxed{\textbf{(C) }154}$ .

~kafuu_chino

Solution 2 (Complex Number)

The smallest angle of $3-4-5$ triangle can be viewed as the arguement of $4+3i$ , and the smallest angle of $5-12-13$ triangle can be viewed as the arguement of $12+5i$ .

Hence, if we assume the ratio of the two shortest length of the last triangle is $1:k$ ( $k$ being some rational number), then we can derive the following formula of the sum of their arguement. Since their arguement adds up to $\frac{\pi}{2}$ , it's the arguement of $i$ . Hence, $\left(4+3i\right)\left(5+12i\right)\left(k+i\right)=ni\,,$ where $n$ is some real number.

Solving the equation, we get $56k-33=0\,,\quad 33k+56=n\,.$ Hence $k=\frac{33}{56}$

Since the sidelength of the theird triangle are co-prime integers, two of its sides are $33$ and $56$ . And the last side is $\sqrt{33^2+56^2}=65$ , hence, the parameter of the third triangle if $33+56+65=\boxed{\mathbf{(C)}\,154}$ .

~Prof. Joker

Solution 3 (Another Trig)

Denote the smallest angle of the $3-4-5$ triangle as $\alpha$ , the smallest angle of the $5-12-13$ triangle as $\beta$ , and the smallest angle of the triangle we are trying to solve for as $\theta$ . We then have $\alpha + \beta + \theta = 90$ $\alpha + \beta = 90 - \theta$ $\sin{(\alpha + \beta)} = \sin{(90 - \theta)} = \cos{\theta}$ $\cos{\theta} = \sin{\alpha}\cos{\beta} + \cos{\alpha}\sin{\beta} = (\frac{3}{5})(\frac{12}{13}) + (\frac{4}{5})(\frac{5}{13}) = \frac{56}{65}$ Taking the hypotenuse to be $65$ and one of the legs to be $56$ , we compute the last leg to be $\sqrt{65^2 - 56^2} = \sqrt{(65-56)(65+56)} = \sqrt{9*121} = 3*11 = 33$

Giving us a final answer of $65 + 56 + 33 = \boxed{\textbf{(C) }154}$ .

~tkl

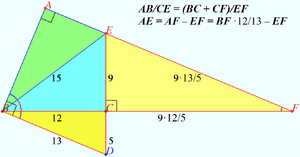
Solution 4 (Similarity)

Let's arrange the triangles $BCD (5-12-13), BCE (9-12-15)$ and $ABE$ as shown in the diagram. $F = AE \cap BC.$ $AE \perp AB, DB \perp AB \implies \triangle BCD \sim \triangle FCE \sim \triangle FAB \implies$ $EF = \frac{9 \cdot 13}{5}, CF = \frac{9 \cdot 12}{5}, BF = BC + CF = \frac{12 \cdot 14}{5},$ $\frac {AB}{CE} = \frac {BF}{EF} \implies AB = \frac{12 \cdot 14}{13},$ $AE = AF - EF = BF \cdot \frac {12}{13} - EF = \frac {99}{13} \implies$ $AE : AB : BE = 99 : 12 \cdot 14 : 15 \cdot 13 = 33 : 56 : 65 \implies 65 + 56 + 33 = \boxed{\textbf{(C) }154}$ vladimir.shelomovskii@gmail.com, vvsss

Solution 5 (Complex)

Suppose the triangle has legs $a, b$ . We want $\arctan \frac{3}{4} + \arctan\frac{5}{12} + \arctan\frac{a}{b} = \frac{\pi}{2}.$ This is equivalent to \begin{align*}

   \arg{e^{i\arctan\frac{3}{4}}\cdot e^{i\arctan\frac{5}{12}}\cdot e^{i\arctan\frac{a}{b}}} &= \frac{\pi}{2}\\
   \arg(4+3i)(12+5i)(b+ai) &= \frac{\pi}{2}\\  
  \arg\left( (33b -56a)+(33a + 56b)i\right) &= \frac{\pi}{2}

\end{align*} Since the argument of this complex number is $\frac{\pi}{2},$ its real part must be $0$ . Matching real and imaginary parts yields $33b = 56a,$ or $b = \frac{56}{33}a$ . The smallest pair $(a, b)$ that works is $(33, 56),$ which yields a hypotenuse of $65.$ The perimeter of this triangle is $33 + 56 + 65 = \boxed{\textbf{(C)\ 154}}.$

-Benedict T (countmath1)

Video Solution by Innovative Minds

https://youtu.be/9PMdtwkKTlU

Video Solution by SpreadTheMathLove

https://www.youtube.com/watch?v=cyiF8_5fEsM

@@ Line 53: / Line 53: @@
 <cmath>AE : AB : BE = 99 : 12 \cdot 14 : 15 \cdot 13 = 33 : 56 : 65 \implies 65 + 56 + 33 = \boxed{\textbf{(C) }154}</cmath>
 '''vladimir.shelomovskii@gmail.com, vvsss'''
+==Solution 5 (Complex)==
+Suppose the triangle has legs <math>a, b</math>. We want
+<cmath>\arctan \frac{3}{4} + \arctan\frac{5}{12} + \arctan\frac{a}{b} = \frac{\pi}{2}.</cmath>
+This is equivalent to
+\begin{align*}
+    \arg{e^{i\arctan\frac{3}{4}}\cdot e^{i\arctan\frac{5}{12}}\cdot e^{i\arctan\frac{a}{b}}} &= \frac{\pi}{2}\\
+    \arg(4+3i)(12+5i)(b+ai) &= \frac{\pi}{2}\\
+   \arg\left( (33b -56a)+(33a + 56b)i\right) &= \frac{\pi}{2}
+\end{align*}
+Since the argument of this complex number is <math>\frac{\pi}{2},</math> its real part must be <math>0</math>. Matching real and imaginary parts yields <math>33b = 56a,</math> or <math>b = \frac{56}{33}a</math>. The smallest pair <math>(a, b)</math> that works is <math>(33, 56),</math> which yields a hypotenuse of <math>65.</math> The perimeter of this triangle is <math>33 + 56 + 65 = \boxed{\textbf{(C)\ 154}}.</math>
+-Benedict T (countmath1)
 ==Video Solution by Innovative Minds==

2024 AMC 12B (Problems • Answer Key • Resources)
Preceded by Problem 20	Followed by Problem 22
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

Page

Toolbox

Search