Difference between revisions of "Bibhorr Formula"
(→Explanation) |
(→Explanation) |
||
| Line 11: | Line 11: | ||
==Explanation== | ==Explanation== | ||
[[File:Bibhorrformula.jpg]] | [[File:Bibhorrformula.jpg]] | ||
| + | |||
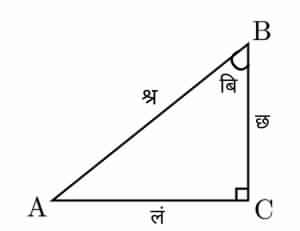
Consider a [[right triangle]] ABC, such that BC and AC are shortest and medium sides respectively and AB is the longest side or hypotenuse. Now, the angle opposite AC, called Bibhorr angle is given as: | Consider a [[right triangle]] ABC, such that BC and AC are shortest and medium sides respectively and AB is the longest side or hypotenuse. Now, the angle opposite AC, called Bibhorr angle is given as: | ||
| + | |||
[[File:download.png|250px]] | [[File:download.png|250px]] | ||
==See also== | ==See also== | ||
[[Trigonometry]] | [[Trigonometry]] | ||
Revision as of 10:14, 7 August 2018
Contents
Statement
For a given right triangle with longest side श्र, medium side लं and shortest side छ, the angle opposite the medium side (Bibhorr angle) बि is given as:
This equation is known as Bibhorr formula. The symbolical notations use Hindi letters and specifically denote the sides.
Units
The use of two constants - 90º or π/2 and 1.5 makes the formula more legible. These constants are known as "Bibhorr sthiron" and "Bibhorr constant" respectively.
Explanation
Consider a right triangle ABC, such that BC and AC are shortest and medium sides respectively and AB is the longest side or hypotenuse. Now, the angle opposite AC, called Bibhorr angle is given as: