Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2006 AMC 10B Problems/Problem 6"

m (added category)
m
Line 7: Line 7:
  
 
== Solution ==
 
== Solution ==
−
Since the side of the [[square]] is the [[diameter]] of the [[semicircle]], the [[radius]] of the semicircle is <math> \frac{1}{2}\cdot\frac{2}{\pi}=\frac{1}{\pi} </math>.
+
Since the side of the [[square (geometry) | square]] is the [[diameter]] of the [[semicircle]], the [[radius]] of the semicircle is <math> \frac{1}{2}\cdot\frac{2}{\pi}=\frac{1}{\pi} </math>.
  
 
Since the length of one of the semicircular [[arc]]s is half the [[circumference]] of the corresponding [[circle]], the length of one arc is <math> \frac{1}{2}\cdot2\cdot\pi\cdot\frac{1}{\pi}=1</math>.  
 
Since the length of one of the semicircular [[arc]]s is half the [[circumference]] of the corresponding [[circle]], the length of one arc is <math> \frac{1}{2}\cdot2\cdot\pi\cdot\frac{1}{\pi}=1</math>.  
  
−
Since the desired [[perimeter]] is made up of four of these arcs, the perimeter is <math>4\cdot1=4\Rightarrow D</math>
+
Since the desired [[perimeter]] is made up of four of these arcs, the perimeter is <math>4\cdot1=4\Rightarrow \mathrm{(D)}</math>
  
  

Revision as of 16:47, 17 October 2006

Problem

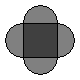
A region is bounded by semicircular arcs constructed on the side of a square whose sides measure $\frac{2}{\pi}$, as shown. What is the perimeter of this region?

2006amc10b06.gif

$\mathrm{(A) \ } \frac{4}{\pi}\qquad \mathrm{(B) \ } 2\qquad \mathrm{(C) \ } \frac{8}{\pi}\qquad \mathrm{(D) \ } 4\qquad \mathrm{(E) \ } \frac{16}{\pi}$

Solution

Since the side of the square is the diameter of the semicircle, the radius of the semicircle is $\frac{1}{2}\cdot\frac{2}{\pi}=\frac{1}{\pi}$.

Since the length of one of the semicircular arcs is half the circumference of the corresponding circle, the length of one arc is $\frac{1}{2}\cdot2\cdot\pi\cdot\frac{1}{\pi}=1$.

Since the desired perimeter is made up of four of these arcs, the perimeter is $4\cdot1=4\Rightarrow \mathrm{(D)}$


See Also

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2006_AMC_10B_Problems/Problem_6&oldid=10378"