Difference between revisions of "1985 AIME Problems/Problem 4"
(Solution) |
|||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
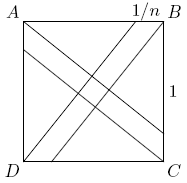
A small [[square (geometry) | square]] is constructed inside a square of [[area]] 1 by dividing each side of the unit square into <math>n</math> equal parts, and then connecting the [[vertex | vertices]] to the division points closest to the opposite vertices. Find the value of <math>n</math> if the the [[area]] of the small square is exactly <math>\frac1{1985}</math>. | A small [[square (geometry) | square]] is constructed inside a square of [[area]] 1 by dividing each side of the unit square into <math>n</math> equal parts, and then connecting the [[vertex | vertices]] to the division points closest to the opposite vertices. Find the value of <math>n</math> if the the [[area]] of the small square is exactly <math>\frac1{1985}</math>. | ||
| − | + | [[Image:AIME_1985_Problem_4.png]] | |
== Solution == | == Solution == | ||
The lines passing through <math>A</math> and <math>C</math> divide the square into three parts, two [[right triangle]]s and a [[parallelogram]]. The area of the [[triangle]]s together is easily seen to be <math>\frac{n - 1}{n}</math>, so the area of the parallelogram is <math>A = \frac{1}{n}</math>. By the [[Pythagorean Theorem]], the base of the parallelogram has [[length]] <math>l = \sqrt{1^2 + \left(\frac{n - 1}{n}\right)^2} = \frac{1}{n}\sqrt{2n^2 - 2n + 1}</math>, so the parallelogram has height <math>h = \frac{A}{l} = \frac{1}{\sqrt{2n^2 - 2n + 1}}</math>. But the height of the parallelogram is the side of the little square, so <math>2n^2 - 2n + 1 = 1985</math>. Solving this [[quadratic equation]] gives <math>n = 032</math>. | The lines passing through <math>A</math> and <math>C</math> divide the square into three parts, two [[right triangle]]s and a [[parallelogram]]. The area of the [[triangle]]s together is easily seen to be <math>\frac{n - 1}{n}</math>, so the area of the parallelogram is <math>A = \frac{1}{n}</math>. By the [[Pythagorean Theorem]], the base of the parallelogram has [[length]] <math>l = \sqrt{1^2 + \left(\frac{n - 1}{n}\right)^2} = \frac{1}{n}\sqrt{2n^2 - 2n + 1}</math>, so the parallelogram has height <math>h = \frac{A}{l} = \frac{1}{\sqrt{2n^2 - 2n + 1}}</math>. But the height of the parallelogram is the side of the little square, so <math>2n^2 - 2n + 1 = 1985</math>. Solving this [[quadratic equation]] gives <math>n = 032</math>. | ||
Revision as of 01:11, 21 January 2007
Problem
A small square is constructed inside a square of area 1 by dividing each side of the unit square into ![]() equal parts, and then connecting the vertices to the division points closest to the opposite vertices. Find the value of
equal parts, and then connecting the vertices to the division points closest to the opposite vertices. Find the value of ![]() if the the area of the small square is exactly
if the the area of the small square is exactly ![]() .
.
Solution
The lines passing through ![]() and
and ![]() divide the square into three parts, two right triangles and a parallelogram. The area of the triangles together is easily seen to be
divide the square into three parts, two right triangles and a parallelogram. The area of the triangles together is easily seen to be ![]() , so the area of the parallelogram is
, so the area of the parallelogram is ![]() . By the Pythagorean Theorem, the base of the parallelogram has length
. By the Pythagorean Theorem, the base of the parallelogram has length  , so the parallelogram has height
, so the parallelogram has height ![]() . But the height of the parallelogram is the side of the little square, so
. But the height of the parallelogram is the side of the little square, so ![]() . Solving this quadratic equation gives
. Solving this quadratic equation gives ![]() .
.









