Difference between revisions of "2021 USAJMO Problems/Problem 2"
m |
m (→See Also) |
||
| Line 22: | Line 22: | ||
{{USAJMO newbox|year=2021|num-b=1|num-a=3}} | {{USAJMO newbox|year=2021|num-b=1|num-a=3}} | ||
| − | [[Category:Olympiad | + | [[Category:Olympiad Geometry Problems]] |
{{MAA Notice}} | {{MAA Notice}} | ||
Revision as of 12:18, 16 April 2021
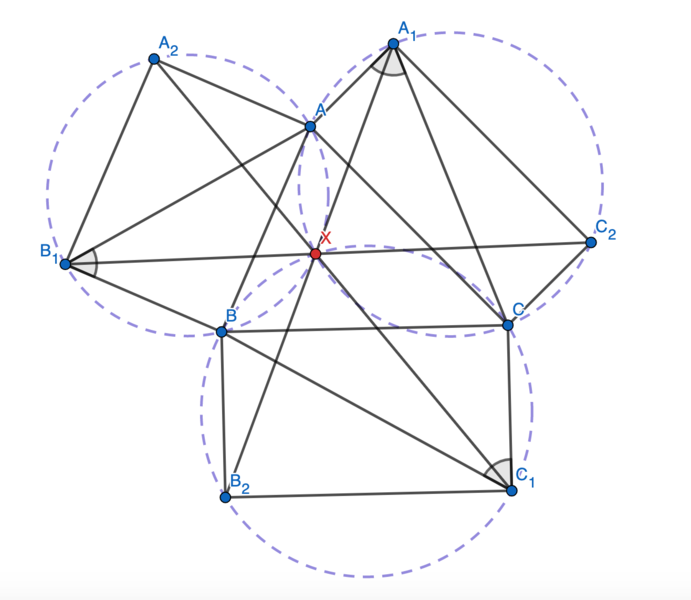
Problem
Rectangles ![]()
![]() and
and ![]() are erected outside an acute triangle
are erected outside an acute triangle ![]() Suppose that
Suppose that![]() Prove that lines
Prove that lines ![]()
![]() and
and ![]() are concurrent.
are concurrent.
Solution
We first claim that the three circles ![]()
![]() and
and ![]() are share a common intersection.
are share a common intersection.
Let the second intersection of ![]() and
and ![]() be
be ![]() . Then
. Then
 which implies that
which implies that ![]() is cyclic as desired.
is cyclic as desired.
Now we show that ![]() is the intersection of
is the intersection of ![]()
![]() and
and ![]() Note that
Note that ![]() so
so ![]() are collinear. Similarly,
are collinear. Similarly, ![]() and
and ![]() are collinear, so the three lines concur and we are done.
are collinear, so the three lines concur and we are done.
~Leonard_my_dude
See Also
| 2021 USAJMO (Problems • Resources) | ||
| Preceded by Problem 1 |
Followed by Problem 3 | |
| 1 • 2 • 3 • 4 • 5 • 6 | ||
| All USAJMO Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()