Difference between revisions of "1998 AIME Problems/Problem 9"
(problem/solution) |
|||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
| + | Two mathematicians take a morning coffee break each day. They arrive at the cafeteria independently, at random times between 9 a.m. and 10 a.m., and stay for exactly <math>m</math> mintues. The probability that either one arrives while the other is in the cafeteria is <math>40 \%,</math> and <math>m = a - b\sqrt {c},</math> where <math>a, b,</math> and <math>c</math> are positive integers, and <math>c</math> is not divisible by the square of any prime. Find <math>\displaystyle a + b + c.</math> | ||
| + | |||
| + | __TOC__ | ||
== Solution == | == Solution == | ||
| + | === Solution 1 === | ||
| + | Let the two mathematicians be <math>M_1</math> and <math>M_2</math>. Consider plotting the times that they are on break on a coordinate plane and shading in the places where they would be there at the same time as such. | ||
| + | |||
| + | We can count the area that we don't want in terms of <math>m</math> and solve: | ||
| + | <div style="text-align:center;"> | ||
| + | <math>\frac{(60-m)^2}{60^2} = .6</math> | ||
| + | <math>(60-m)^2 = 36\cdot 60</math> | ||
| + | <math>60 - m = 12\sqrt{15}</math> | ||
| + | <math>\Rightarrow m = 60-12\sqrt{15}</math> | ||
| + | </div> | ||
| + | So the answer is <math>60 + 12 + 15 = 087</math>. | ||
| + | |||
| + | === Solution 2 === | ||
| + | [[Image:AIME_1998-9.png|350px]] | ||
| + | |||
| + | [[Image:AIME_1998-9b.png|350px]] | ||
| + | |||
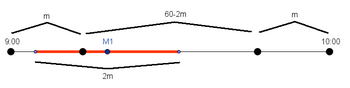
| + | We draw a number line representing the time interval. If mathematicion <math>M_1</math> comes in at the center of the time period, then the two mathematicions will meet if <math>M_2</math> comes in somewhere between <math>m</math> minutes before and after <math>M_1</math> comes (a total range of <math>2m</math> minutes). However, if <math>M_1</math> comes into the cafeteria in the first or last <math>m</math> minutes, then the range in which <math>M_2</math> is reduced to somewhere in between <math>m</math> and <math>2m</math>. | ||
| + | |||
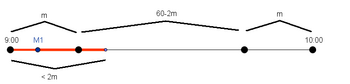
| + | We know try to find the weighted average of the chance that the two meet. In the central <math>\displaystyle 60-2m</math> minutes, <math>M_1</math> and <math>M_2</math> have to enter the cafeteria within <math>m</math> minutes of each other; so if we fix point <math>M_1</math> then <math>M_2</math> has a <math>\frac{2m}{60} = \frac{m}{30}</math> probability of meeting. | ||
| + | |||
| + | In the first and last <math>2m</math> minutes, the probability that the two meet ranges from <math>\frac{m}{60}</math> to <math>\frac{2m}{60}</math>, depending upon the location of <math>M_1</math> with respect to the endpoints. Intuitively, the average probability will occur at <math>\frac{\frac{3}{2}m}{60} = \frac{m}{40}</math>. | ||
| + | |||
| + | So the weighted average is: | ||
| + | :<math>\frac{\frac{m}{30}(60-2m) + \frac{m}{40}(2m)}{60} = \frac{40}{100}</math> | ||
| + | :<math>0 = \frac{m^2}{60} - 2m + \frac{2}{5}</math> | ||
| + | :<math>0 = m^2 - 120m + 1440</math> | ||
| + | |||
| + | Solving this [[quadratic equation|quadratic]], we get two roots, <math>\displaystyle 60 \pm 12\sqrt{15}</math>. However, <math>m < 60</math>, so we discard the greater root; and thus our answer <math>60 + 12 + 15 = 087</math>. | ||
== See also == | == See also == | ||
| − | + | {{AIME box|year=1998|num-b=8|num-a=10}} | |
| + | |||
| + | [[Category:Intermediate Combinatorics Problems]] | ||
Revision as of 10:07, 8 September 2007
Problem
Two mathematicians take a morning coffee break each day. They arrive at the cafeteria independently, at random times between 9 a.m. and 10 a.m., and stay for exactly 
mintues. The probability that either one arrives while the other is in the cafeteria is 
and 
where 
and 
are positive integers, and is not divisible by the square of any prime. Find 
Solution
Solution 1
Let the two mathematicians be 
and 
. Consider plotting the times that they are on break on a coordinate plane and shading in the places where they would be there at the same time as such.
We can count the area that we don't want in terms of and solve:
So the answer is 
.
Solution 2
We draw a number line representing the time interval. If mathematicion comes in at the center of the time period, then the two mathematicions will meet if comes in somewhere between minutes before and after comes (a total range of 
minutes). However, if comes into the cafeteria in the first or last minutes, then the range in which is reduced to somewhere in between and .
We know try to find the weighted average of the chance that the two meet. In the central 
minutes, and have to enter the cafeteria within minutes of each other; so if we fix point then has a 
probability of meeting.
In the first and last minutes, the probability that the two meet ranges from 
to 
, depending upon the location of with respect to the endpoints. Intuitively, the average probability will occur at 
.
So the weighted average is:
Solving this quadratic, we get two roots, 
. However, 
, so we discard the greater root; and thus our answer .
See also
| 1998 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 8 |
Followed by Problem 10 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
