Difference between revisions of "1987 AIME Problems/Problem 15"
(→Solution) |
|||
| Line 23: | Line 23: | ||
we get <math>\boxed{462}</math>. | we get <math>\boxed{462}</math>. | ||
| + | == Solution 4 (Algebra) == | ||
| + | <asy> | ||
| + | size(200); | ||
| + | pair A, B, C, D, E, F; | ||
| + | A = (0, 5); | ||
| + | B = (12, 0); | ||
| + | C = (0, 0); | ||
| + | D = (0, 60/17); | ||
| + | E = (60/17, 60/17); | ||
| + | F = (60/17, 0); | ||
| + | draw(A--B--C--cycle); | ||
| + | draw(D--E--F); | ||
| + | label("$A$",A,N); | ||
| + | label("$B$",B,dir(0)); | ||
| + | label("$C$",C,SW); | ||
| + | label("$D$",D,W); | ||
| + | label("$E$",E,NE); | ||
| + | label("$F$",F,S); | ||
| + | label("$S_1$",(30/17,30/17)); | ||
| + | </asy> | ||
| + | |||
| + | <asy> | ||
| + | size(200); | ||
| + | pair A, B, C, W, X, Y, Z; | ||
| + | A = (0, 5); | ||
| + | B = (12, 0); | ||
| + | C = (0, 0); | ||
| + | real m = 1.31004366812; | ||
| + | real n = 3.1441048035; | ||
| + | W = (0,m); | ||
| + | X = (m,m+n); | ||
| + | Y = (m+n,n); | ||
| + | Z = (n,0); | ||
| + | draw(A--B--C--cycle); | ||
| + | draw(W--X--Y--Z--cycle); | ||
| + | label("$A$",A,N); | ||
| + | label("$B$",B,dir(0)); | ||
| + | label("$C$",C,SW); | ||
| + | label("$W$",W,dir(180)); | ||
| + | label("$X$",X,NE); | ||
| + | label("$Y$",Y,NE); | ||
| + | label("$Z$",Z,S); | ||
| + | label("$S_2$",(2.22707423581,2.22707423581)); | ||
| + | </asy> | ||
| + | |||
| + | Label points as above. Let <math>x=AC</math>, <math>y=BC</math>, <math>s_1 = 21</math> be the side length of <math>S_1</math>, and <math>s_2 = \sqrt{440}</math> be the side length of <math>S_2</math>. | ||
| + | |||
| + | Since <math>\triangle ABC\sim\triangle AED</math>, we have <math>\frac{x}{y} = \frac{x-s_1}{s_1}</math> | ||
| + | |||
| + | <math>\implies xs_1=xy-ys_1</math> | ||
| + | |||
| + | <math>\implies xy=s_1(x+y)</math> | ||
| + | |||
| + | <math>\implies xy=21(x+y) \qquad \qquad (*)</math>. | ||
| + | |||
| + | Since <math>\triangle ABC\sim\triangle AWX\sim\triangle ZBY</math>, we have <math>s_2 + \frac{s_2x}{y} + \frac{s_2y}{x}=\sqrt{x^2+y^2}</math> | ||
| + | |||
| + | <math>\implies s_2(x^2+xy+y^2)=xy\sqrt{x^2+y^2}</math> | ||
| + | |||
| + | <math>\implies s_2^2(x^2+xy+y^2)^2 = x^2y^2(x^2+y^2)</math> | ||
| + | |||
| + | <math>\implies 440(x^2+xy+y^2)^2 = x^2y^2(x^2+y^2)</math> | ||
| + | |||
| + | Let <math>t=x+y</math>. Repeatedly applying <math>(*)</math>, we get | ||
| + | <cmath>440(t^2-21t)^2 = 441t^2(t^2 - 42t)</cmath> | ||
| + | <cmath>440(t-21)^2 = 441(t^2-42t)</cmath> | ||
| + | <cmath>440t^2 - 42\cdot 440t + 440\cdot 441 = 441t^2 - 441\cdot 42t</cmath> | ||
| + | <cmath>t^2-42t-440\cdot 441=0</cmath> | ||
| + | <cmath>(t-21)^2 = 441^2</cmath> | ||
| + | <cmath>t-21=441</cmath> | ||
| + | <cmath>t=\boxed{462}</cmath> | ||
| + | |||
| + | ~rayfish | ||
== See also == | == See also == | ||
{{AIME box|year=1987|num-b=14|after=Last<br />Question}} | {{AIME box|year=1987|num-b=14|after=Last<br />Question}} | ||
Revision as of 00:45, 27 December 2021
Contents
[hide]Problem
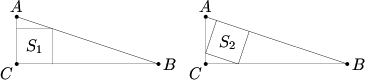
Squares ![]() and
and ![]() are inscribed in right triangle
are inscribed in right triangle ![]() , as shown in the figures below. Find
, as shown in the figures below. Find ![]() if area
if area ![]() and area
and area ![]() .
.
Solution
Because all the triangles in the figure are similar to triangle ![]() , it's a good idea to use area ratios. In the diagram above,
, it's a good idea to use area ratios. In the diagram above, ![]() Hence,
Hence, ![]() and
and ![]() . Additionally, the area of triangle
. Additionally, the area of triangle ![]() is equal to both
is equal to both ![]() and
and ![]()
Setting the equations equal and solving for ![]() ,
, ![]() . Therefore,
. Therefore, ![]() . However,
. However, ![]() is equal to the area of triangle
is equal to the area of triangle ![]() ! This means that the ratio between the areas
! This means that the ratio between the areas ![]() and
and ![]() is
is ![]() , and the ratio between the sides is
, and the ratio between the sides is ![]() . As a result,
. As a result, ![]() . We now need
. We now need ![]() to find the value of
to find the value of ![]() , because
, because ![]() .
.
Let ![]() denote the height to the hypotenuse of triangle
denote the height to the hypotenuse of triangle ![]() . Notice that
. Notice that ![]() . (The height of
. (The height of ![]() decreased by the corresponding height of
decreased by the corresponding height of ![]() ) Thus,
) Thus, ![]() . Because
. Because ![]() ,
, ![]() .
.
Easy Trig Solution
Let ![]() . Now using the 1st square,
. Now using the 1st square, ![]() and
and ![]() . Using the second square,
. Using the second square, ![]() . We have
. We have ![]() , or
, or ![]() Rearranging and letting
Rearranging and letting ![]() gives us
gives us ![]() We take the positive root, so
We take the positive root, so ![]() , which means
, which means ![]() .
.
Messy Trig Solution
Let ![]() be the smaller angle in the triangle. Then the sum of shorter and longer leg is
be the smaller angle in the triangle. Then the sum of shorter and longer leg is ![]() . We observe that the short leg has length
. We observe that the short leg has length ![]() . Grouping and squaring, we get
. Grouping and squaring, we get ![]() . Squaring and using the double angle identity for sine, we get,
. Squaring and using the double angle identity for sine, we get, ![]() . Solving, we get
. Solving, we get ![]() . Now to find
. Now to find ![]() , we find
, we find ![]() using the Pythagorean
Identity, and then use the tangent double angle identity. Thus,
using the Pythagorean
Identity, and then use the tangent double angle identity. Thus, ![]() . Substituting into the original sum,
we get
. Substituting into the original sum,
we get ![]() .
.
Solution 4 (Algebra)
![[asy] size(200); pair A, B, C, D, E, F; A = (0, 5); B = (12, 0); C = (0, 0); D = (0, 60/17); E = (60/17, 60/17); F = (60/17, 0); draw(A--B--C--cycle); draw(D--E--F); label("$A$",A,N); label("$B$",B,dir(0)); label("$C$",C,SW); label("$D$",D,W); label("$E$",E,NE); label("$F$",F,S); label("$S_1$",(30/17,30/17)); [/asy]](http://latex.artofproblemsolving.com/4/4/2/4429300bb60a1a8d2dc0d905616f7d3a18f3cf58.png)
![[asy] size(200); pair A, B, C, W, X, Y, Z; A = (0, 5); B = (12, 0); C = (0, 0); real m = 1.31004366812; real n = 3.1441048035; W = (0,m); X = (m,m+n); Y = (m+n,n); Z = (n,0); draw(A--B--C--cycle); draw(W--X--Y--Z--cycle); label("$A$",A,N); label("$B$",B,dir(0)); label("$C$",C,SW); label("$W$",W,dir(180)); label("$X$",X,NE); label("$Y$",Y,NE); label("$Z$",Z,S); label("$S_2$",(2.22707423581,2.22707423581)); [/asy]](http://latex.artofproblemsolving.com/b/b/b/bbb3f5cd62d761e088f4f0d1c88b7e71d3e0a651.png)
Label points as above. Let ![]() ,
, ![]() ,
, ![]() be the side length of
be the side length of ![]() , and
, and ![]() be the side length of
be the side length of ![]() .
.
Since ![]() , we have
, we have ![]()
![]()
![]()
![]() .
.
Since ![]() , we have
, we have ![]()
![]()
![]()
![]()
Let ![]() . Repeatedly applying
. Repeatedly applying ![]() , we get
, we get
![]()
![]()
![]()
![]()
![]()
![]()
![]()
~rayfish
See also
| 1987 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Last Question | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()