Difference between revisions of "1989 AIME Problems/Problem 15"
(→Solution: added solution) |
m (→Solution 1: formatting) |
||
| Line 5: | Line 5: | ||
== Solutions == | == Solutions == | ||
| − | == Solution 1 == | + | === Solution 1 === |
Let <math>[RST]</math> be the area of polygon <math>RST</math>. We'll make use of the following fact: if <math>P</math> is a point in the interior of triangle <math>XYZ</math>, and line <math>XP</math> intersects line <math>YZ</math> at point <math>L</math>, then <math>\dfrac{XP}{PL} = \frac{[XPY] + [ZPX]}{[YPZ]}.</math> | Let <math>[RST]</math> be the area of polygon <math>RST</math>. We'll make use of the following fact: if <math>P</math> is a point in the interior of triangle <math>XYZ</math>, and line <math>XP</math> intersects line <math>YZ</math> at point <math>L</math>, then <math>\dfrac{XP}{PL} = \frac{[XPY] + [ZPX]}{[YPZ]}.</math> | ||
Revision as of 01:29, 10 April 2022
Contents
[hide]Problem
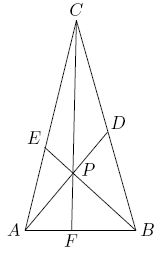
Point ![]() is inside
is inside ![]() . Line segments
. Line segments ![]() ,
, ![]() , and
, and ![]() are drawn with
are drawn with ![]() on
on ![]() ,
, ![]() on
on ![]() , and
, and ![]() on
on ![]() (see the figure below). Given that
(see the figure below). Given that ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , find the area of
, find the area of ![]() .
.
Solutions
Solution 1
Let ![]() be the area of polygon
be the area of polygon ![]() . We'll make use of the following fact: if
. We'll make use of the following fact: if ![]() is a point in the interior of triangle
is a point in the interior of triangle ![]() , and line
, and line ![]() intersects line
intersects line ![]() at point
at point ![]() , then
, then ![]()
![[asy] size(170); pair X = (1,2), Y = (0,0), Z = (3,0); real x = 0.4, y = 0.2, z = 1-x-y; pair P = x*X + y*Y + z*Z; pair L = y/(y+z)*Y + z/(y+z)*Z; draw(X--Y--Z--cycle); draw(X--P); draw(P--L, dotted); draw(Y--P--Z); label("$X$", X, N); label("$Y$", Y, S); label("$Z$", Z, S); label("$P$", P, NE); label("$L$", L, S);[/asy]](http://latex.artofproblemsolving.com/3/c/9/3c978a1fdb0a6c3a79b9ee477956a440b734f13b.png)
This is true because triangles ![]() and
and ![]() have their areas in ratio
have their areas in ratio ![]() (as they share a common height from
(as they share a common height from ![]() ), and the same is true of triangles
), and the same is true of triangles ![]() and
and ![]() .
.
We'll also use the related fact that ![]() . This is slightly more well known, as it is used in the standard proof of Ceva's theorem.
. This is slightly more well known, as it is used in the standard proof of Ceva's theorem.
Now we'll apply these results to the problem at hand.
![[asy] size(170); pair C = (1, 3), A = (0,0), B = (1.7,0); real a = 0.5, b= 0.25, c = 0.25; pair P = a*A + b*B + c*C; pair D = b/(b+c)*B + c/(b+c)*C; pair EE = c/(c+a)*C + a/(c+a)*A; pair F = a/(a+b)*A + b/(a+b)*B; draw(A--B--C--cycle); draw(A--P); draw(B--P--C); draw(P--D, dotted); draw(EE--P--F, dotted); label("$A$", A, S); label("$B$", B, S); label("$C$", C, N); label("$D$", D, NE); label("$E$", EE, NW); label("$F$", F, S); label("$P$", P, E); [/asy]](http://latex.artofproblemsolving.com/7/c/9/7c9e14d181ecf013675ff1bfbe1aee4cc51d0c7e.png)
Since ![]() , this means that
, this means that ![]() ; thus
; thus ![]() has half the area of
has half the area of ![]() . And since
. And since ![]() , we can conclude that
, we can conclude that ![]() has one third of the combined areas of triangle
has one third of the combined areas of triangle ![]() and
and ![]() , and thus
, and thus ![]() of the area of
of the area of ![]() . This means that
. This means that ![]() is left with
is left with ![]() of the area of triangle
of the area of triangle ![]() :
:
![]() Since
Since ![]() , and since
, and since ![]() , this means that
, this means that ![]() is the midpoint of
is the midpoint of ![]() .
.
Furthermore, we know that ![]() , so
, so ![]() .
.
We now apply Stewart's theorem to segment ![]() in
in ![]() —or rather, the simplified version for a median. This tells us that
—or rather, the simplified version for a median. This tells us that
![]() Plugging in we know, we learn that
Plugging in we know, we learn that
![]() Happily,
Happily, ![]() is also equal to 117. Therefore
is also equal to 117. Therefore ![]() is a right triangle with a right angle at
is a right triangle with a right angle at ![]() ; its area is thus
; its area is thus ![]() . As
. As ![]() is a median of
is a median of ![]() , the area of
, the area of ![]() is twice this, or 54. And we already know that
is twice this, or 54. And we already know that ![]() has half the area of
has half the area of ![]() , which must therefore be 108.
, which must therefore be 108.
Solution 2
Because we're given three concurrent cevians and their lengths, it seems very tempting to apply Mass points. We immediately see that ![]() ,
, ![]() , and
, and ![]() . Now, we recall that the masses on the three sides of the triangle must be balanced out, so
. Now, we recall that the masses on the three sides of the triangle must be balanced out, so ![]() and
and ![]() . Thus,
. Thus, ![]() and
and ![]() .
.
Recalling that ![]() , we see that
, we see that ![]() and
and ![]() is a median to
is a median to ![]() in
in ![]() . Applying Stewart's Theorem,
. Applying Stewart's Theorem, ![]() , and
, and ![]() . Now notice that
. Now notice that ![]() , because both triangles share the same base and the
, because both triangles share the same base and the ![]() . Applying Heron's formula on triangle
. Applying Heron's formula on triangle ![]() with sides
with sides ![]() ,
, ![]() , and
, and ![]() ,
, ![]() and
and ![]() .
.
Solution 3
Using a different form of Ceva's Theorem, we have ![]()
Solving ![]() and
and ![]() , we obtain
, we obtain ![]() and
and ![]() .
.
Let ![]() be the point on
be the point on ![]() such that
such that ![]() .
Since
.
Since ![]() and
and ![]() ,
, ![]() . (Stewart's Theorem)
. (Stewart's Theorem)
Also, since ![]() and
and ![]() , we see that
, we see that ![]() ,
, ![]() , etc. (Stewart's Theorem)
Similarly, we have
, etc. (Stewart's Theorem)
Similarly, we have ![]() (
(![]() ) and thus
) and thus ![]() .
.
![]() is a
is a ![]() right triangle, so
right triangle, so ![]() (
(![]() ) is
) is ![]() .
Therefore, the area of
.
Therefore, the area of ![]() .
Using area ratio,
.
Using area ratio, ![]() .
.
Solution 4
Because the length of cevian ![]() is unknown, we can examine what happens when we extend it or decrease its length and see that it simply changes the angles between the cevians. Wouldn't it be great if it the length of
is unknown, we can examine what happens when we extend it or decrease its length and see that it simply changes the angles between the cevians. Wouldn't it be great if it the length of ![]() was such that
was such that ![]() ? Let's first assume it's a right angle and hope that everything works out.
? Let's first assume it's a right angle and hope that everything works out.
Extend ![]() to
to ![]() so that
so that ![]() . The result is that
. The result is that ![]() ,
, ![]() , and
, and ![]() because
because ![]() . Now we see that if we are able to show that
. Now we see that if we are able to show that ![]() , that is
, that is ![]() , then our right angle assumption will be true.
, then our right angle assumption will be true.
Apply the Pythagorean Theorem on ![]() to get
to get ![]() , so
, so ![]() and
and ![]() . Now, we apply the Law of Cosines on triangles
. Now, we apply the Law of Cosines on triangles ![]() and
and ![]() .
.
Let ![]() . Notice that
. Notice that ![]() and
and ![]() , so we get two nice equations.
, so we get two nice equations.
![]()
![]()
Solving, ![]() (yay!).
(yay!).
Now, the area is easy to find. ![]() .
.
[however, I think this solution is wrong, the A, B, and Cs do not match with the picture]
Solution 5
First, let ![]() and
and ![]() Thus, we can easily find that
Thus, we can easily find that ![]() Now,
Now, ![]() In the same manner, we find that
In the same manner, we find that ![]() Now, we can find that
Now, we can find that ![]() We can now use this to find that
We can now use this to find that ![]() Plugging this value in, we find that
Plugging this value in, we find that ![]() Now, since
Now, since ![]() we can find that
we can find that ![]() Setting
Setting ![]() we can apply Stewart's Theorem on triangle
we can apply Stewart's Theorem on triangle ![]() to find that
to find that ![]() Solving, we find that
Solving, we find that ![]() But,
But, ![]() meaning that
meaning that ![]() Since
Since ![]() we conclude that the answer is
we conclude that the answer is ![]() .
.
Solution 5(Mass of a point+ Stewart+heron)
Firstly, since they all meet at one single point, denoting the mass of them separately. Assuming ![]() ; we can get that
; we can get that ![]() ; which leads to the ratio between segments,
; which leads to the ratio between segments,
![]() . Denoting that
. Denoting that ![]()
Now we know three cevians' length, Applying Stewart theorem to them, getting three different equations:

After solving the system of equation, we get that ![]() ;
;
pulling ![]() back to get the length of
back to get the length of ![]() ; now we can apply Heron's formula here, which is
; now we can apply Heron's formula here, which is 
Our answer is ![]() ~bluesoul
~bluesoul
See also
| 1989 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Final Question | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.