Difference between revisions of "2021 IMO Problems/Problem 3"
(→Solution) |
(→Solution) |
||
| Line 42: | Line 42: | ||
<math>\boldsymbol{Lemma \hspace{3mm}2}</math> | <math>\boldsymbol{Lemma \hspace{3mm}2}</math> | ||
| − | Let the point <math>Y</math> be the radical center of the circles <math>\omega, \omega', \omega_1.</math> It has the same | + | Let the point <math>Y</math> be the radical center of the circles <math>\omega, \omega', \omega_1.</math> It has the same power <math>\nu</math> with respect to these circles. |
The common chords of the pairs of circles <math>A'B, AC, DT</math> intersect at this point. | The common chords of the pairs of circles <math>A'B, AC, DT</math> intersect at this point. | ||
| − | <math>Y</math> has | + | <math>Y</math> has power <math>\nu</math> with respect to <math>\Omega_1</math> since <math>A'B</math> is the radical axis of <math>\omega', \omega_1, \Omega_1.</math> |
| − | <math>Y</math> has | + | <math>Y</math> has power <math>\nu</math> with respect to <math>\Omega_1</math> since <math>XE</math> containing <math>Y</math> is the radical axis of <math>\Omega</math> and <math>\Omega_1.</math> |
| − | Hence <math>Y</math> has | + | Hence <math>Y</math> has power <math>\nu</math> with respect to <math>\omega, \omega', \Omega.</math> |
| − | ''' | + | '''vladimir.shelomovskii@gmail.com, vvsss, www.deoma–cmd.ru''' |
==Video solution== | ==Video solution== | ||
https://youtu.be/cI9p-Z4-Sc8 [Video contains solutions to all day 1 problems] | https://youtu.be/cI9p-Z4-Sc8 [Video contains solutions to all day 1 problems] | ||
Revision as of 16:26, 22 July 2022
Problem
Let ![]() be an interior point of the acute triangle
be an interior point of the acute triangle ![]() with
with ![]() so that
so that ![]() . The point
. The point ![]() on the segment
on the segment ![]() satisfies
satisfies ![]() , the point
, the point ![]() on the segment
on the segment ![]() satisfies
satisfies ![]() , and the point
, and the point ![]() on the line
on the line ![]() satisfies
satisfies ![]() . Let
. Let ![]() and
and ![]() be the circumcentres of the triangles
be the circumcentres of the triangles ![]() and
and ![]() respectively. Prove that the lines
respectively. Prove that the lines ![]() ,
, ![]() , and
, and ![]() are concurrent.
are concurrent.
Solution
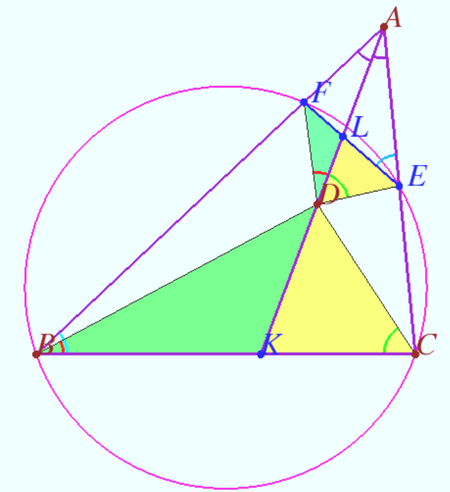
By statement point ![]() is located on the bisector
is located on the bisector ![]() of
of ![]() Let
Let ![]() be the intersection point of the tangent to the circle
be the intersection point of the tangent to the circle ![]() at the point
at the point ![]() and the line
and the line ![]() is inverse to
is inverse to ![]() with respect to the circle
with respect to the circle ![]() centered at
centered at ![]() with radius
with radius ![]() Then the pairs of points
Then the pairs of points ![]() and
and ![]() and
and ![]() are inverse with respect to
are inverse with respect to ![]() , so the points
, so the points ![]() and
and ![]() are collinear. Quadrilaterals containing the pairs of inverse points
are collinear. Quadrilaterals containing the pairs of inverse points ![]() and
and ![]() and
and ![]() and
and ![]() are inscribed,
are inscribed, ![]() is antiparallel to
is antiparallel to ![]() with respect to angle
with respect to angle ![]()
![]() .
.
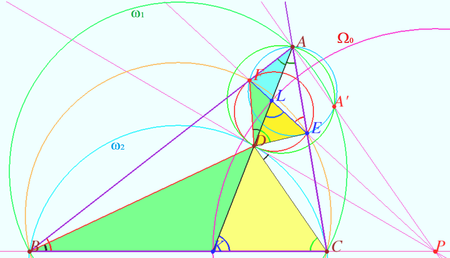
Consider the circles ![]() centered at
centered at ![]()
![]() centered at
centered at ![]() and
and ![]()
Denote ![]() . Then
. Then ![]()
![]() is cyclic),
is cyclic),
![]() is cyclic,
is cyclic, ![]() is antiparallel),
is antiparallel),
![]()
![]() is the point of the circle
is the point of the circle ![]()
Let Y be the radical center of the circles ![]() and
and ![]() Let
Let ![]() be the point of intersection
be the point of intersection ![]() let
let ![]() be the point of intersection
be the point of intersection ![]() Since the circles
Since the circles ![]() and
and ![]() are inverse with respect to
are inverse with respect to ![]() then
then ![]() lies on
lies on ![]() and
and ![]() lies on the perpendicular bisector of
lies on the perpendicular bisector of ![]() The power of a point
The power of a point ![]() with respect to the circles
with respect to the circles ![]() and
and ![]() are the same
are the same ![]() so
so ![]() the points
the points ![]() and
and ![]() coincide.
coincide.
The centers of the circles ![]() and
and ![]() (
(![]() and
and ![]() ) are located on the perpendicular bisector
) are located on the perpendicular bisector ![]() , the point
, the point ![]() is located on the perpendicular bisector
is located on the perpendicular bisector ![]() and, therefore, the points
and, therefore, the points ![]() and
and ![]() lie on a line, that is, the lines
lie on a line, that is, the lines ![]() and
and ![]() are concurrent.
are concurrent.
![]()
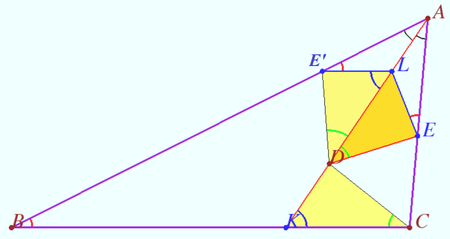
Let ![]() be bisector of the triangle
be bisector of the triangle ![]() , point
, point ![]() lies on
lies on ![]() The point
The point ![]() on the segment
on the segment ![]() satisfies
satisfies ![]() . The point
. The point ![]() is symmetric to
is symmetric to ![]() with respect to
with respect to ![]() The point
The point ![]() on the segment
on the segment ![]() satisfies
satisfies ![]() Then
Then ![]() and
and ![]() are antiparallel with respect to the sides of an angle
are antiparallel with respect to the sides of an angle ![]() and
and ![]() Proof
Proof
Symmetry of points ![]() and
and ![]() with respect bisector
with respect bisector ![]() implies
implies ![]()
![]()
![]()
![]()
![]() Corollary
Corollary
In the given problem ![]() and
and ![]() are antiparallel with respect to the sides of an angle
are antiparallel with respect to the sides of an angle ![]() quadrangle
quadrangle ![]() is concyclic.
is concyclic.
![]()
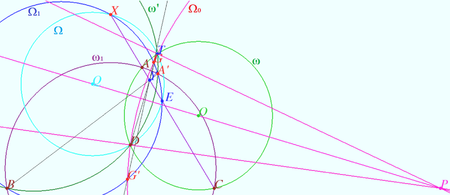
Let the point ![]() be the radical center of the circles
be the radical center of the circles ![]() It has the same power
It has the same power ![]() with respect to these circles.
The common chords of the pairs of circles
with respect to these circles.
The common chords of the pairs of circles ![]() intersect at this point.
intersect at this point.
![]() has power
has power ![]() with respect to
with respect to ![]() since
since ![]() is the radical axis of
is the radical axis of ![]()
![]() has power
has power ![]() with respect to
with respect to ![]() since
since ![]() containing
containing ![]() is the radical axis of
is the radical axis of ![]() and
and ![]()
Hence ![]() has power
has power ![]() with respect to
with respect to ![]()
vladimir.shelomovskii@gmail.com, vvsss, www.deoma–cmd.ru
Video solution
https://youtu.be/cI9p-Z4-Sc8 [Video contains solutions to all day 1 problems]