Difference between revisions of "2018 IMO Problems/Problem 6"
(→Solution) |
(→Solution) |
||
| Line 69: | Line 69: | ||
<cmath>\frac {BX}{DY} = \frac {R^2}{OD \cdot OY} ,\frac {DX}{BY} = \frac{R^2}{OB \cdot OY}.</cmath> | <cmath>\frac {BX}{DY} = \frac {R^2}{OD \cdot OY} ,\frac {DX}{BY} = \frac{R^2}{OB \cdot OY}.</cmath> | ||
<cmath>\frac{BX}{DX} =\frac{DY}{BY} \cdot \frac {OB}{OD} = \frac{AD}{BC} \cdot \frac{BC}{CD} \cdot \frac{AB}{AD} = \frac{AB}{CD}.</cmath> | <cmath>\frac{BX}{DX} =\frac{DY}{BY} \cdot \frac {OB}{OD} = \frac{AD}{BC} \cdot \frac{BC}{CD} \cdot \frac{AB}{AD} = \frac{AB}{CD}.</cmath> | ||
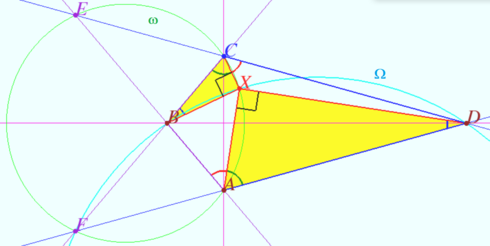
| − | [[File:2018 IMO 6 angles.png| | + | [[File:2018 IMO 6 angles.png|370px|right]] |
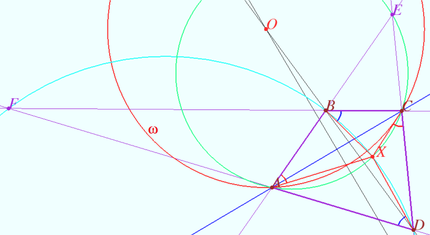
| + | [[File:2018 IMO 6 Claim 3.png|370px|right]] | ||
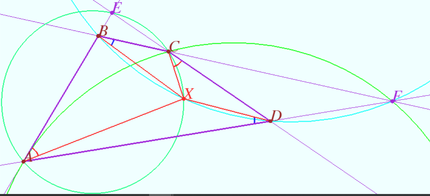
| + | [[File:2018 IMO 6a.png|430px|right]] | ||
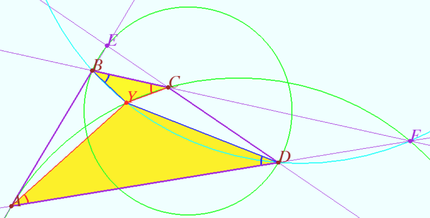
| + | [[File:2018 IMO 60.png|430px|right]] | ||
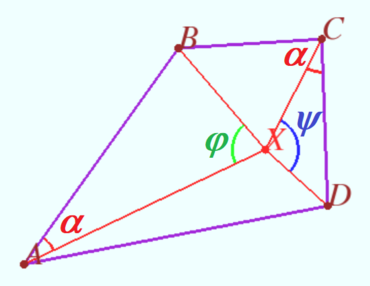
Denote <math>\angle XAB = \angle XCD = \alpha, \angle BXA = \varphi, \angle DXC = \psi.</math> | Denote <math>\angle XAB = \angle XCD = \alpha, \angle BXA = \varphi, \angle DXC = \psi.</math> | ||
| Line 85: | Line 88: | ||
<i><b>Claim 1</b></i> Let <math>A, C,</math> and <math>E</math> be arbitrary points on a circle <math>\omega, l</math> be the perpendicular bisector to the segment <math>AC.</math> Then the straight lines <math>AE</math> and <math>CE</math> intersect <math>l</math> at the points <math>B</math> and <math>D,</math> symmetric with respect to <math>\omega.</math> | <i><b>Claim 1</b></i> Let <math>A, C,</math> and <math>E</math> be arbitrary points on a circle <math>\omega, l</math> be the perpendicular bisector to the segment <math>AC.</math> Then the straight lines <math>AE</math> and <math>CE</math> intersect <math>l</math> at the points <math>B</math> and <math>D,</math> symmetric with respect to <math>\omega.</math> | ||
| − | + | ||
| − | |||
<i><b>Claim 2</b></i> Let points <math>B</math> and <math>D</math> be symmetric with respect to the circle <math>\omega.</math> Then any circle <math>\Omega</math> passing through these points is orthogonal to <math>\omega.</math> | <i><b>Claim 2</b></i> Let points <math>B</math> and <math>D</math> be symmetric with respect to the circle <math>\omega.</math> Then any circle <math>\Omega</math> passing through these points is orthogonal to <math>\omega.</math> | ||
| Line 102: | Line 104: | ||
Consequently, the angles <math>\angle AFC = \angle ADB – \angle FBD = \angle AGE - \angle CGE = \angle AGC.</math> | Consequently, the angles <math>\angle AFC = \angle ADB – \angle FBD = \angle AGE - \angle CGE = \angle AGC.</math> | ||
These angles subtend the <math>\overset{\Large\frown} {AC}</math> of the <math>ACF</math> circle, that is, the point <math>G,</math> symmetric to the point <math>E</math> with respect to <math>\omega,</math> belongs to the circle <math>ACF.</math> | These angles subtend the <math>\overset{\Large\frown} {AC}</math> of the <math>ACF</math> circle, that is, the point <math>G,</math> symmetric to the point <math>E</math> with respect to <math>\omega,</math> belongs to the circle <math>ACF.</math> | ||
| + | |||
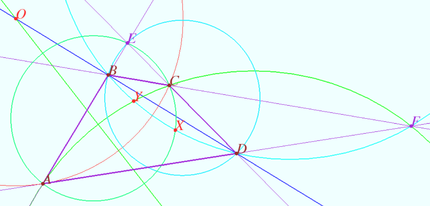
| + | <i><b>Attention</b></i> The uniqueness of the point <math>X</math> has not been proven. In the figure, the blue and green curves show the locus points with equal pairs of angles for one case. In the general case, one can divide the plane into parts and prove that the point <math>X</math> cannot be outside <math>ABCD.</math> It's not done here. | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
Revision as of 08:58, 22 August 2022
A convex quadrilateral ![]() satisfies
satisfies ![]() Point
Point ![]() lies inside
lies inside
![]() so that
so that
![]() and
and ![]() Prove that
Prove that ![]()
Solution
Suppose point X is unique. We will construct point ![]() and prove that
and prove that ![]() coincides with the point
coincides with the point ![]()
Special case
Let ![]() and
and ![]()
Let ![]() and
and ![]() be the intersection points of
be the intersection points of ![]() and
and ![]() and
and ![]() and
and ![]() respectively.
respectively.
The points ![]() and
and ![]() are symmetric with respect to the circle
are symmetric with respect to the circle ![]() (Claim 1).
(Claim 1).
The circle ![]() is orthogonal to the circle
is orthogonal to the circle ![]() (Claim 2).
(Claim 2).
Let ![]() be the point of intersection of the circles
be the point of intersection of the circles ![]() and
and ![]() Quadrilateral
Quadrilateral ![]() is cyclic
is cyclic ![]()
![]()
Similarly, quadrangle ![]() is cyclic
is cyclic ![]() . This means that point
. This means that point ![]() coincides with the point
coincides with the point ![]() .
.
![]() of
of ![]()
![]() of
of ![]()
The sum ![]() (Claim 3)
(Claim 3) ![]()
![]()
Similarly, ![]()
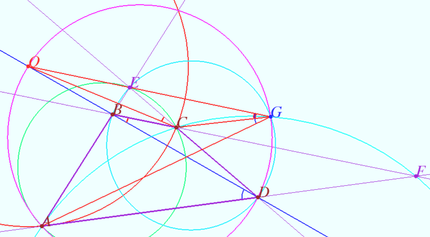
Common case
Denote by ![]() the intersection point of
the intersection point of ![]() and the perpendicular bisector of
and the perpendicular bisector of ![]() Let
Let ![]() be a circle (red) with center
be a circle (red) with center ![]() and radius
and radius ![]()
The points ![]() and
and ![]() are symmetric with respect to the circle
are symmetric with respect to the circle ![]() (Claim 1).
(Claim 1).
The circles ![]() and
and ![]() are orthogonal to the circle
are orthogonal to the circle ![]() (Claim 2).
(Claim 2).
Circles ![]() and
and ![]() are symmetric with respect to the circle
are symmetric with respect to the circle ![]() (Lemma).
(Lemma).
Denote by ![]() the point of intersection of the circles
the point of intersection of the circles ![]() and
and ![]() Quadrangle
Quadrangle ![]() is cyclic
is cyclic ![]() (see Special case).
Similarly, quadrangle
(see Special case).
Similarly, quadrangle ![]() is cyclic
is cyclic ![]()
This means that point ![]() coincides with the point
coincides with the point ![]() .
.
Denote by ![]() the point of intersection of circles
the point of intersection of circles ![]() and
and ![]()
Quadrangle ![]() is cyclic
is cyclic ![]()
Quadrangle ![]() is cyclic
is cyclic ![]()
The triangles ![]() by two angles, so
by two angles, so ![]()
The points ![]() and
and ![]() are symmetric with respect to the circle
are symmetric with respect to the circle ![]() , since they lie on the intersection of the circles
, since they lie on the intersection of the circles ![]() and
and ![]() symmetric with respect to
symmetric with respect to ![]() and the circle
and the circle ![]() orthogonal to
orthogonal to ![]()
The point ![]() is symmetric to itself, the point
is symmetric to itself, the point ![]() is symmetric to
is symmetric to ![]() with respect to
with respect to ![]() Usung
Usung ![]() and the equality
and the equality ![]() we get
we get ![]() The point
The point ![]() is symmetric to itself, the point
is symmetric to itself, the point ![]() is symmetric to
is symmetric to ![]() with respect to
with respect to ![]()
![]()
![]() The point
The point ![]() is symmetric to
is symmetric to ![]() and the point
and the point ![]() is symmetric to
is symmetric to ![]() with respect to
with respect to ![]() hence
hence
![]()
![]()
Denote ![]()
By the law of sines for ![]() we obtain
we obtain ![]()
By the law of sines for ![]() we obtain
we obtain ![]()
Hence we get ![]()
If ![]() then
then ![]()
![]() This is a special case.
This is a special case.
In all other cases, the equality of the sines follows ![]()
Claim 1 Let ![]() and
and ![]() be arbitrary points on a circle
be arbitrary points on a circle ![]() be the perpendicular bisector to the segment
be the perpendicular bisector to the segment ![]() Then the straight lines
Then the straight lines ![]() and
and ![]() intersect
intersect ![]() at the points
at the points ![]() and
and ![]() symmetric with respect to
symmetric with respect to ![]()
Claim 2 Let points ![]() and
and ![]() be symmetric with respect to the circle
be symmetric with respect to the circle ![]() Then any circle
Then any circle ![]() passing through these points is orthogonal to
passing through these points is orthogonal to ![]()
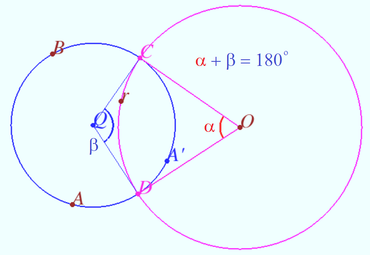
Claim 3 The sum of the arcs between the points of intersection of two perpendicular circles is ![]() In the figure they are a blue and red arcs
In the figure they are a blue and red arcs ![]()
Lemma The opposite sides of the quadrilateral ![]() intersect at points
intersect at points ![]() and
and ![]() (
(![]() lies on
lies on ![]() ). The circle
). The circle ![]() centered at the point
centered at the point ![]() contains the ends of the diagonal
contains the ends of the diagonal ![]() The points
The points ![]() and
and ![]() are symmetric with respect to the circle
are symmetric with respect to the circle ![]() (in other words, the inversion with respect to
(in other words, the inversion with respect to ![]() maps
maps ![]() into
into ![]() Then the circles
Then the circles ![]() and
and ![]() are symmetric with respect to
are symmetric with respect to ![]()
Proof We will prove that the point ![]() symmetric to the point
symmetric to the point ![]() with respect to
with respect to ![]() belongs to the circle
belongs to the circle ![]() For this, we will prove the equality
For this, we will prove the equality ![]()
A circle ![]() containing points
containing points ![]() and
and ![]() symmetric with respect to
symmetric with respect to ![]() is orthogonal to
is orthogonal to ![]() (Claim 2) and maps into itself under inversion with respect to the circle
(Claim 2) and maps into itself under inversion with respect to the circle ![]() Hence, the point
Hence, the point ![]() under this inversion passes to some point
under this inversion passes to some point ![]() of the same circle
of the same circle ![]()
A straight line ![]() containing the point
containing the point ![]() of the circle
of the circle ![]() under inversion with respect to
under inversion with respect to ![]() maps into the circle
maps into the circle ![]() Hence, the inscribed angles of this circle are equal
Hence, the inscribed angles of this circle are equal ![]()
![]() maps into
maps into ![]() and
and ![]() maps into
maps into ![]() Consequently, the angles
Consequently, the angles ![]() These angles subtend the
These angles subtend the ![]() of the
of the ![]() circle, that is, the point
circle, that is, the point ![]() symmetric to the point
symmetric to the point ![]() with respect to
with respect to ![]() belongs to the circle
belongs to the circle ![]()
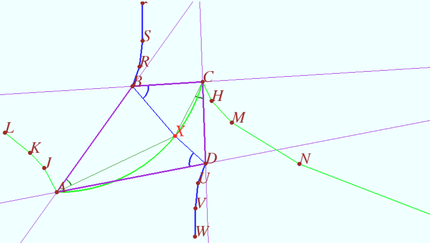
Attention The uniqueness of the point ![]() has not been proven. In the figure, the blue and green curves show the locus points with equal pairs of angles for one case. In the general case, one can divide the plane into parts and prove that the point
has not been proven. In the figure, the blue and green curves show the locus points with equal pairs of angles for one case. In the general case, one can divide the plane into parts and prove that the point ![]() cannot be outside
cannot be outside ![]() It's not done here.
It's not done here.
vladimir.shelomovskii@gmail.com, vvsss