Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1987 AIME Problems/Problem 15"

(solution by 4everwise, img needed)
(→‎Solution)
Line 10: Line 10:
 
Setting the equations equal and solving for <math>T_5</math>, <math>T_5 = 1 + T_1 - T_3 + T_2 - T_4 = 1 + \frac {T_1}{441} + \frac {T_2}{441}</math>. Therefore, <math>441T_5 = 441 + T_1 + T_2</math>. However, <math>441 + T_1 + T_2</math> is equal to the area of triangle <math>ABC</math>! This means that the ratio between the areas <math>T_5</math> and <math>ABC</math> is <math>441</math>, and the ratio between the sides is <math>\sqrt {441} = 21</math>. As a result, <math>AB = 21\sqrt {440} = \sqrt {AC^2 + BC^2}</math>. We now need <math>(AC)(BC)</math> to find the value of <math>AC + BC</math>, because <math>AB^2 + 2(AC)(BC) = (AC + BC)^2</math>.
 
Setting the equations equal and solving for <math>T_5</math>, <math>T_5 = 1 + T_1 - T_3 + T_2 - T_4 = 1 + \frac {T_1}{441} + \frac {T_2}{441}</math>. Therefore, <math>441T_5 = 441 + T_1 + T_2</math>. However, <math>441 + T_1 + T_2</math> is equal to the area of triangle <math>ABC</math>! This means that the ratio between the areas <math>T_5</math> and <math>ABC</math> is <math>441</math>, and the ratio between the sides is <math>\sqrt {441} = 21</math>. As a result, <math>AB = 21\sqrt {440} = \sqrt {AC^2 + BC^2}</math>. We now need <math>(AC)(BC)</math> to find the value of <math>AC + BC</math>, because <math>AB^2 + 2(AC)(BC) = (AC + BC)^2</math>.
  
−
Let <math>h</math> denote the height to the [[hypotenuse]] of triangle <math>ABC</math>. Notice that <math>h - \frac {1}{21}h = \sqrt {440}</math>. (The height of <math>ABC</math> decreased by the corresponding height of <math>T_5</math>) Thus, <math>(AB)(h) = (AC)(BC) = 22\cdot 21^2</math>. Because <math>AB^2 + 2(AB)(BC) = (AC + BC)^2 = 21^2\cdot22^2</math>, <math>AC + BC = (21)(22) = 462</math>.[/
+
Let <math>h</math> denote the height to the [[hypotenuse]] of triangle <math>ABC</math>. Notice that <math>h - \frac {1}{21}h = \sqrt {440}</math>. (The height of <math>ABC</math> decreased by the corresponding height of <math>T_5</math>) Thus, <math>(AB)(h) = (AC)(BC) = 22\cdot 21^2</math>. Because <math>AB^2 + 2(AB)(BC) = (AC + BC)^2 = 21^2\cdot22^2</math>, <math>AC + BC = (21)(22) = 462</math>.
  
 
== See also ==
 
== See also ==

Revision as of 09:38, 10 October 2007

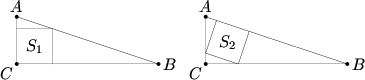
Problem

Squares $S_1$ and $S_2$ are inscribed in right triangle $ABC$, as shown in the figures below. Find $AC + CB$ if area $(S_1) = 441$ and area $(S_2) = 440$.

AIME 1987 Problem 15.png

Solution

An image is supposed to go here. You can help us out by creating one and editing it in. Thanks.

Because all the triangles in the figure are similar to triangle $ABC$, it's a good idea to use area ratios. In the diagram above, $\frac {T_1}{T_3} = \frac {T_2}{T_4} = \frac {441}{440}.$ Hence, $T_3 = \frac {440}{441}T_1$ and $T_4 = \frac {440}{441}T_2$. Additionally, the area of triangle $ABC$ is equal to both $T_1 + T_2 + 441$ and $T_3 + T_4 + T_5 + 440.$

Setting the equations equal and solving for $T_5$, $T_5 = 1 + T_1 - T_3 + T_2 - T_4 = 1 + \frac {T_1}{441} + \frac {T_2}{441}$. Therefore, $441T_5 = 441 + T_1 + T_2$. However, $441 + T_1 + T_2$ is equal to the area of triangle $ABC$! This means that the ratio between the areas $T_5$ and $ABC$ is $441$, and the ratio between the sides is $\sqrt {441} = 21$. As a result, $AB = 21\sqrt {440} = \sqrt {AC^2 + BC^2}$. We now need $(AC)(BC)$ to find the value of $AC + BC$, because $AB^2 + 2(AC)(BC) = (AC + BC)^2$.

Let $h$ denote the height to the hypotenuse of triangle $ABC$. Notice that $h - \frac {1}{21}h = \sqrt {440}$. (The height of $ABC$ decreased by the corresponding height of $T_5$) Thus, $(AB)(h) = (AC)(BC) = 22\cdot 21^2$. Because $AB^2 + 2(AB)(BC) = (AC + BC)^2 = 21^2\cdot22^2$, $AC + BC = (21)(22) = 462$.

See also

1987 AIME (Problems • Answer Key • Resources)
Preceded by
Problem 14 		Followed by
Last
Question
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1987_AIME_Problems/Problem_15&oldid=17783"