Difference between revisions of "Stewart's theorem"
Jayevvms123 (talk | contribs) (→Proof 1) |
Jayevvms123 (talk | contribs) (→Proof 1) |
||
| Line 20: | Line 20: | ||
<cmath>d^2m + d^2n = d^2(m + n) = d^2a.</cmath> | <cmath>d^2m + d^2n = d^2(m + n) = d^2a.</cmath> | ||
This simplifies our equation to yield <math>man + dad = bmb + cnc,</math> or Stewart's theorem. | This simplifies our equation to yield <math>man + dad = bmb + cnc,</math> or Stewart's theorem. | ||
| − | |||
Good Job! You mastered Stewart's Theorem. | Good Job! You mastered Stewart's Theorem. | ||
Revision as of 10:43, 24 November 2022
Contents
Statement
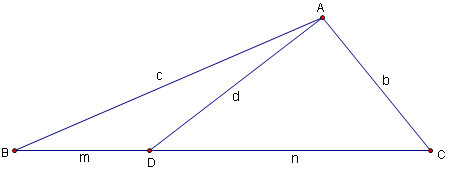
Given a triangle ![]() with sides of length
with sides of length ![]() and opposite vertices
and opposite vertices ![]() ,
, ![]() ,
, ![]() , respectively. If cevian
, respectively. If cevian ![]() is drawn so that
is drawn so that ![]() ,
, ![]() and
and ![]() , we have that
, we have that ![]() . (This is also often written
. (This is also often written ![]() , a phrase which invites mnemonic memorization, i.e. "A man and his dad put a bomb in the sink.")
, a phrase which invites mnemonic memorization, i.e. "A man and his dad put a bomb in the sink.")
Proof 1
Applying the Law of Cosines in triangle ![]() at angle
at angle ![]() and in triangle
and in triangle ![]() at angle
at angle ![]() , we get the equations
, we get the equations
Because angles ![]() and
and ![]() are supplementary,
are supplementary, ![]() . We can therefore solve both equations for the cosine term. Using the trigonometric identity
. We can therefore solve both equations for the cosine term. Using the trigonometric identity ![]() gives us
gives us
Setting the two left-hand sides equal and clearing denominators, we arrive at the equation: ![]() .
However,
.
However,
![]() so
so
![]() and
and
![]() This simplifies our equation to yield
This simplifies our equation to yield ![]() or Stewart's theorem.
or Stewart's theorem.
Good Job! You mastered Stewart's Theorem.
Proof 2 (Pythagorean Theorem)
Let the altitude from ![]() to
to ![]() meet
meet ![]() at
at ![]() . Let
. Let ![]() ,
, ![]() , and
, and ![]() . So, applying Pythagorean Theorem on
. So, applying Pythagorean Theorem on ![]() yields
yields
![]()
Since ![]() ,
, ![]()
Applying Pythagorean on ![]() yields
yields
![]()
Substituting ![]() ,
, ![]() , and
, and ![]() in
in ![]() and
and ![]() gives
gives
![]()
![]()
Notice that
![]()
![]() are equal to each other. Thus,
are equal to each other. Thus, ![]() Rearranging the equation gives Stewart's Theorem:
Rearranging the equation gives Stewart's Theorem:
![]()
~sml1809
Nearly Identical Video Proof with an Example by TheBeautyofMath
~IceMatrix









