Difference between revisions of "1988 AIME Problems/Problem 7"
(solution) |
|||
| Line 3: | Line 3: | ||
== Solution == | == Solution == | ||
| − | + | <center>[[Image:AIME_1988_Solution_07.png]]</center> | |
| − | Let <math>D</math> be the intersection of the [[altitude]] and <math>\overline{BC}</math>, and <math>h</math> be the length of the altitude. [[Without loss of generality]], let <math>BD = 17</math> and <math>CD = 3</math>. Then <math>\tan \angle DAB = \frac{17}{h}</math> and <math>\tan \angle CAD = \frac{3}{h}</math>. Using the [[tangent sum formula]], | + | Let <math>D</math> be the intersection of the [[altitude]] and <math>\overline{BC}</math>, and <math>h</math> be the length of the altitude. [[Without loss of generality]], let <math>BD = 17</math> and <math>CD = 3</math>. Then <math>\tan \angle DAB = \frac{17}{h}</math> and <math>\tan \angle CAD = \frac{3}{h}</math>. Using the [[Trigonometric_identities#Angle_Addition.2FSubtraction_Identities|tangent sum formula]], |
<div style="text-align:center;"> | <div style="text-align:center;"> | ||
Revision as of 17:47, 3 November 2007
Problem
In triangle 
, 
, and the altitude from 
divides 
into segments of length 3 and 17. What is the area of triangle ?
Solution
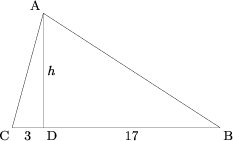
Let 
be the intersection of the altitude and 
, and 
be the length of the altitude. Without loss of generality, let 
and 
. Then 
and 
. Using the tangent sum formula,
$\begin{eqnarray*} \tan CAB &=& \tan (DAB + CAD)\\ \frac{22}{7} &=& \frac{\tan DAB + \tan CAD}{1 - \tan DAB \cdot \tan CAD} \\ &=& \frac{\frac{17}{h} + \frac{3}{h}}{1 - \left(\frac{17}{h}\right)\left(\frac{3}{h}\right)} \\ \frac{22}{7} &=& \frac{20h}{h^2 - 51}\\ 0 &=& 22h^2 - 140h - 22 \cdot 51\\ 0 &=& (11h + 51)(h - 11)
\end{eqnarray*}$ (Error compiling LaTeX. Unknown error_msg)The postive value of 
, so the area is 
.
See also
| 1988 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 6 |
Followed by Problem 8 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
