Difference between revisions of "1991 OIM Problems/Problem 6"
| Line 8: | Line 8: | ||
Case 1: <math>\angle NHM = 90^{\circ}</math> | Case 1: <math>\angle NHM = 90^{\circ}</math> | ||
| − | If you measure | + | [[File:1991_OIM_P6a.png|500px]] |
| + | |||
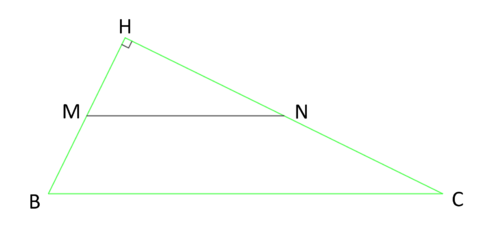
| + | If you measure <math>\angle NHM</math> on the given points and it happens to be a right angle, then constructing the triangle is easy because point <math>H</math> is also point <math>A</math> of the triangle <math>ABC</math>. One can notice if this angle is a right angle or not if you can draw a perpendicular from point <math>M</math> to line <math>NH</math> and it passes through <math>H</math>. If this happens to be the case, then since <math>AM=MB</math> and <math>AN=NC</math> then one can simply draw a circle with the compass at points <math>M</math> and <math>N</math> with radiuses measuring <math>MA</math> and <math>NA</math> respectively. Then extend the lines <math>AM</math> and <math>AN</math> to the intersection on their respective circles at <math>B</math> and <math>C</math> respectively. Then draw triangle <math>ABC</math>. | ||
| + | |||
| + | Case 2: <math>\angle NHM \ne 90^{\circ}</math> | ||
| + | |||
| + | |||
* Note. I actually competed at this event in Argentina when I was in High School representing Puerto Rico. I think I may have been able to build some cases of this. I don't remember much of it. | * Note. I actually competed at this event in Argentina when I was in High School representing Puerto Rico. I think I may have been able to build some cases of this. I don't remember much of it. | ||
Revision as of 18:10, 22 December 2023
Problem
Given 3 non-aligned points 
, 
and 
, we know that and are midpoints of two sides of a triangle and that is the point of intersection of the heights of said triangle. Build the triangle.
~translated into English by Tomas Diaz. ~orders@tomasdiaz.com
Solution
Case 1: 
If you measure 
on the given points and it happens to be a right angle, then constructing the triangle is easy because point is also point 
of the triangle 
. One can notice if this angle is a right angle or not if you can draw a perpendicular from point to line 
and it passes through . If this happens to be the case, then since 
and 
then one can simply draw a circle with the compass at points and with radiuses measuring 
and 
respectively. Then extend the lines 
and 
to the intersection on their respective circles at 
and 
respectively. Then draw triangle .
Case 2: 
- Note. I actually competed at this event in Argentina when I was in High School representing Puerto Rico. I think I may have been able to build some cases of this. I don't remember much of it.
Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.
