Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1985 AHSME Problems/Problem 14"
(Improved wording, formatting, and LaTeX)
 
Line 1: Line 1:
 
==Problem==
 
==Problem==
−
Exactly three of the interior angles of a convex [[polygon]] are obtuse. What is the maximum number of sides of such a polygon?
+
Exactly three of the interior angles of a convex polygon are obtuse. What is the maximum number of sides of such a polygon?
  
 
<math> \mathrm{(A)\ } 4 \qquad \mathrm{(B) \ }5 \qquad \mathrm{(C) \  } 6 \qquad \mathrm{(D) \  } 7 \qquad \mathrm{(E) \  }8 </math>
 
<math> \mathrm{(A)\ } 4 \qquad \mathrm{(B) \ }5 \qquad \mathrm{(C) \  } 6 \qquad \mathrm{(D) \  } 7 \qquad \mathrm{(E) \  }8 </math>
  
 
==Solution==
 
==Solution==
−
All angle measures are in degrees.
+
Suppose that such a polygon has <math>n</math> sides. Let the three obtuse angle measures, in degrees, be <math>o_1</math>, <math>o_2</math>, and <math>o_3</math> and the <math>(n-3)</math> acute angle measures, again in degrees, be <math>a_1,a_2,a_3, \dotsc a_{n-3}</math>.
  
−
The sum of the interior angle measures of an <math> n </math>-gon is <math> 180(n-2)=180n-360 </math>. Let the three obtuse angle measures be <math> o_1, o_2, </math> and <math> o_3 </math>, and the <math> n-3 </math> acute angle measures be <math> a_1, a_2, a_3, \cdots </math>.
+
Since <math>90 < o_i < 180</math> for each <math>i</math>, we have <cmath>3(90) = 270 < o_1+o_2+o_3 < 3(180) = 540,</cmath> and similarly, since <math>0 < a_i < 90</math> for each <math>i</math>, <cmath>0 < a_1+a_2+a_3+\dotsb+a_{n-3} < 90(n-3) = 90n-270.</cmath>
 +
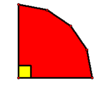
It follows that <cmath>270+0 < o_1+o_2+o_3+a_1+a_2+a_3+\dotsb+a_{n-3} < 540+90n-270,</cmath> and recalling that the sum of the interior angle measures of an <math>n</math>-gon is <math>180(n-2) = 180n-360</math>, this reduces to <math>270 < 180n-360 < 90n+270</math>. Hence <cmath>\frac{540}{180} < n < \frac{270+360}{90} \iff 3 < n < 7,</cmath> so an upper bound is <math>n \leq 6</math>, and it is easy to check that this bound can be attained by e.g. a convex hexagon with a right angle, <math>2</math> acute angles, and <math>3</math> obtuse angles, as shown below:
  
 +
[[Image: HrKCfF2ETNSQSy3uGlkg hexagonsurvey1.gif|100px]]
  
−
Since <math> 90<o_i<180 </math>, <math> 3(90)=270<o_1+o_2+o_3<3(180)=540 </math>.
+
Accordingly, the maximum possible number of sides of such a polygon is <math>\boxed{\text{(C)} \ 6}</math>.
−
 
 
−
 
 
−
Similarly, since <math> 0<a_i<90 </math>, <math> 0(n-3)=0<a_1+a_2+a_3+\cdots<90(n-3)=90n-270 </math>.
 
−
 
 
−
 
 
−
Thus, <math> 270+0<o_1+o_2+o_3+a_1+a_2+a_3+\cdots<540+90n-270 </math> <math> \implies 270<180n-360<90n+270 </math>.
 
−
 
 
−
 
 
−
Thus, <math> 180n-360<90n+270\implies n<7 </math>, so the largest possible <math> n </math> is <math> 6, \boxed{\text{C}} </math>.
 
  
 
==See Also==
 
==See Also==
 
{{AHSME box|year=1985|num-b=13|num-a=15}}
 
{{AHSME box|year=1985|num-b=13|num-a=15}}
 
{{MAA Notice}}
 
{{MAA Notice}}

Latest revision as of 20:23, 19 March 2024

Problem

Exactly three of the interior angles of a convex polygon are obtuse. What is the maximum number of sides of such a polygon?

$\mathrm{(A)\ } 4 \qquad \mathrm{(B) \ }5 \qquad \mathrm{(C) \ } 6 \qquad \mathrm{(D) \ } 7 \qquad \mathrm{(E) \ }8$

Solution

Suppose that such a polygon has $n$ sides. Let the three obtuse angle measures, in degrees, be $o_1$, $o_2$, and $o_3$ and the $(n-3)$ acute angle measures, again in degrees, be $a_1,a_2,a_3, \dotsc a_{n-3}$.

Since $90 < o_i < 180$ for each $i$, we have \[3(90) = 270 < o_1+o_2+o_3 < 3(180) = 540,\] and similarly, since $0 < a_i < 90$ for each $i$, \[0 < a_1+a_2+a_3+\dotsb+a_{n-3} < 90(n-3) = 90n-270.\] It follows that \[270+0 < o_1+o_2+o_3+a_1+a_2+a_3+\dotsb+a_{n-3} < 540+90n-270,\] and recalling that the sum of the interior angle measures of an $n$-gon is $180(n-2) = 180n-360$, this reduces to $270 < 180n-360 < 90n+270$. Hence \[\frac{540}{180} < n < \frac{270+360}{90} \iff 3 < n < 7,\] so an upper bound is $n \leq 6$, and it is easy to check that this bound can be attained by e.g. a convex hexagon with a right angle, $2$ acute angles, and $3$ obtuse angles, as shown below:

HrKCfF2ETNSQSy3uGlkg hexagonsurvey1.gif

Accordingly, the maximum possible number of sides of such a polygon is $\boxed{\text{(C)} \ 6}$.

See Also

1985 AHSME (Problems • Answer Key • Resources)
Preceded by
Problem 13 		Followed by
Problem 15
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30
All AHSME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1985_AHSME_Problems/Problem_14&oldid=217124"